当前位置：文档库 › 运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及丨、V:用习题解答

习题一 P46

1.1

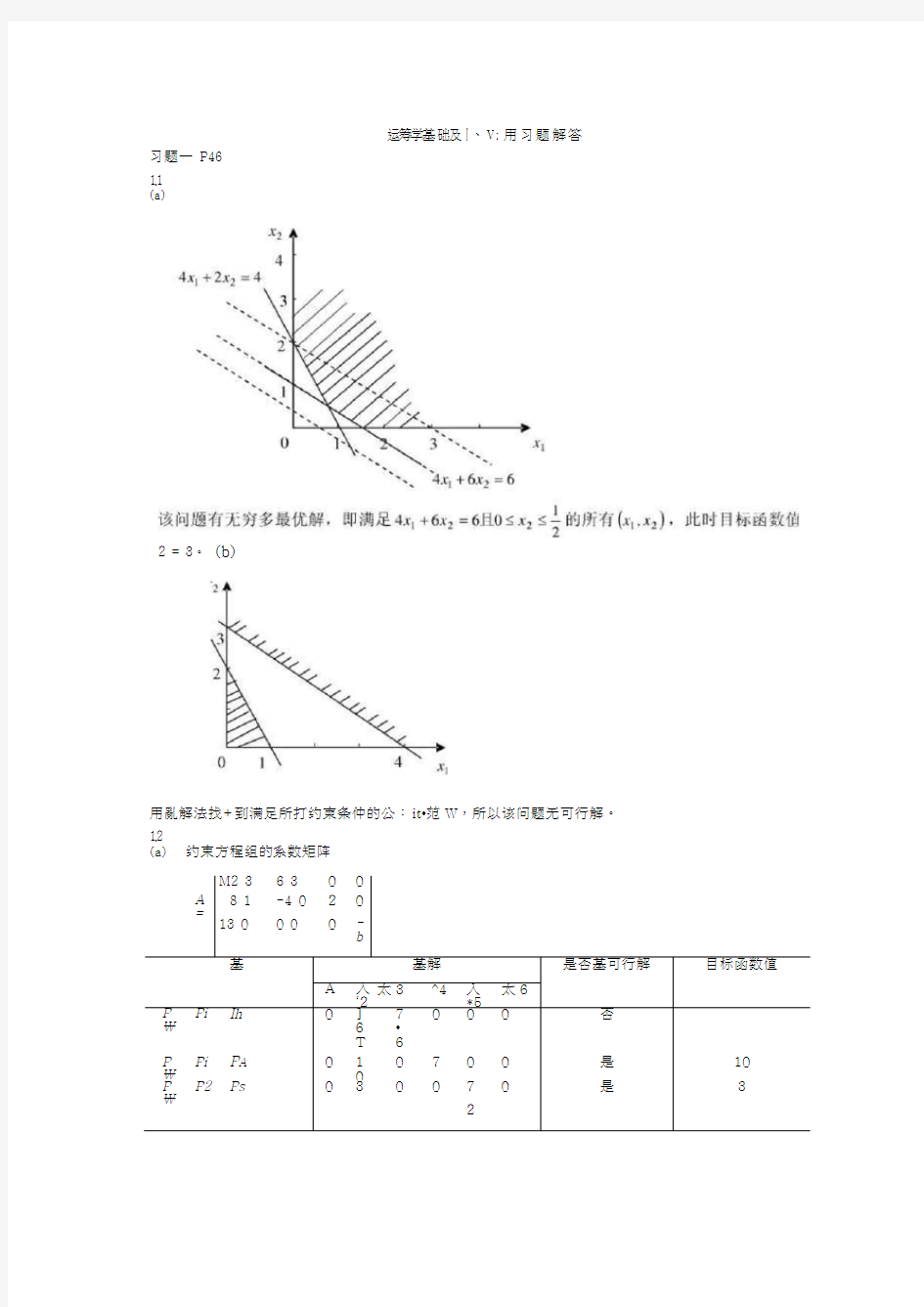
(a)

2 = 3。(b)

用亂解法找+到满足所打约柬条仲的公：it?范W，所以该问题无可行解。

1.2

(a)约束方程组的系数矩阵

最优解A.=(o，i a o,7，o，o)r

(b)约束方程组的系数矩阵 f I 2 3 4、

4 = l2 2 I 2,

最优解1 = (^,0，11，0^ V5

5 )"

1.3

(a)

(1)图解法

⑵单纯形法

首先在各约朿条件上添加松弛变铽，将问题转化为标准形式max z = 10a-, +5a'2 +0x3 +0a4

[3a-. +4 义2 + A3 = 9 si.

[5a-j + 2X2 + a'4 = 8

则A，P4组成个猫《=令 A = ;c2 = 0

得-站可行解a_ = (0.0.9,8)，山此列出初始单纯形表

cr 2 >0， 0 - minj 2A

xi =~，a-3 =0, a 4

最优解即为严+2X2

的解x =卩，2V 最大值z : I

A"i + X y =

I 2 2 /

新的单纯形农为

A', Xo X A

14 14

_5_ _25

M ~T?

q.qcO ，表明已找到问题垴优解.

(b)

(1)图解法

(2)

单

纯形法

苘先在外约朿条件.h 添加松弛变M ，将问题转化为标准形式 max z = 2.v, + x 2 + Ox 3 + 0.v 4 + Oa 5 5a'2 + = 15 6.y, + 2x 2 + .v 4 = 24

0 0

0 --

2 *^4

o A :

、Q 0 一4

(7,^2 <0,表明已找到问题最优解^ =1，X 2=- , A-3

估

? 17

Hi Z =——

1.6

(a)在约朿条件中添加松弛变量或剩余变量，且令k = jc 2 -a :； (a*2 > 0,.v ； > o)

Xx = ~X->

该问题转化为

max z' = -3a, - x 2 + .v 2 - 2a 3 + 0.v 4 + (Xv 5 2x | + 3a -2 - 3a 2

+ 4a 3 +a 4 =12

攀 M I

4a'| +x 2 -A*2 -2a*3 —^5 =8 3a*, -X 2 +X 2 — 3a*3 = 6

A*,, A '2，X 2, x 3，A-4 , A 3 ^ 0

-K 约朿系数矩陴为

3 -3

4 I 0 4 丨-1-2

0-1

3 -丨丨一3 0 0

在A 屮人为地添加两列单位向虽/>7，

2 3 -3 4 1 0 0 0 4 丨-1 -2 t) -1 丨 0 3-1 I -3 0 0 0 1

令 max z'= -3a -i - x 2 +x 2- 2.v 3 + Oa:., + 0.v 5 - Mx 6 - Mx 7 得初始单纯形表

最大

a 4 = 0，x 5

SS ^ Xi x 2

x 4 x 5 x 6

-2 0 0

M -M

4 1

0 -I 0 0

0 0 0

-3 + 7M -J 1 -2-5M 0 -M 0 0

-I

-5

(b)

在约朿条件中添加

松弛变M 或剩余变M ，.R 令a:3 (jc 3>0,.x ；>0)

该问题转化为

max z ? = 一3^ - 5.v 2 + x ?- x ? + 0,v 4 + Ox 5 x, + 2X 2 + x^- x^-x 4 =6 2.v, + x 2

- 3jc 3 - 3^：3 + a*5 = 16 x 2+ 5 a*3 一 5a*3

= 10 ?v p A ：2，

“x 4，A 5

艽约柬系数矩阵

为

13-30-1 115-50 0

ft A 屮人为地添加两列单位向觉p 7, 12

1-10

10、

2 13-30 100 115 -5 0 0 01

、 /

令 max z , = -3a*, 一 5,v 2 + .v 3 一 x 3 + 0x 4 + 0x s 一 Mx b - Mx 1

衍初始单纯形表

0 0 -M - M X. X, X,

X, X, X, X, x n

-A/ x 6

-M x 7 10

-3 + 2A/ 5 + 3M 1+6M -1-6M -M 0 0 0

(a)解1:大\1法

在上述线性规划问题中分别减去剩余变萤x 4，x 6,?再加上人工变蛩15，17，'，

得max z = 2x t - x2 + 2x3 + 0,v4 - Mx s + 0,v6 - Mx7 + 0a8- Mx^

-3 + 7M -J 1 -2-5M 0 -M 0 0

A', + X 2 + A ：3 - + JC 5 = 6 -2x l + jc 3 — a*6 + x 1 —2 2x z — j c 3 - a *8

+ j c 9 =0

a-,,.v 2,a*3,j:4,a:5,^6,x 7,x 8,a-9 >0

，

其中MS 个任意人的正数-据此可列出单纯形表

jc, x 2

x 4

5 X

6 A

-M x s 6 -M x 7

一

2 —M

a 、0

0 0 0

[2]

0 M 0

2-M 3A/-1 2 + A/ -M 1/2 -1/2 0 0

1/2 -1/2

x s

-M x,

—I

x\ [1]

1/2

^ 5M 3 … ^

… A/ I 1 3A/ 2-M

0 ----- + — - M

0 -M 0 ------------------ 一十 ---

2 2 2 2 2 2

-M jr 5 3 2 .v 3 2 -I x 2 I 3/2 -3/2 1/2 -1/2 -

-1/2 1/2 -1/2 1/2

0 0 0 1 1 0

3/4

0 0

?>M +3 -5M -3 M

-3M

4Af+5 0 ■M

2 2

x, 3/4 A 3 7/2 7/4

0 0

0 1 0

| 4

3/8 - 8 8

-5/4 -M

山单纯形表计算结果可以ft 出，ct 4 >0且％<0(/ =丨，2，3),所以该线性规划问题有无界解解

两阶段法。

现在.卜.述线性规划问题的约柬条件『I *分別减去剩余变觉，x (、, a 8，再加上人丨:变鼠

x^x^x^nm ?阶段的数学模型

据此可列出单纯形表

-5/2

第阶段求得的最优解)^=(^0，0，0，0,0，0)'|:1标函数的最优值‘=0。

4 4 2

因人工变jfU 5 =x 7 =% =0，所以A^(m ，0,0，0，0,0，0)T

^原线性规划问题的骓可

行解。于是可以进行第阶段运箅。将第-?阶段的最终表屮的人:丨:变獄取消,并填入原问题的目标函数的

[2]

尤

一

A 1

0 0 尤

-1

久

X 7

0 0

3/2

[1]

1/2

-1

0 义.

A -7

1/2 -1/2 0 0

1/2 -1/2

0 0

0 0 0 1 I 0

3/2 -3/2 1/2 -1/2 一I

丨 0 0 -1/2 1/2 -1/2 1/2

3/4

X , 3/4

A -3

7/2 x 2 7/4

0 0

现在上述线性规划问题的约朿条件屮分别减去剩余变觉a-4,;c 5,再加上人丨:变母a-6，a -7，

得第

-M

[4J

由表中计尊结果可以肴出，a 4>0 P l ?<0(/ = 1，2，3)，所以原线性.规划问题苻无界解。 (b )

解1：大M 法

在上述线性规划问题中分別减去剩余变虽x 4,;r 6，A ，再加上人丨:变:6Lr 547，\，得 min z = 2jc, + 3x 2 + a*3 + 0.v 4 + 0a*5 + Mx b - Mx n

jc, + 4a*2 + 2jc 3 一 x 4 += 3a*, + 2X 2 -

x s + x 7 = 6

.A|，-'2，-'3，-^4，?^5 , ，-'8 > -^*y — ^

其中M 是个任意大的正数。据此可列出单纯形表

■

c#基办

M x 6 8 M x 7

2-AM 3-6M I -2M

1/2 1/2 M-M2 Af-1/2

山单纯形表计算结果可以f h h.最优解欠’=(|,|，0，0,0，0，0/ , 1=1标函数的垴优解值

z* =2x l + 3x | = 7。父存在非《变萤检验数c r 3 = 0,故该线性规划问埋Y f 无穷多鍛优解《解2:两阶段法。

1/4 1 [5/2] 0

1/2

-1/4 1/2 1/4

-1/2

5 X

2 M x n

3 \M

-M 0 M

3/5 -2/5

-3/10 1/10 3/10 一 1/10 x 2

9/5

a :, 4/5

1/5

-2/5 -1/5 2/5

x 2 9/5 a *. 4/5

?阶段的数学模耶min 似:

jc, + 4X 2 + 2x 3 一 a*4 + jc 6 = 8 3.v,

+ 2X 2 -x s + jc 7 =6

,v ,，，A ”v 5，A ，a.7，A ”v y > 0 据此可列出单纯形表

3/5 -3/10 1/10 3/10 -1/10 -2/5 1/5

-2/5 -1/5 2/5

第阶段求得的最优解又^^…………別^行标函数的最优值^； =0。

丨入1人:1:变跫jc 6=a> =0，所以（H ，0，0,0，O’O)1■?足原线性规划问题的骓可行解。于足可

以进行第：：阶段运箅。将第?阶段的最终表屮的人工变M 取消，井填入原问题的R 标函数的系数，进行第.：阶A .2

[4]

A X

6 0

2 3

-4 -6

1/4 1 [5/2]

1/4

1/2

1/2 -1/4

-1 1/2

8 4/5

JV 2

-5/2

1/2

3/2

^=2x - + 3x - = 7?山于存在非基变罱检验数q = 0，故该线性规划问题荷无穷多最优 5 5 3

解。 1.8

0 A-6 89/15 [41/15] 0 0 -2/15 -4/5

11/15

^ = 5^,+3.v 2+8y 3 >,i

一.V 2+4y 3 =5 2y, +5.v 2+7.y 3 ^6 2>-,->'2+3>*3^3 >、无约束,>‘2

^0,>'3 ^0

-17/15 -4/5

习题二 P76 2.1 写出对偶问题

(a)

min z = 2a -! + lx 2 + 4a 3 +

3a 2 + 4jc 3 > 2 2.v t + x 2 + 3.v 3

+ y 4 < 3 + 4x 2 + 3A -

3 = 5

Aj,a-2之0，.v 3无约朿

max w =

2y { +3.V 2 +5y 3 .Vi + 2.V 2 +y 3 <2 对偶 M

题为： 3_y, + y 2 + 4v 3

< 2

4y,+3.v 2+3.y 3=4 v, >

0, v 2 < 0, >‘3无约束

max z = 5a*, + 6x 2 + 3a*3 m

.v, + 2X 2 + 2X 3 = 5

-a, + 5a 2 -jc 3 ^3

对偶问题为：

4a 、+ lx 2 + 3jc 3 < 8

无约束，jc 2 ^0,a 3 SO

2.2

(3)错误。原问题存在可行解，对偶问题可能存在可行解，也可能无可行解。

(b}错误。线性规划的对偶问题无可行解，则原问题可能无可行解，也可能为无界解4

(d>正确。

2.6对偶单纯形法 (a)

min z = 4a 、+12x 2 + I 8.V 3 + 3.V 3 > 3 sJ. <

2x 2 + 2a 3 > 5 A i

，尤2，久3 - 0

解：先将问题改W 为求Plfe 函数极人化，并化为标准形式

max z'= -4aj -12.v 2 -18x 3 十 0jc 4 +0a 5

S J .

min z 二 5a -

, + 2义2 + 4jc 3

3A _, +A -2 + 2A _3 > 4 < 6.Vj +3a 2 +5a'3 > 10

A*,.A ：2.A3 ^ 0

解：先将问题改h 为求Mfe 函数极人化，并化为称准形式

-Xi -3a-3 +x 4 : -2a'2 -

2jc 3 + ;c 5 A f >0(i = 1，.”，5)

最优解为A‘= 0，丨

目标值Z =39

max z'= -5jc, -2a: 2 - 4.v 3 +0^4 +0a 5 -3a ?丨 _ JC 2 _ 2A'3 +

m a x SJ.

c B 基b

最优解为A = (ao ，2f ， R 标值z = 8

2.8 将该问题化为标准形式：

=2.V, — A-2 +A-3 +Ojf4

+0A5,+A'2++

x4=6-A*, +2x2+

a*5=4A/ ^ 0(/ = l, -.5)

A：, x2Jl'3 A4 .V*5

V 5

山于

i < 0，

所以己找到最优解X * = (6,0,0,0,10)，

n 标函数侦^=12

(a) 令目标函数

max z = (2 + 4) x { +(-i +/l 2) x 2+C 1+/1,) x i

《1)令;^ = 4 = 0，将;反映到最终单纯形表屮

1+^3 0 0

l X 2 A

?V .

0 3

2 0

表屮解为最优的条件：4 -丨幺0 ,从而;13 < 1

表中解为最优的条件：-3 -'幺0，-1 - ^ 0? — 2

- A j < 0?从i f u A , > — 1 ⑵令 ' =毛=0，将;^反映到

最

终

单

纯

形

表

中

s.t

6+A, 10 + '0，从而;^>-6

(b)令线性规划问题为

max z = 2x{ -x2-\- x3at,

+ a:2 + a:3 < 6 + X A

—A*, + 2a*2 < 4 + A5

x^0(i = l,-3)

(l)先分析的变化

. , f1O Y A,

Ab =B-]Ab=1

使M题最优站>f、变的条件圮/T +Al/

(2)同理有

10 + A2

(c)山于Z 二（6,0，0，0，丨0)代入-&+2;v3 =~6<2，所以将约朿条件减去剩余变爾后的方程-;r, + 2x, - x6 = 2直接反映到最终单纯形表中

丨利此增加约朿条件后，新的锒优解为

10 8 22

x t =一，i 3 = ;，x 5 =一.最仇m 为

2.12

(a )线性规划问题

max z = 3^| +.v 2 +4a*3

6.V, +3^2 + 5a*3 < 45 SJ . 3.v, + A X 2 + 5a-3 ^ 30

?v.,A',,a -, ^0

单纯形法求解

运筹学参考文献

参考文献 [1] 胡运权．运筹学教程．北京：高等教育出版社，2005 [2] 胡运权．运筹学基础及应用．哈尔滨：哈尔滨工业大学出版社，1998 [3] 《运筹学》编写组．运筹学．北京：清华大学出版社， 1990 [4] 张莹．运筹学基础．北京：清华大学出版社，2002 [5] 袁亚湘，孙文瑜．最优化理论与方法．北京：科学出版社，1999 [6] 何坚勇．运筹学基础．北京：清华大学出版社， 2000 [7] 马振华等．现代应用数学手册—运筹学与最优化理论卷．北京：清华大学出版社，2000 [8] 牛映武．运筹学．西安：西安交通大学出版社，1993 [9] 梁工谦．运筹学- 典型题解析集自测试题。西安：西北工业大学出版社，2002 [10] 徐永仁．运筹学试题精选与答题技巧．哈尔滨：哈尔滨工业大学出版社，2000 [11] 徐玖平，胡知能，王緌．运筹学(第二版)．北京：科学出版社，2004 [12] 刘满风，傅波，聂高辉．运筹学模型与方法教程- 例题分析与题解．北京：清华大学出版社，2001 [13] 胡运权．运筹学习题集．北京：清华大学出版社，2002 [14] 盛昭瀚，朱乔，吴广谋．DEA理论、方法与应用．北京：科学出版社，1996 [15] Frederick ~S．Hillier，Gerald~J．Lieberman．Introduction to Operations Research (6th Ed．)．Beijing：China Machine Press/ McGraw - Hill，1999 [16] J．D．Wiest，F．K．Levy．统筹方法管理指南．北京：机械工业出版社，1983 [17] 王元等．华罗庚科普著作选集．上海：上海教育出版社，1984 [18] 江景波等．网络计划技术．北京：冶金工业出版社，1983 [19] David R．Anderson，Dennis J．Sweeney，Thomas A．Williams．数据、模型与决策．北京：机械工业出版社，2003 [20] Frederick S．Hillier，Mark S．Hillier，Jerald J．Lieberman．Introduction to Management Science．Beijing：McGraw - Hill Comanies，Inc．，2001

运筹学教案(胡运权版)

《绪论》（2课时）【教学流程图】运筹学运筹学与数学模型的基本概念管理学布置作业【教学方法】本课主要采用任务驱动和程序式思维相结合的教学方法，过程当中辅以案例讲解、启发提问、自主学习和协作学习等方式。任务驱动是实现本课教学目标和完成教学内容的主要方法，任务是师生活动内容的核心，在教学过程中，任务驱动被多次利用。自主学习能提高学生的自主探究能力，竞赛和协作学习调动学生的积极性，激发学生参与的热情。学生之间互帮互助，共同分享劳动果实，从而激发了学生的团队意识，达到理想的教学效果。【教学内容】一、教学过程：（一）举例引入：（5分钟）（1）齐王赛马的故事（2）两个囚犯的故事导入提问：什么叫运筹学？（二）新课：

绪论一、运筹学的基本概念（用实例引入）例1-1战国初期，齐国的国王要求田忌和他赛马，规定各人从自己的上马、中马、下马中各选一匹马来比赛，并且说好每输一匹马就得支付一千两银子给予获胜者。当时齐王的马比田忌的马强，结果每年田忌都要输掉三千两银子。但孙膑给田忌出主意，可使田忌反输为赢。试问：如果双方都不对自己的策略保密，当齐王先行动时，哪一方会赢？赢多少？反之呢？例1-2有甲乙两个囚犯正被隔离审讯，若两人都坦白，则每人判入狱8年；若两个人都抵赖，则每人判入狱1年；若只有一人坦白，则他初释放，但另一罪犯被判刑10年。求双方的最优策略。乙囚犯抵赖坦白甲囚犯抵赖 -1，-1 -10，0 坦白 0，-10 -8，-8 定义：运筹学（Operation Research）是运用系统化的方法，通过建成立数学模型及其测试，协助达成最佳决策的一门科学。它主要研究经济活动和军事活动中能用数学的分析和运算来有效地配置人力、物力、财力等筹划和管理方面的问题。二、学习运筹学的方法 1、读懂教材上的文字；

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用习题解答 z 3。 (b) 用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。 (a)约束方程组的系数矩阵 12 3 6 3 0 A 8 1 4 0 2 3 0 0 0 0 基基解是否基可行解目标函数值 X1 X2 X3 X4 X5 X6 P1 P2 P3 16 3 7 -6 0 0 0 否 P1 P2 P4 0 10 0 7 0 0 是10 P1 P2 P5 0 3 0 0 7 2 是 3 习题一P46 x i 1 -的所有X i,X2，此时目标函数值

o (b)约束方程组的系数矩阵 A 12 3 4 A 2 2 12 ⑻ (1)图解法基基解是否基可行解目标函数值 X 1 X 2 X 3 X 4 P 1 P 2 4 11 否 "2 P 1 P 3 2 0 11 0 是 43 5 ~5 ~5 P 1 P 4 1 11 否 — 3 6 P 2 P 3 1 2 是 5 2 P 2 P 4 1 否 2 2 P 3 P 4 0 0 1 1 是 5

max z 10x 1 5x 2 0x 3 0x 4 3x i 4X 2 X 3 st. 5x 1 2x 2 x 4 8 9 8 1 2。 min —,— — 5 3 5 C j 10 5 0 0 C B 基 b X 1 X 2 X 3 X 4 21 14 3 0 X 3 — 1 — "5" 5 5 8 2 1 10 X 1 1 C j 10 5 0 0 C B 基 b X 1 X 2 X 3 X 4 0 X 3 9 3 4 1 0 0 X 4 8 [5] 2 0 1 C j Z j 10 5 令 X i X 2 0,0,9,8，由此列出初始单纯形表最优解即为3x1 4x2 9的解x 5x 1 2x 2 8 1,-，最大值z 竺 2 2 (2)单纯形法首先在各约束条件上添加松弛变量, 将问题转化为标准形式则P 3，P 4组成一个基。得基可行解x

运筹学(胡运权)第五版课后答案-运筹作业

47页1.1b 用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解47页1.1d 无界解 1 2 3 4 5 4 3 2 1 - 1 -6 -5 -4 -3 -2 X2 X1 2x1- -2x1+3x 1 2 3 4 4 3 2 1 X1 2x1+x2=2 3x1+4x2= X

1.2（b）约束方程的系数矩阵A= 1 2 3 4 2 1 1 2 P1 P2 P3 P4 基基解是否可行解目标函数值X1 X2 X3 X4 P1 P2 -4 11/2 0 0 否 P1 P3 2/5 0 11/5 0 是43/5 P1 P4 -1/3 0 0 11/6 否 P2 P3 0 1/2 2 0 是 5 P2 P4 0 -1/2 0 2 否 P3 P4 0 0 1 1 是 5 最优解A=(0 1/2 2 0)T和(0 0 1 1)T 49页13题设Xij为第i月租j个月的面积 minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x1 3 +6000x23+7300x14 s.t. x11+x12+x13+x14≥15 x12+x13+x14+x21+x22+x23≥10 x13+x14+x22+x23+x31+x32≥20 x14+x23+x32+x41≥12 Xij≥0 用excel求解为： ( )

用LINDO求解： LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION V ALUE

运筹学基础及应用课后习题答案

运筹学基础及应用习题解答习题一 P46 (a) 该问题有无穷多最优解，即满足2 1 0664221≤≤=+x x x 且的所有()21,x x ，此时目标函数值3=z 。 (b) 用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。 (a) (1) 图解法

最优解即为?? ?=+=+82594321 21x x x x 的解??? ??=23,1x ，最大值235=z (2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 ???=++=+++++=8 25943 ..00510 max 421321 4321x x x x x x t s x x x x z 则43,P P 组成一个基。令021==x x 得基可行解()8,9,0,0=x ，由此列出初始单纯形表 21σσ>。5 839,58min =?? ? ??=θ

02>σ，23 28,1421min =??? ? ?=θ 0,21<σσ，表明已找到问题最优解0 , 0 , 2 3 1,4321====x x x x 。最大值 2 35 *=z (b) (1) 图解法 \\ 最优解即为?? ?=+=+5 24262121x x x x 的解??? ??=23,27x ，最大值217=z (2) 单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式

1234523124125 max 2000515.. 6224 5z x x x x x x x s t x x x x x x =+++++=?? ++=??++=? 则3P ，4P ，5P 组成一个基。令021==x x 得基可行解()0,0,15,24,5x =，由此列出初始单纯形表 21σσ>。245min ,,461θ? ?=-= ?? ? 02>σ，15 33min ,24,5 22θ??== ??? 新的单纯形表为

运筹学(胡运权版)第三章运输问题课后习题答案

P66： 8.某部门有3个生产同类产品的工厂（产地），生产的产品由4个销售点出售，各工厂A 1， A 2，A 3的生产量、各销售点B 1，B 2，B 3，B 4的销售量（假定单位为t ）以及各工厂到销售点的单位运价（元/t ）示于下表中，问如何调运才能使总运费最小？表解：一、该运输问题的数学模型为：可以证明：约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6. 34 33323124232221 3141 141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++== ∑∑ ==??? ??????????==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,0141214822 1016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111??? ? ? ? ? ? ? ? ? ???

二、给出运输问题的初始可行解（初始调运方案） 1. 最小元素法思想：优先满足运价（或运距）最小的供销业务。

其余（非基）变量全等于零。此解满足所有约束条件，且基变量（非零变量）的个数为6（等于m+n-1=3+4-1=6). 总运费为（目标函数值） ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===314 1 i j ij ij x c Z

运筹学基础及应用第四版胡运权主编课后练习答案

GAGGAGAGGAFFFFAFAF 運籌學基礎及應用習題解答習題一 P46 1.1 (a) 該問題有無窮多最優解，即滿足2 10664221≤≤=+x x x 且的所有()21,x x ，此時目標函數值3=z 。 (b) 用圖解法找不到滿足所有約束條件的公共范圍，所以該問題無可行解。 4

GAGGAGAGGAFFFFAFAF 1.2 (a) 約束方程組的系數矩陣 ???? ? ??--=1000030204180036312A 最優解()T x 0,0,7,0,10,0=。 (b) 約束方程組的系數矩陣 ? ?? ? ??=21224321A

GAGGAGAGGAFFFFAFAF 最優解T x ? ?? ??=0,511,0,5 2。 1.3 (a) (1) 图解法

GAGGAGAGGAFFFFAFAF 最優解即為? ? ?=+=+8259432 1 21x x x x 的解?? ? ??=2 3,1x ，最大值235=z (2)单纯形法首先在各約束條件上添加松弛變量，將問題轉化為標準形式 ???=++=+++++=8 259 43 ..00510 max 421321 4321x x x x x x t s x x x x z 則43,P P 組成一個基。令021==x x 得基可行解()8,9,0,0=x ，由此列出初始單純形表

GAGGAGAGGAFFFFAFAF 21σσ>。5 839,58min =?? ? ??=θ 02>σ，2 328,1421min =??? ?? =θ 新的單純形表為

运筹学[胡运权]第五版课后答案,运筹作业

运筹学[胡运权]第五版课后答案,运筹作业 -标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII

47页1.1b 用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解47页1.1d 无界解

1.2（b）约束方程的系数矩阵 A= 1 2 3 4 ( ) 2 1 1 2 P1 P2 P3 P4 最优解A=(0 1/2 2 0)T和(0 0 1 1)T 49页13题设Xij为第i月租j个月的面积 minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13 +6000x23+7300x14 s.t. x11+x12+x13+x14≥15 x12+x13+x14+x21+x22+x23≥10 x13+x14+x22+x23+x31+x32≥20 x14+x23+x32+x41≥12 Xij≥0 用excel求解为：

用LINDO求解： LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION VALUE 1) 118400.0 VARIABLE VALUE REDUCED COST Z 0.000000 1.000000 X11 3.000000 0.000000

X21 0.000000 2800.000000 X31 8.000000 0.000000 X41 0.000000 1100.000000 X12 0.000000 1700.000000 X22 0.000000 1700.000000 X32 0.000000 0.000000 X13 0.000000 400.000000 X23 0.000000 1500.000000 X14 12.000000 0.000000 ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 -2800.000000 3) 2.000000 0.000000 4) 0.000000 -2800.000000 5) 0.000000 -1700.000000 NO. ITERATIONS= 3 答若使所费租借费用最小，需第一个月租一个月租期300平方米，租四个月租期1200平方米，第三个月租一个月租期800平方米，

运筹学基础及应用

运筹学基础及应用 P43例13 、混合配料问题:某糖果厂用原料A、B、C加工成三种不同牌号的糖果甲、乙、丙。已知各种牌号糖果中A、B、C含量，原料成本，各种原料的每月限制用量，三种牌号糖果的单位加工费及售价如表1-19所示。问该厂每月生产这三种牌号糖果各多少千克，使该厂获利最大。试建立这个问题的线性规划的数学模型。表1-19 甲乙丙原料成本(元/kg) 每月限制用量(kg) A 2.00 2000 ?60% ?30% B 1.50 2500 C 1.00 1200 ?20% ?50% ?60% 0.50 0.40 0.30 加工费(元/kg) 3.40 2.85 2.25 售价(元/kg) P44例14、投资项目的组合问题:兴安公司有一笔30万元的资金，考虑今后三年内用于下列项目的投资: (1) 三年内的每年年初均可投资，每年获利为投资额的20%，其本利可一起用于下一年投资; (2) 只允许第一年初投入，于第二年末收回，本利合计为投资额的150%，但此类投资限额不超过15万元; (3) 允许于第二年初投入，于第三年末收回，本利合计为投资额的160%，但限额投资20万元; (4) 允许于第三年初投入，年末收回，可获利40%，但限额为10万元。试为该公司确定一个使第三年末本利和为最大的投资组合方案。 P44例15、生产、库存与设备维修综合计划的安排:红光厂有2台车床，1台钻床，1台磨床，承担4中产品的生产任务(已知生产各种产品所需的设备台时及生

产单位产品的售价如表,,20所示(对各种产品今后三个月的市场最大需求(小于最大需求量时即可全部销出)及各产品在今后三个月的生产成本分别如表1,21和表1,22所示( 上述设备在1~3月内各需进行一次维修,具体安排为:2台车床于2月份、3月份各维修一台,钻床安排在2月份维修,磨床安排在3月份维修.各设备每月工作22天.每天2班,每班8h,每次维修占用半各月时间.又生产出来的产品当月销售不出去(超过最大需求量)时,可在以后各月销售,但需付每件每月储存费5元.但规定每月底各种产品储存量均不得超过100件.1月初各产品无库存,要求3月底各产品均库存50件.试安排该厂各月的生产计划,使总的利润为最大. 表,,20 a值单位:h ij i ? ? ? ? j 车床 ,., ,., ,., 钻床 ,., ,., ,., 磨床 ,., ,., ,., 售价(元,件) ,, ,, ,, ,, 表 1,21 最大需求量单位:件 K ? ? ? ? j 1月 200 300 200 200 2月 300 200 0 300 3月 300 100 400 0 表,,22 产品成本单位:元,件 K ? ? ? ? j ,月 ,, ,, ,, ,, ,月 ,, ,, ,, ,, ,月 ,, ,, ,, ,, P81例1、某食品公司经销的主要产品之一是糖果。它下面设有三个加工厂，每天的糖果生产量分别为:A1—7t,A2—4t,A3—9t.该公司把这些糖果分别运往四个地区的门市部销售，各地区每天的销售量为:B1—3t,B2—6t,B3—5t,B4—6t.已知

胡运权习题及答案(1)

习题 1.2将线性规划问题化为标准形式 st.??? ??≥≤≤-+-=++-+-=0 ,0624322min 21 321321321x x x x x x x x x x x z 解：令,' 11x x -=' " 3' 33,z z x x x -=-= 则所求规划的标准形式为： st.???? ?≥≥≥≥≥≥=++-+=+-++?+?-+-+=0 ,0,0,0,0,062403322max 54"3'32'1 5" 3'32'14" 3'32'15 4" 3'32'1'x x x x x x x x x x x x x x x x x x M x x x x z 1.4用单纯形法求解线性规划问题： st.??? ??≥≥≤+≤++=0 ,08259 43510max 21 212121x x x x x x x x z 解：将其化为标准形式为： st.?????≥≥≥≥=++=+++=0 ,0,0,08259532max 4321 4 213 212 1x x x x x x x x x x x x z 用单纯形法求解的过程见下表

故所求惟一最优解为：.2 117 max ,2 3,121== =z x x 10.1 设0X 是线性规划问题0,,max ≥==X b AX CX z 的最优解。若目标函数中用* C 代替C 后，问题的最优解变为*X 。求证：0))((0 ≥--* *X X C C 。证明：0 X 、* X 在目标函数的系数变化之前之后都是问题的可行解，故有* ≥CX CX 0 ，即 0)(, 0)(0 ≥--≥-** X X C X X C （1）同理 ,0 X C X C * * * ≥ 即 0)(0 ≥-* * X X C （2）（1）+（2） 0)()(0 ≥---* * * X X C X X C 即 .0))((0 ≥--* * X X C C 13.1某饲养场饲养动物出售，设每头动物每天至少需要700克蛋白质、30克矿物质、100毫克维生素。现有五种饲料可供选用，各种饲料每kg 营养成分含量及单价如表所示：要求确定既满足动物生长的营养需要，又使费用最省的选用饲料的方案。（仅建模型）解：设)5,4,3,2,1(=i x i 分别代表5种饲料的采购数，则模型为： st. ??? ?? ? ?=≥≥++++≥++++≥++++++++=.5,4,3,2,1,01008.022.05.030 5.022.05.0700 186238.03.04.07.02.0min 5432154321543215 4321i x x x x x x x x x x x x x x x x x x x x x z i

第五版运筹学基础与应用-大题模拟试题及答案

计算题一一 1. 下列线性规划问题化为标准型。（10分） mi nZ x-|+5x 2-2x 3 min Z 4为 2x 2+3x 3 4x ,+5x 2 6X 3=7 8% 9x 2 10x 3 11 12% 13x 2 14 X 1 0,X 2 无约束，X 3 B1 B2 B3 B4 产量 A1 10 6 7 12 4 16 10 & 9 9 A3 5 4 10 10 4 销S 5 2 4 6 i （i 1,2,3）的投资额为x 时，其收益分别为 g 1（x 1） 4禺4区） g （x 3） 2x3 ，问应如何分配投资数额才能使总收益最大？（15分） 5.求图中所示网络中的最短路。（15分）计算题二 X 1 X 2 X 3 6 2x 1 X 2 3x 3 5 X 1 X 2 10 X 1 0,X 2 0,X 3符号不限满足〈 2. 写出下列问题的对偶问题（10分） 9x 2,

5.某项工程有三个设计方案。据现有条件，这些方案不能按期完成的概率分别为 0.5,0.7,0.9, 1某工厂拥有 A,B,C 三种类型的设备，生产甲、乙两种产品，每件产品在生产中需要使用的机时数，（2）利用单纯形法求最优解；（15分） 2、用对偶理论判断下面缰性规划是否存在最优解：〔10分）屮 maxz = 2孔 +2x 3 * 满足： J 対+ 2皿叫 3. 判断下表中的启案能否作为恚上作业法求解运输间题的初始启宪，说朋理由.ho 分 n 4.如图所示的单行线交通网，每个弧旁边的数字表示这条单行线的长度。现在有一个人要从V l 出发，经过这个交通网到达 V8，要寻求使总路程最短的线路。（15分） ■.■'2 1

胡运权习题及答案习题解答(6)

习题解答（6） 1．证明：序列7、6、5、4、3、2不可能是某个简单图的次的序列。证明：由定理1有 q v d v v 2)(=∑∈，而在此序列中，∑∈v v v d )(27= 为奇数，所以此序列不可能是某个简单图的次的序列。 2．已知九个人921,,v v v 中1v 和两个人握过手，32,v v 各和四个人握过手，7654,,,v v v v 各和五个人握过手，98,v v 各和六个人握过手，证明从这九个人中一定可以找出三个人互相握过手。证明：该问题可以表述为一个9点（代表9个人）的简单图问题，不存在重复边和环，则由题意知，5)()()()(,4)()(,2)(7654321=======v d v d v d v d v d v d v d ， .6)()(98==v d v d 其中],[j i v v 表示i v 和j v 握过手。对9v 而言，因,6)(9=v d 所以7654,,,v v v v 中至少有两点存在与9v 的连线。设该两点为4v 和5v ，假设4v 和9v 相联的其它5点之间无边，则,358)(4=-≤v d 这与已知 5)(4=v d 相矛盾。故假设不成立，即4v 与上述5点间必存在至少两条边，设其中一点为k v ，则k v ， 94,v v 两两相连，即存在三人互相握过手。 3．已知下图表示7个城市间抑修建一条连接各个城市的通信线路，各边的权数表示两个城市之间线路的修建费。利用“丢边破圈法”，求连接个城市通信线路最小修建费用方案。 F 50 E B 23 C 解：在上图中依次去掉GD （6），GC （52），EF （50），AF （48），BG （46）AG （45）各边

运筹学课后习题答案

第一章线性规划1、由图可得：最优解为 2、用图解法求解线性规划： Min z=2x1+x2 ? ? ? ? ? ? ? ≥ ≤ ≤ ≥ + ≤ + - 10 5 8 24 4 2 1 2 1 2 1 x x x x x x 解：由图可得：最优解x=1.6,y=6.4

Max z=5x 1+6x 2 ? ?? ??≥≤+-≥-0 ,23222212 121x x x x x x 解：由图可得：最优解Max z=5x 1+6x 2, Max z= +∞

Maxz = 2x 1 +x 2 ????? ? ?≥≤+≤+≤0,5242261552121211x x x x x x x 由图可得：最大值?????==+35121x x x ，所以?????==2 3 21x x max Z = 8.

12 12 1 2 5.max23 28 416 412 0,1,2 maxZ. j Z x x x x x x x j =+ ?+≤ ? ≤ ? ? ≤ ? ?≥= ? 如图所示，在（4，2）这一点达到最大值为2 6将线性规划模型化成标准形式： Min z=x1-2x2+3x3 ? ? ? ? ? ? ? ≥ ≥ - = + + - ≥ + - ≤ + + 无约束 3 2 1 3 2 1 3 2 1 3 2 1 ,0 ,0 5 2 3 2 7 x x x x x x x x x x x x 解：令Z’=-Z,引进松弛变量x4≥0，引入剩余变量x5≥0，并令x3=x3’-x3’’,其中x3’≥0,x3’’≥0 Max z’=-x1+2x2-3x3’+3x3’’ ? ? ? ? ? ? ? ≥ ≥ ≥ ≥ ≥ ≥ - = + + - = - - + - = + - + + ,0 ,0 '' ,0 ' ,0 ,0 5 2 3 2 '' ' 7 '' ' 5 4 3 3 2 1 3 2 1 5 3 3 2 1 4 3 3 2 1 x x x x x x x x x x x x x x x x x x x

运筹学(胡运权)第五版课后答案,运筹作业

47页1.1b 用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解47页1.1d 无界解

1.2（b）约束方程的系数矩阵A= 1 2 3 4 ( ) 2 1 1 2 P1 P2 P3 P4 最优解A=(0 1/2 2 0)T和(0 0 1 1)T 49页13题设Xij为第i月租j个月的面积 minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13 +6000x23+7300x14 s.t. x11+x12+x13+x14≥15 x12+x13+x14+x21+x22+x23≥10 x13+x14+x22+x23+x31+x32≥20 x14+x23+x32+x41≥12 Xij≥0 用excel求解为：

用LINDO求解： LP OPTIMUM FOUND A T STEP 3 OBJECTIVE FUNCTION V ALUE 1) 118400.0 VARIABLE V ALUE REDUCED COST Z 0.000000 1.000000 X11 3.000000 0.000000

运筹学胡运权部分课后习题答案

第一章 P43-1.1（1）当取A （6/5,1/5）或B （3/2,0）时，z 取最小值3。所以该问题有无穷多最优解，所有线段AB 上的点都是最优解。 P43-1.2(1) 令' '4'44x x x -=，z z -=' ' '4'4321'55243max x x x x x z +-+-= ,,,,,,2 3214 2222465''4'43216''4 ' 43215''4'4321''4'4321≥=-+-++-=+-+-+=-+-+-x x x x x x x x x x x x x x x x x x x x x x x x P43-1.4(1) 图解法： A(0,9/4)，Z 1=45/4；B(1,3/2)，Z 2=35/2；C(8/5,0)，Z 3=16。

单纯形法：依次相当于：原点；C；B。P44-1.7(1)

无界解。两阶段法：阶段二：

P45-1.10 证明：CX (0)>=CX*，C*X*>=C*X (0) CX (0)-CX*+C*X*-C*X (0)>=0，即(C*-C)(X*-X (0))>=0。 P45-1.13 设饲料i 使用x i （kg ），则 543218.03.04.07.02.0m in x x x x x z ++++= s.t. 7001862354321≥++++x x x x x 305.022.05.054321≥++++x x x x x 1008.022.05.054321≥++++x x x x x 0,,,,54321≥x x x x x 第二章 P74-2.1(1) 321532m ax y y y w ++= 22321≤++y y y 243321≤++y y y 4334321=++y y y 无约束321,0,0y y y ≤≥

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用习题解答习题一P46 1.1 ⑻ |X2和 4 ， 4x i 2X2 4 4x i 6x2 6 1 该问题有无穷多最优解，即满足4x i 6X2 6且0 X2 ?的所有x1,x2，此时目标函数值z 3。 (b) 用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。 1.2 (a)约束方程组的系数矩阵 12 3 6 3 0 0 A 8 1 4 0 2 0 3 0 0 0 0 1

最优解x 0,10,0,7,0,0 (b)约束方程组的系数矩阵 12 3 4 A 2 2 12 T 最优解x 2,0,11,0 5 5 1.3 ⑻ (1)图解法

最优解即为 3x1 4x2 9 的解x 1,色，最大值z 35 5x 1 2x 2 8 2 2 (2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 max z 10x 1 5x 2 0x 3 0x 4 3x i 4x 2 X 3 9 st. 5x 1 2x 2 x 4 8 则P 3，P 4组成一个基。令x i X 2 得基可行解x 0,0,9,8，由此列出初始单纯形表 C j 10 5 0 0 c B 基 b X 1 X 2 X 3 X 4 0 x 3 9 3 4 1 0 0 x 4 8 [5] 2 0 1 C j Z j 10 5 C j 10 5 0 0 C B 基 b X 1 X 2 X 3 X 4 21 14 3 X 3 1 — 5 5 5 8 2 1 10 X 1 1 5 5 5 1 2 ° 8 9 min ,- 5 3

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学参考文献

运筹学教案(胡运权版)

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学(胡运权)第五版课后答案-运筹作业

运筹学基础及应用课后习题答案

运筹学(胡运权版)第三章运输问题课后习题答案

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学[胡运权]第五版课后答案,运筹作业

运筹学基础及应用

胡运权习题及答案(1)

第五版运筹学基础与应用-大题模拟试题及答案

胡运权习题及答案习题解答(6)

运筹学课后习题答案

运筹学(胡运权)第五版课后答案,运筹作业

运筹学胡运权 部分课后习题答案

运筹学基础及应用第四版胡运权主编课后练习答案

运筹学胡运权部分课后习题答案