第10章 一元回归及简单相关分析

第十章一元回归及简单相关分析
10.1对尿毒症患者采用低蛋白并补加基本氨基酸的食物进行治疗,分析该疗法对患者体内一些成分的影响。以下数据是在治疗前患者的基本数据[64]:
体重(BW)
/kg 体内总钾(TBK)
/mmol
血清尿素(UREA)
/(mmol·L-1)
73 3 147 19
70 3 647 36
72 3 266 25
53 2 650 25
97 3 738 34
77 3 982 36
63 2 900 49
54 3 194 38
66 3 930 16
53 3 419 34
70 3 978 34
63 2 747 26
65 4 181 46
88 3 678 41
82 3 540 39
69 3 912 19
91 4 138 35
62 2 896 43
74 3 410 50
90 3 679 23
74 3 855 38
71 2 750 50
59 3 583 31
80 3 268 47
66 2 846 45
115 4 804 65
111 5 290 38
64 2 960 45
71 3 610 24
69 2 905 31
计算三者之间的相关系数,并检验相关的显著性。
答:所用程序及计算结果如下:
options linesize=76 nodate;
data uremia;
infile 'e:\data\er10-1e.dat';
input bw tbk urea @@;
run;
proc corr nosimple;
var bw tbk urea;
run;
The SAS System
Correlation Analysis
3 'VAR' Variables: BW TBK UREA
Pearson Correlation Coefficients / Prob > |R| under Ho: Rho=0 / N = 30
BW TBK UREA
0.0 0.0001 0.1257
TBK 0.70594 1.00000 0.09661 0.0001 0.0 0.6116
UREA 0.28582 0.09661 1.00000 0.1257 0.6116 0.0
三个变量间,只有体重(BW)和体内总钾(TBK)间相关显著,r =0.705 94。相关系数的显著性概率P =0.000 1。
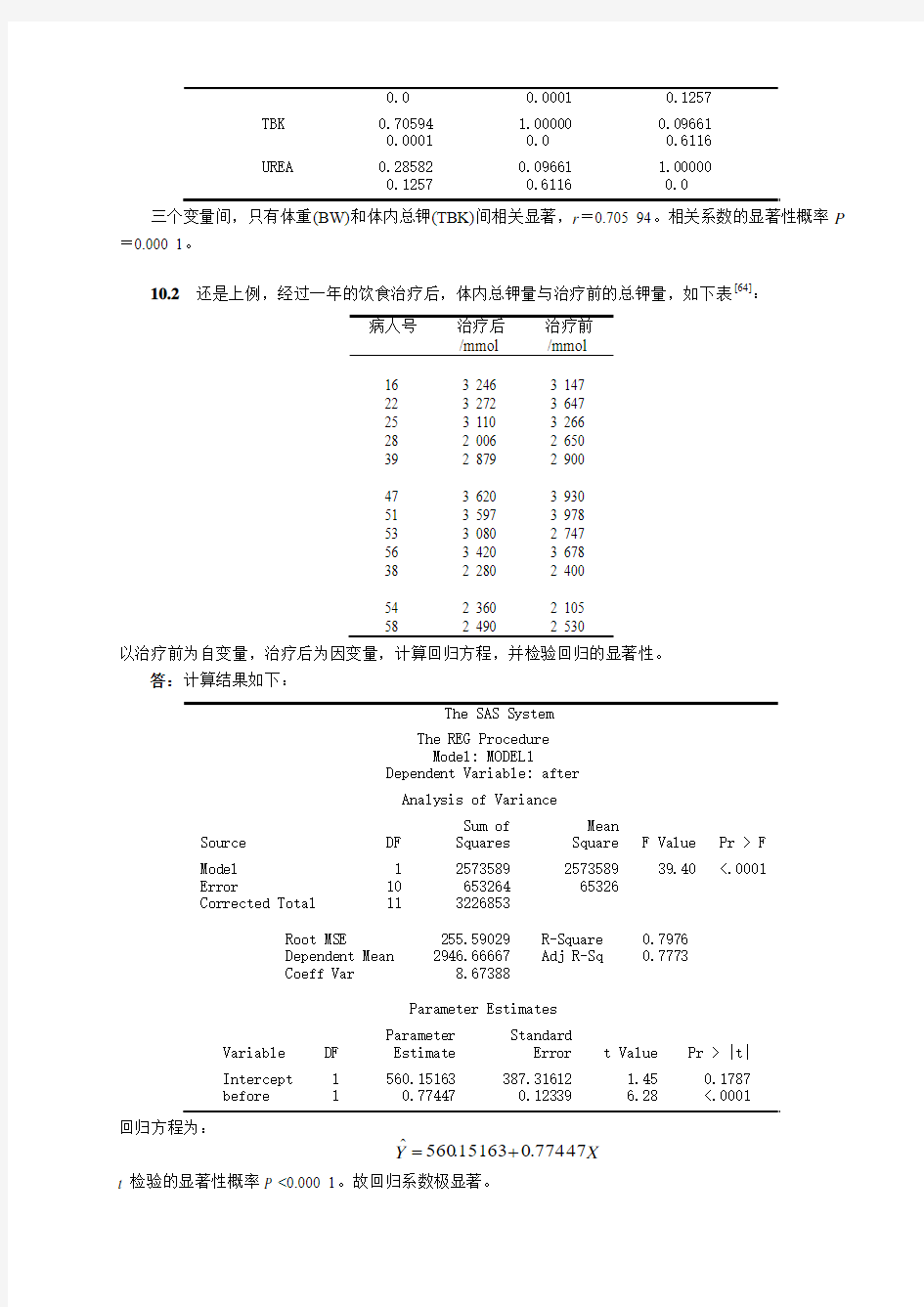
10.2 还是上例,经过一年的饮食治疗后,体内总钾量与治疗前的总钾量,如下表[64]:
病人号
治疗后 /mmol
治疗前 /mmol
16 3 246 3 147 22 3 272 3 647 25 3 110 3 266 28 2 006 2 650 39
2 879
2 900
47 3 620 3 930 51 3 597 3 978 53 3 080 2 747 56 3 420 3 678 38
2 280
2 400
54 2 360 2 105 58
2 490 2 530
以治疗前为自变量,治疗后为因变量,计算回归方程,并检验回归的显著性。
答:计算结果如下:
The SAS System
The REG Procedure Model: MODEL1
Dependent Variable: after
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 2573589 2573589 39.40 <.0001 Error 10 653264 65326 Corrected Total 11 3226853
Root MSE 255.59029 R-Square 0.7976 Dependent Mean 2946.66667 Adj R-Sq 0.7773 Coeff Var 8.67388
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 560.15163 387.31612 1.45 0.1787 before 1 0.77447 0.12339 6.28 <.0001
回归方程为:
X Y 47774.063151.560?+=
t 检验的显著性概率P <0.000 1。故回归系数极显著。
10.3调查河流中悬浮物每月沉淀的量与水流速度的关系,得到以下结果[65]:
流量
/(m3·min-1)每月上层沉积物
/t
流量
/(m3·min-1)
每月主流沉积物
/t
流量
/(m3·min-1)
每月下层沉积物
/t
1 651.3 425 468 1
2 181.6 1 990 300 2
3 640.1 2 010 730
848.6 209 455 9 902.3 1 626 786 11 269.9 671.326 832.6 183 412 3 592.4 488 599 3 405.2 148.755 621.4 147 799 3 325.3 471 549 1 398.6 39 156 598.6 108 025 1 763.8 112 404 1 144.6 24 843 574.3 200 537 1 429.7 89 201 1 126.4 32 939 228.4 50 386 1 404.4 79 615 675.4 9 913 204.8 57 608 1 337.6 84 191 285.6 1 189 188.1 30 947 1 128.6 62 034 174.0 264
16.3 1 826 823.1 87 925 104.2 881
655.9 52 395 97.4 259
595.1 66 379 47.1 367
569.1 29 913 45.9 70
273.9 20 497 41.3 136
265.8 22 469 32.6 70
236.7 22 704 3.4 13
236.2 27 566 1.2 4
145.8 7 463
142.7 11 281
97.2 9 257
70.0 3 699
63.7 3 955
32.8 2 636
27.2 1 232
18.0 1 068
17.0 584
15.6 400
10.2 456
7.9 195
6.6 114
以流量为自变量,月沉积物为因变量,计算回归方程。
答:首先对自变量和因变量做双对数变换,获得经对数变换后的回归方程,再通过反对数得到原始单位的回归方程。程序和结果如下:
options linesize=76 nodate;
data river;
infile 'E:\data\er10-3e.dat';
input upflow upsedim midflow midsedim lowflow lowsedim @@;
x1=log10(upflow); y1=log10(upsedim);
x2=log10(midflow); y2=log10(midsedim);
x3=log10(lowflow); y3=log10(lowsedim);
proc reg;
model y1=x1;
proc reg;
model y2=x2;
proc reg;
model y3=x3;
run;
(1)上层沉积物:
The SAS System
Model: MODEL1
Source DF Squares Square F Value Prob>F
Model 1 3.92128 3.92128 382.295 0.0001 Error 8 0.08206 0.01026 C Total 9 4.00334
Root MSE 0.10128 R-square 0.9795 Dep Mean 4.89337 Adj R-sq 0.9769 C.V. 2.06970
Parameter Estimates
Parameter Standard T for H0:
Variable DF Estimate Error Parameter=0 Prob > |T|
INTERCEP 1 1.890841 0.15686760 12.054 0.0001
X1 1 1.175010 0.06009554 19.552 0.0001
从参数估计列,得到如下回归方程:
变换为原单位后的方程为:
010175.11118775.77?X Y =
由t 检验的显著性概率可知,回归系数和常数项都是显著的。 (2)主流沉积物:
The SAS System
Model: MODEL1
Dependent Variable: Y2
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Prob>F
Model 1 35.58584 35.58584 1438.727 0.0001 Error 28 0.69256 0.02473 C Total 29 36.27840
Root MSE 0.15727 R-square 0.9809 Dep Mean 4.19618 Adj R-sq 0.9802 C.V. 3.74797
Parameter Estimates
Parameter Standard T for H0:
Variable DF Estimate Error Parameter=0 Prob > |T|
INTERCEP 1 1.366966 0.07992510 17.103 0.0001
X2 1 1.194288 0.03148616 37.931 0.0001
从参数估计列得到回归方程如下:
22288194.1966366.1?X Y '+='
变换为原单位后的方程为:
288194.122090279.23?X Y =
由t 检验的显著性概率可知,回归系数和常数项都是显著的。
(3)底层沉积物:
The SAS System
Model: MODEL1
11010175.1841890.1?X Y '+='
Source DF Squares Square F Value Prob>F
Model 1 20.99588 20.99588 26.414 0.0001 Error 15 11.92328 0.79489 C Total 16 32.91916
Root MSE 0.89156 R-square 0.6378 Dep Mean 2.92730 Adj R-sq 0.6137 C.V. 30.45683
Parameter Estimates
Parameter Standard T for H0:
Variable DF Estimate Error Parameter=0 Prob > |T|
INTERCEP 1 0.593156 0.50301446 1.179 0.2567 X3 1 0.996479 0.19388907 5.139 0.0001
从参数估计列得到回归方程如下:
33479996.0156593.0?X Y '+='
变换为原单位后的方程为:
479996.033826918.3?X Y =
由t 检验的显著性概率可知,回归系数是显著的。
10.4 一种治疗肺动脉高血压的药物treprostinil sodium ,研究给药剂量与血浆浓度之间的关系,当用静脉给药时得到以下结果[66](近似值):
剂 量 /(ng·kg -1·min -1
) 血浆药物浓度
/(pg·mL -1)
20
4 750 24 2 500 49 8 000 53
5 500 70
9 000
78 12 500 84 8 000 90 13 250 96 18 250 102
14 500
122 17 500 126
17 000
以剂量为自变量,血浆药物浓度为因变量,计算的回归方程,检验回归的显著性并绘出回归线。
答:计算结果如下:
The SAS System
Model: MODEL1
Dependent Variable: CONCEN
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Prob>F
Model 1 263507305.51 263507305.51 52.387 0.0001 Error 10 50299986.153 5029998.6153 C Total 11 313807291.67
Dep Mean 10895.83333 Adj R-sq 0.8237 C.V. 20.58370
Parameter Estimates
Parameter Standard T for H0:
Variable DF Estimate Error Parameter=0 Prob > |T|
INTERCEP 1 89.036517 1627.4120399 0.055 0.9574 DOSAGE 1 141.883547 19.60286907 7.238 0.0001
回归方程为:
X Y 547883.141517036.89?+=
从回归系数和常数项的显著性概率可知,回归系数是显著的,常数项是不显著的。散点图和回归线如下:
10.5 继续上题,这次是皮下给药,结果如下表[66](近似值):
剂 量 /(ng·kg -1·min -1
) 血浆药物浓度
/(pg·mL -1)
剂 量 /(ng·kg -1·min -1
) 血浆药物浓度 /(pg·mL -1)
50 7 500
12 1 000 52 7 750
13 1 750 64 14 250
15 2 500 17 3 750 66 10 250
28 6 250 67 13 000
67 10 000
29 3 250 67 5 750 30 2 500 70 10 000
32 5 250 36 4 250 73 8 750 38 6 250 75 10 000
80 16 250
38 7 000 80 10 250
38 6 750 80 8 500 44 3 500 44 9 750 87 11 000
47 5 000 95 15 250
49 5 750 100 11 250
50
6 000
问:(1)计算血浆药物浓度对剂量的回归方程,检验回归的显著性并绘出回归线。 (2)比较10.5和10.4两种给药方式的回归系数差异是否显著?
答:计算结果如下:
The SAS System
Model: MODEL1
Dependent Variable: CONCEN
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Prob>F
Model 1 401262581.37 401262581.37 84.935 0.0001 Error 32 151178595.1 4724331.0969 C Total 33 552441176.47
Root MSE 2173.55264 R-square 0.7263 Dep Mean 7823.52941 Adj R-sq 0.7178 C.V. 27.78225
Parameter Estimates
Parameter Standard T for H0:
Variable DF Estimate Error Parameter=0 Prob > |T|
INTERCEP 1 301.527681 897.27970517 0.336 0.7390 DOSAGE 1 139.905940 15.18070660 9.216 0.0001
回归方程为:
X Y 940905.139681527.301?+=
从回归系数和常数项的显著性概率可知,回归系数是显著的,常数项是不显著的。散点图和回归线如下:
比较两个回归系数:令10.4的回归系数为b 1,10.5的回归系数为b 2。统计假设为:
H 0:β1-β2=0 H A :β1-β2≠0
08
.060
706180.1507869602.19940905.139547883.1412
2
22212
1
=+-=
+-=
b b s
s b b t
显著性概率P =0.936 6,P >0.05,尚无足够理由拒绝H 0。结论:两个回归系数的差异不显著。
序号
4月份9月份
体重/g 体长/cm 体重/g 体长/cm
1 59.7 14.0 38.9 12.7
2 50.1 13.0 31.9 11.9
3 37.1 12.0 21.2 10.3
4 36.2 11.6 17.2 9.9
5 41.2 11.2 11.7 9.6
6 26.6 10.6 14.6 9.1
7 26.5 10.2 10.2 8.6
8 24.1 9.9 9.1 8.2
9 20.1 9.1 8.4 8.1
10 16.5 8.9 9.0 8.0
11 11.7 7.6 8.3 8.0
12 5.0 6.6 6.2 7.2
一般来说,鱼的体重(Y)在体长(X)上的回归符合以下关系:Y = aX b。计算回归方程,绘出对数尺度下的回归线,检验回归的显著性,并比较4月份和9月份两个回归系数的差异是否显著。
答:记4月份的样本为样本1,9月份的样本为样本2。程序和结果如下:
options linesize=76 nodate;
data river;
infile 'E:\data\er10-6e.dat';
input fw fl nw nl @@;
y1=log10(fw); x1=log10(fl);
y2=log10(nw); x2=log10(nl);
proc reg;
model y1=x1;
model y2=x2;
symbol v=star i=rl l=1 w=2 c=black;
proc gplot;
plot y1*x1;
plot y2*x2;
run;
(1)4月份的回归分析和回归线:
The SAS System
The REG Procedure
Model: MODEL1
Dependent Variable: y1
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 0.94059 0.94059 260.55 <.0001
Error 10 0.03610 0.00361
Corrected Total 11 0.97669
Root MSE 0.06008 R-Square 0.9630
Dependent Mean 1.39473 Adj R-Sq 0.9593
Coeff Var 4.30790
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -1.72319 0.19394 -8.89 <.0001
x1 1 3.09439 0.19170 16.14 <.0001
X Y 39094.319723.1?+-=
从t 的显著性概率可以得知,常数项和回归系数都是显著的。
(2)9月份的回归分析和回归线:
The SAS System
The REG Procedure Model: MODEL1
Dependent Variable: y2
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 0.65994 0.65994 320.79 <.0001 Error 10 0.02057 0.00206 Corrected Total 11 0.68051
Root MSE 0.04536 R-Square 0.9698 Dependent Mean 1.12048 Adj R-Sq 0.9667 Coeff Var 4.04795
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -2.04592 0.17727 -11.54 <.0001 x2 1 3.28993 0.18368 17.91 <.0001
对数尺度下的回归方程和回归线为:
X Y 93289.392045.2?+-=
从t 的显著性概率可以得知,常数项和回归系数都是显著的。
(3)回归系数的比较:
统计假设为:
H 0:β1-β2=0 H A :β1-β2≠0
5
736.068
183.070191.093289.339094.32
2
22212
1
=+-=
+-=
b b s
s b b t
显著性概率P =0.47,P >0.05,尚无足够理由拒绝H 0。结论:两个回归系数的差异不显著。
10.7 新疆维吾尔族和哈萨克族男生各100名,他们的立定跳远平均成绩与年龄之间的关系如下表所示[10]:
年龄/a 7
8 9 10 11 12 维吾尔族/cm 124.51 132.65 138.59 143.39 151.74 160.91 哈萨克族/cm 135.80
146.52 153.34 162.88 171.10 174.29 年龄/a 13 14 15 16 17 18 维吾尔族/cm 169.31 184.22 195.57 200.51 207.84 217.24 哈萨克族/cm 185.88
190.24 211.21 228.63 235.07 233.65
分别计算两个民族的成绩与年龄之间的相关系数,并检验两个相关系数的显著性。
答:程序和结果如下:
options linesize=76 nodate; data jump;
infile 'e:\data\er10-7e.dat'; input age wei ha @@; run;
proc corr nosimple; var age wei ha; run;
The SAS System
The CORR Procedure
3 Variables: age wei ha
Pearson Correlation Coefficients, N = 12
Prob > |r| under H0: Rho=0
age wei ha
age 1.00000 0.99494 0.98708 <.0001 <.0001
wei 0.99494 1.00000 0.98651 <.0001 <.0001
ha 0.98708 0.98651 1.00000
<.0001 <.0001
维吾尔族男生年龄与成绩间的相关系数 r 维=0.994 94;哈萨克族男生年龄与成绩间的相关系数 r 哈=0.987 08。这两个相关系数都是极显著的。
10.8 心脏的冠状窦口直径(d )与冠状窦瓣宽(w )和窦瓣高(h )存在一定关联,下面测量了从新生儿到儿童末期的6个年龄组的窦口直径、窦瓣宽和窦瓣高,结果见下表[68]:
ⅠⅡⅢⅣⅤⅥ
窦口直径/mm 3.19 4.43 4.96 5.81 6.30 7.98
窦瓣宽/mm 4.64 6.42 7.32 7.68 8.99 10.30
窦瓣高/mm 1.68 3.93 4.08 4.41 4.94 5.02
分别计算窦瓣宽和窦瓣高与窦口直径间的相关系数,并检验相关系数的显著性。
答:所用程序与第7题一样,这里仅给出结果。
The SAS System
The CORR Procedure
3 Variables: diameter width height
Pearson Correlation Coefficients, N = 6
Prob > |r| under H0: Rho=0
diameter width height
diameter 1.00000 0.98660 0.87117
0.0003 0.0238
width 0.98660 1.00000 0.91358
0.0003 0.0109
height 0.87117 0.91358 1.00000
0.0238 0.0109
从程序运行的结果可以得出:r d-w=0.986 60,P=0.000 3,相关极显著;r d-h=0.871 17,P=0.023 8,相关显著。
10.9Cu2+和Zn2+对尾草履虫的急性毒性试验结果如下[69]:
Cu2+Zn2+
浓度/( mg ·L-1) 死亡率/% 浓度/( mg ·L-1) 死亡率/%
0 2.5 0 4.2
0.14 5.1 1.8 5.2
0.18 15.4 3.2 21.7
0.24 40.2 5.6 33.0
0.32 50.4 10.0 46.1
0.42 63.0 18.0 62.6
0.56 79.5 32.0 73.0
0.75 93.2 56.0 89.6
分别计算Cu2+和Zn2+对尾草履虫的半致死剂量。
答:利用SAS软件包中正态分布的分位数函数,对死亡率做概率变换,对浓度做常用对数变换。以正态尺度的死亡率为自变量,以对数尺度的浓度为因变量,计算回归方程。程序和结果如下:options linesize=76 nodate;
data parameci;
infile 'e:\data\er10-9e.dat';
input cuconcen cudearat znconcen zndearat @@;
xcu=probit(cudearat/100);
ycu=log10(cuconcen);
xzn=probit(zndearat/100);
yzn=log10(znconcen);
run;
proc reg;
model ycu=xcu;
model yzn=xzn;
run;
The SAS System
The REG Procedure Model: MODEL1
Dependent Variable: ycu
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 0.40835 0.40835 241.67 <.0001 Error 5 0.00845 0.00169 Corrected Total 6 0.41679
Root MSE 0.04111 R-Square 0.9797 Dependent Mean -0.49525 Adj R-Sq 0.9757 Coeff Var -8.30000
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -0.48662 0.01555 -31.30 <.0001
xcu 1 0.24545 0.01579 15.55 <.0001
当死亡率为50%时,
12326.0?62486.0?lg =-=Y
Y
故Cu 2+
对草履虫的半致死剂量为0.326 12 mg/L 。 (2)Zn 2+:
The SAS System
The REG Procedure Model: MODEL2
Dependent Variable: yzn
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 1.70301 1.70301 213.00 <.0001 Error 5 0.03998 0.00800 Corrected Total 6 1.74299
Root MSE 0.08942 R-Square 0.9771 Dependent Mean 1.00246 Adj R-Sq 0.9725 Coeff Var 8.91979
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 1.06262 0.03405 31.21 <.0001 xzn 1 0.55944 0.03833 14.59 <.0001
当死亡率为50%时,
01551.11?62062.1?lg ==Y
Y
故Zn 2+
对草履虫的半致死剂量为11.551 01 mg/L 。
与相变点温度(因变量)存在以下关系[70]:
序号3
(自变量)(因变量)
1 1.00 54.1
2 1.50 48.0
3 1.81 46.6
4 2.50 41.1
5 2.91 39.1
6 3.8
7 35.5
7 5.00 32.9
8 5.80 29.6
9 7.50 26.8
10 8.39 25.1
11 10.00 22.4
做出散点图,并求出回归方程。
答:程序不再给出,这里只给出结果。散点图和回归线如下:
回归分析见下表:
The SAS System
The REG Procedure
Model: MODEL1
Dependent Variable: temp
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 966.81811 966.81811 97.17 <.0001
Error 9 89.54371 9.94930
Corrected Total 10 1056.36182
Root MSE 3.15425 R-Square 0.9152
Dependent Mean 36.47273 Adj R-Sq 0.9058
Coeff Var 8.64825
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 51.31644 1.78099 28.81 <.0001
rate 1 -3.24743 0.32943 -9.86 <.0001
X Y 43247.344316.51?-=
回归系数的t 检验和回归模型的方差分析都指出,回归是极显著的。
10.11 4到10月龄胎儿的肝重与肝的Ca 含量存在以下关系[71]:
肝 重/g
6.48 13.02 24.17 44.86 58.39 75.58 86.47 Ca 含量/(μg ·g -1
干重) 1 271.0 1440.9 1016.6 663.7 516.3 535.9 492.5
求钙含量在肝重上的回归方程并检验回归的显著性。
答:结果如下:
options linesize=76 nodate; data fetus;
input liver calcium @@; cards;
6.48 1271.0 13.02 1440.9 24.17 1016.6 44.86 663.7 58.39 516.3 75.58 535.9 86.47 492.5 ;
proc reg ;
model calcium=liver; run;
The SAS System
The REG Procedure Model: MODEL1
Dependent Variable: calcium
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 788984 788984 28.65 0.0031 Error 5 137679 27536 Corrected Total 6 926663
Root MSE 165.93934 R-Square 0.8514 Dependent Mean 848.12857 Adj R-Sq 0.8217 Coeff Var 19.56535
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 1364.29113 115.03041 11.86 <.0001 liver 1 -11.69414 2.18466 -5.35 0.0031
由此得出回归方程:
X Y 14694.1113291.3641?-=
对回归模型的方差分析和回归系数的t 检验都指出,回归是极显著的。
10.12 青菜对14CO 2的富集系数(CF 值)如下[72]:
时间/d 菜 心 叶 子 6 24.6 13.8 12 53.4 30.9 18 82.0 41.9 24 100.1 63.2 36 114.1 96.8 48
156.4 135.6
答:程序不再给出,这里只给出结果。 (1)菜心:
The SAS System
The REG Procedure Model: MODEL1
Dependent Variable: cfheart
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 10280 10280 86.05 0.0008 Error 4 477.84863 119.46216 Corrected Total 5 10758
Root MSE 10.92987 R-Square 0.9556 Dependent Mean 88.43333 Adj R-Sq 0.9445 Coeff Var 12.35945
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 18.88039 8.72513 2.16 0.0965
time 1 2.89804 0.31241 9.28 0.0008
由上表得出回归方程: X Y 04898.239880.18?+=
回归系数b 1是极显著的。 (2)叶子:
The SAS System
The REG Procedure Model: MODEL2
Dependent Variable: cfleaf
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 10269 10269 1108.25 <.0001 Error 4 37.06559 9.26640 Corrected Total 5 10307
Root MSE 3.04408 R-Square 0.9964 Dependent Mean 63.70000 Adj R-Sq 0.9955 Coeff Var 4.77877
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -5.81765 2.43003 -2.39 0.0748
time 1 2.89657 0.08701 33.29 <.0001
由上表得出回归方程: X Y 57896.265817.5?+-=
回归系数b 2是极显著的。
(3)回归系数的比较:
统计假设为:
H 0:β1-β2=0 H A :β1-β2≠0
53
004.001
087.041312.057896.204898.22
2
22212
1
=+-=
+-=
b b s
s b b t
显著性概率P =0.9965,P >0.05,尚无足够理由拒绝H 0。结论:两个回归系数的差异不显著。
10.13 人工测定蚊密度与气温存在以下关系[73]:
序号 蚊密度*
气 温 /℃ 序号 蚊密度* 气 温 /℃ 序号 蚊密度* 气 温
/℃
1
52.8 23.0 11 134.3 25.3 21 193.7 27.9 2 104.4 23.5 12 162.7 27.2 22 165.1 27.4 3 74.7 21.9 13 341.4 28.3 23 74.9 28.7 4 79.6 23.7 14 292.4 29.3 24 102.1 26.8 5 43.8 22.5
15 265.2 27.8
25 185.0 24.4
6 47.5 21.0 16 230.6 28.3 26 175.8 25.0
7 191.5 24.9 17 259.
8 30.1 27 203.5 26.3 8 157.8 25.6 18 148.5 29.4 28 138.5 23.3
9 204.3 26.0 19 331.4 30.2 29 93.1 26.6 10
232.8
25.5
20
326.3
27.5
30
97.0
24.8
以气温作为自变量,蚊密度作为因变量,求回归方程并对回归方程做方差分析。
答:结果如下:
The SAS System
The REG Procedure Model: MODEL1
Dependent Variable: density
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 103565 103565 25.51 <.0001 Error 28 113674 4059.77886 Corrected Total 29 217239
Root MSE 63.71639 R-Square 0.4767 Dependent Mean 170.35000 Adj R-Sq 0.4580 Coeff Var 37.40323
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -459.98640 125.34184 -3.67 0.0010 temp 1 24.17552 4.78653 5.05 <.0001
由以上结果得到回归方程: X Y 52175.2440986.459?+-=
方差分析表:
变差来源 平方和 自由度 均方 F
P
剩余113 674 28 4 059.778 86
总和217 239 29
10.14马鹿下臼齿咀嚼面宽度与年龄之间存在以下关系[48]:
序号年龄
/a
下臼齿咀嚼面宽度/mm
1 2.
5
8.65 8.90 8.30 8.80
2 3.
5 9.60 8.30 7.80 8.40 8.70 9.40 7.50 7.90 8.90 8.35 8.40
3 4.
5 10.13 8.65 10.00 10.90 9.92 10.00 10.14 10.12 10.15 9.10 10.17 9.80 9.72 9.82 10.00 10.15 8.80
4 5.
5 10.75 11.68 10.30 10.22 10.00 11.90 11.85 11.90 11.85 10.68
5 6.
5 11.30 12.70 11.48 11.87 10.20 10.82 11.52 11.60 10.25 11.00 11.30
6 7.
5
10.40 11.00 12.50 13.50 9.98
7 8.
5
12.16 12.80 11.88 11.10 11.48 11.40 12.10 10.15
8 9.
5
12.72 11.68 12.80 11.35 13.33
9 13.
5
12.20
10 17.
5
14.03
以年龄为自变量,咀嚼面宽度为因变量,计算回归方程。这是一个有重复数据的回归问题,它的计算与无重复时相似,只是DATA步略有不同。
答:程序如下:
options linesize=76 nodate;
data deer;
infile 'E:\data\er10-14e.dat';
do i=1 to 10;
input n age @@;
do j=1 to n;
input width @@;
output;
end;
end;
proc reg;
model width=age;
run;
The SAS System
The REG Procedure
Model: MODEL1
Dependent Variable: width
Analysis of Variance
Source DF Squares Square F Value Pr > F
Model 1 98.09381 98.09381 113.00 <.0001 Error 71 61.63552 0.86811 Corrected Total 72 159.72934
Root MSE 0.93172 R-Square 0.6141 Dependent Mean 10.53699 Adj R-Sq 0.6087 Coeff Var 8.84240
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 7.81780 0.27808 28.11 <.0001 age 1 0.45580 0.04288 10.63 <.0001
由以上数据得到回归方程:
X Y 80455.080817.7?+=
经t 检验回归系数和常数项都是显著的。
10.15 端粒(telomere )的长度随着年龄的增长而逐渐缩短,因此有可能根据端粒的大小推断出个体的年龄。采用末端限制片段(terminal restriction fragment, TRF )长度来确定不同年龄组端粒的大小。年龄组(岁)和各年龄组外周血白细胞TRF 平均长度(kb )的测定结果见下表[74]:
1 2.0
14.29 2 9.0 12.92 3 19.0 12.16 4 29.0 11.91 5 39.0
11.68
6 49.0 11.25
7 59.0 10.94
8 69.0 10.3
9 9
77.5
10.31
以TRF 为自变量,年龄为因变量,求出最佳拟合回归方程。
答:求最佳拟合方程,可以通过绘图法,也可以通过比较剩余均方来确定。绘图法比较直观,在这里我们采用绘图法。
(1)不变换:
(2)log 10(age)变换:
(3)sqrt(age)变换:
比较以上三个图形,显然对年龄做平方根变换后,直线化的效果最好,则方差分析表为:
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 28.65083 1.42367 20.12 <.0001 trf 1 -1.94297 0.12043 -16.13 <.0001
变换后的回归方程为: X Y 97942.183650.28?-='
10.16 用18种不同水体配制成培养基,培养基中的磷(P )浓度及用该培养基培养的玫瑰拟衣藻
(Chloromonas rosae )的生长速率见下表[75]:
水体号 P 浓度/(mg ·L -1) 生长速率/(μ)
1
0.101 0 0.244 0 2 0.082 0 0.198 9 3 0.061 0 0.238 2 4 0.028 0 0.246 0 5 0.030 0
0.171 6
6 0.032 0 0.216 3
7 0.210 0 0.413
8 8 0.150 0 0.332 8
9 0.160 0 0.268 4 10
0.016 8 0.094 8
11 0.012 0 0.099 3 12 0.012 8 0.165 0
14 0.006 0 0.006 7
15 0.006 4 0.059 2
16 0.004 2 0.033 3
17 0.003 0 0.019 8
18 0.003 2 - 0.014 7
以P浓度为自变量,生长速率为因变量,在直角坐标系中画出散点图,求出回归方程,并检验回归的显著性。
答:对自变量(P浓度)做自然对数变换,用变换后的数据进行分析。程序和结果如下:options linesize=76 nodate;
data leaves;
infile 'e:\data\er10-16e.dat';
input p rate @@;
x=log(p); y=rate;
run;
proc gplot;
plot y*x;
proc reg ;
model y=x;
run;
The SAS System
The REG Procedure
Model: MODEL1
Dependent Variable: y
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 0.21685 0.21685 128.01 <.0001
Error 16 0.02710 0.00169
Corrected Total 17 0.24395
Root MSE 0.04116 R-Square 0.8889
Dependent Mean 0.16027 Adj R-Sq 0.8820
Coeff Var 25.67984
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 0.46581 0.02869 16.23 <.0001
x 1 0.08059 0.00712 11.31 <.0001
(1)用Excel作一元线性回归分析
实验四(1)用Excel作一元线性回归分析 实验名称:回归分析 实验目的:学会应用软件实验一元线性回归,多元线性回归和非线性回归模型的求解及应用模型解决相应地理问题。 1 利用Excel进行一元线性回归分析 第一步,录入数据 以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。录入结果见下图(图1)。 图1 第二步,作散点图 如图2所示,选中数据(包括自变量和因变量),点击“图表向导”图标;或者在 “插入”菜单中打开“图表(H)”。图表向导的图标为。选中数据后,数据变为蓝色(图2)(office2003)。插入-图表(office2007)
图2 点击“图表向导”以后,弹出如下对话框(图3): 图3 在左边一栏中选中“XY散点图”,点击“完成”按钮,立即出现散点图的原始形式(图4):
图4 第三步,回归 观察散点图,判断点列分布是否具有线性趋势。只有当数据具有线性分布特征时,才能采用线性回归分析方法。从图中可以看出,本例数据具有线性分布趋势,可以进行线性回归。回归的步骤如下: ⑴ 首先,打开“工具”下拉菜单,可见数 据分析选项(见图5) (office2003)。数据-数据分析(office2007) : 图5 用鼠标双击“数据分析”选项,弹出“数据分析”对话框(图6):
图6 ⑵然后,选择“回归”,确定,弹出如下选项表(图7): 图7 进行如下选择:X、Y值的输入区域(B1:B11,C1:C11),标志,置信度(95%),新工作表组,残差,线性拟合图(图8-1)。 或者:X、Y值的输入区域(B2:B11,C2:C11),置信度(95%),新工作表组,残差,线性拟合图(图8-2)。 注意:选中数据“标志”和不选“标志”,X、Y值的输入区域是不一样的:前者包括数据标志: 最大积雪深度x(米)灌溉面积y(千亩) 后者不包括。这一点务请注意(图8)。
一元线性回归分析实验报告
一元线性回归在公司加班 制度中的应用 院(系): 专业班级: 学号姓名: 指导老师: 成 绩: 完成时间 :
一元线性回归在公司加班制度中的应用 一、实验目的 掌握一元线性回归分析的基本思想与操作,可以读懂分析结果,并写出回归方程,对回归方程进行方差分析、显著性检验等的各种统计检验 二、实验环境 SPSS21、0 windows10、0 三、实验题目 一家保险公司十分关心其总公司营业部加班的程度,决定认真调查一下现状。经10周时间,收集了每周加班数据与签发的新保单数目,x 为每周签发的新保单数目,y 为每周加班时间(小时),数据如表所示 y 3、5 1、0 4、0 2、0 1、0 3、0 4、5 1、5 3、0 5、0 1. 画散点图。 2. x 与y 之间大致呈线性关系? 3. 用最小二乘法估计求出回归方程。 4. 求出回归标准误差σ∧ 。 5. 给出0 β∧ 与1 β∧ 的置信度95%的区间估计。 6. 计算x 与y 的决定系数。 7. 对回归方程作方差分析。 8. 作回归系数1 β∧ 的显著性检验。 9. 作回归系数的显著性检验。 10. 对回归方程做残差图并作相应的分析。 11. 该公司预测下一周签发新保单01000x =张,需要的加班时间就是多少?
12.给出0y的置信度为95%的精确预测区间。 13.给出 () E y的置信度为95%的区间估计。 四、实验过程及分析 1、画散点图 如图就是以每周加班时间为纵坐标,每周签发的新保单为横坐标绘制的散点图,从图中可以瞧出,数据均匀分布在对角线的两侧,说明x与y之间线性关系良好。 2、最小二乘估计求回归方程 系数a 模型非标准化系数标准系数t Sig、 B 的 95、0% 置信区间 B 标准误差试用版下限上限
案例分析(一元线性回归模型)
案例分析报告(2014——2015学年第一学期) 课程名称:预测与决策 专业班级:电子商务1202 学号:2204120202 学生姓名:陈维维 2014 年11月
案例分析(一元线性回归模型) 我国城镇居民家庭人均消费支出预测 一、研究目的与要求 居民消费在社会经济的持续发展中有着重要的作用,居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长,而且这也是人民生活水平的具体体现。从理论角度讲,消费需求的具体内容主要体现在消费结构上,要增加居民消费,就要从研究居民消费结构入手,只有了解居民消费结构变化的趋势和规律,掌握消费需求的热点和发展方向,才能为消费者提供良好的政策环境,引导消费者合理扩大消费,才能促进产业结构调整与消费结构优化升级相协调,才能推动国民经济平稳、健康发展。例如,2008年全国城镇居民家庭平均每人每年消费支出为11242.85元,最低的青海省仅为人均8192.56元,最高的上海市达人均19397.89元,上海是黑龙江的2.37倍。为了研究全国居民消费水平及其变动的原因,需要作具体的分析。影响各地区居民消费支出有明显差异的因素可能很多,例如,零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。为了分析什么是影响各地区居民消费支出有明显差异的最主要因素,并分析影响因素与消费水平的数量关系,可以建立相应的计量经济模型去研究。 二、模型设定 我研究的对象是各地区居民消费的差异。居民消费可分为城镇居民消费和农村居民消费,由于各地区的城镇与农村人口比例及经济结构有较大差异,最具有直接对比可比性的是城市居民消费。而且,由于各地区人口和经济总量不同,只能用“城镇居民每人每年的平均消费支出”来比较,而这正是可从统计年鉴中获得数据的变量。 所以模型的被解释变量Y选定为“城镇居民每人每年的平均消费支出”。 因为研究的目的是各地区城镇居民消费的差异,并不是城镇居民消费在不同时间的变动,所以应选择同一时期各地区城镇居民的消费支出来建立模型。因此建立的是2008年截面数据模型。影响各地区城镇居民人均消费支
一元线性回归分析的结果解释
一元线性回归分析的结果解释 1.基本描述性统计量 分析:上表是描述性统计量的结果,显示了变量y和x的均数(Mean)、标准差(Std. Deviation)和例数(N)。 2.相关系数 分析:上表是相关系数的结果。从表中可以看出,Pearson相关系数为0.749,单尾显著性检验的概率p值为0.003,小于0.05,所以体重和肺活量之间具有较强的相关性。 3.引入或剔除变量表
分析:上表显示回归分析的方法以及变量被剔除或引入的信息。表中显示回归方法是用强迫引入法引入变量x的。对于一元线性回归问题,由于只有一个自变量,所以此表意义不大。 4.模型摘要 分析:上表是模型摘要。表中显示两变量的相关系数(R)为0.749,判定系数(R Square)为0.562,调整判定系数(Adjusted R Square)为0.518,估计值的标准误差(Std. Error of the Estimate)为0.28775。 5.方差分析表 分析:上表是回归分析的方差分析表(ANOVA)。从表中可以看出,回归的均方(Regression Mean Square)为1.061,剩余的均方(Residual Mean Square)为0.083,F检验统计量的观察值为12.817,相应的概率p 值为0.005,小于0.05,可以认为变量x和y之间存在线性关系。
6.回归系数 分析:上表给出线性回归方程中的参数(Coefficients)和常数项(Constant)的估计值,其中常数项系数为0(注:若精确到小数点后6位,那么应该是0.000413),回归系数为0.059,线性回归参数的标准误差(Std. Error)为0.016,标准化回归系数(Beta)为0.749,回归系数T检验的t统计量观察值为3.580,T检验的概率p值为0.005,小于0.05,所以可以认为回归系数有显著意义。由此可得线性回归方程为: y=0.000413+0.059x 7.回归诊断 分析:上表是对全部观察单位进行回归诊断(Casewise Diagnostics-all cases)的结果显示。从表中可以看出每一例的标准
简单线性相关(一元线性回归分析)..
第十三讲 简单线性相关(一元线性回归分析) 对于两个或更多变量之间的关系,相关分析考虑的只是变量之间是否相关、相关的程度,而回归分析关心的问题是:变量之间的因果关系如何。回归分析是处理一个或多个自变量与因变量间线性因果关系的统计方法。如婚姻状况与子女生育数量,相关分析可以求出两者的相关强度以及是否具有统计学意义,但不对谁决定谁作出预设,即可以相互解释,回归分析则必须预先假定谁是因谁是果,谁明确谁为因与谁为果的前提下展开进一步的分析。 一、一元线性回归模型及其对变量的要求 (一)一元线性回归模型 1、一元线性回归模型示例 两个变量之间的真实关系一般可以用以下方程来表示: Y=A + BX + ε 方程中的A 、B 是待定的常数,称为模型系数,ε是残差,是以X 预测Y 产生的误差。 两个变量之间拟合的直线是: y a bx ∧ =+ y ∧ 是 y 的拟合值或预测值,它是在X 条件下Y 条件均值的估计 a 、 b 是回归直线的系数,是总体真实直线A 、B 的估计值,a 即 constant 是截距,当自变量的值为0时,因变量的值。 b 称为回归系数,指在其他所有的因素不变时,每一单位自变量的变化引起的因变量的变化。 可以对回归方程进行标准化,得到标准回归方程: y x ∧ =β β 为标准回归系数,表示其他变量不变时,自变量变化一个标准差单位(Z X X S j j j = -),因变量Y 的标准差的平均变化。
由于标准化消除了原来自变量不同的测量单位,标准回归系数之间是可以比较的,绝对值的大小代表了对因变量作用的大小,反映自变量对Y的重要性。 (二)对变量的要求:回归分析的假定条件 回归分析对变量的要求是: 自变量可以是随机变量,也可以是非随机变量。自变量X值的测量可以认为是没有误差的,或者说误差可以忽略不计。 回归分析对于因变量有较多的要求,这些要求与其它的因素一起,构成了回归分析的基本条件:独立、线性、正态、等方差。 (三)数据要求 模型中要求一个因变量,一个或多个自变量(一元时为1个自变量)。 因变量:要求间距测度,即定距变量。 自变量:间距测度(或虚拟变量)。 二、在对话框中做一元线性回归模型 例1:试用一元线性回归模型,分析大专及以上人口占6岁及以上人口的比例(edudazh)与人均国内生产总值(agdp)之间的关系。 本例使用的数据为st2004.sav,操作步骤及其解释如下: (一)对两个变量进行描述性分析 在进行回归分析以前,一个比较好的习惯是看一下两个变量的均值、标准差、最大值、最小值和正态分布情况,观察数据的质量、缺少值和异常值等,缺少值和异常值经常对线性回归分析产生重要影响。最简单的,我们可以先做出散点图,观察变量之间的趋势及其特征。通过散点图,考察是否存在线性关系,如果不是,看是否通过变量处理使得能够进行回归分析。如果进行了变量转换,那么应当重新绘制散点图,以确保在变量转换以后,线性趋势依然存在。 打开st2004.sav数据→单击Graphs → S catter →打开Scatterplot 对话框→单击Simple →单击 Define →打开 Simple Scatterplot对话框→点选 agdp到 Y Axis框→点选 edudazh到 X Aaxis框内→单击 OK 按钮→在SPSS的Output窗口输出所需图形。 图12-1 大专及以上人口占6岁及以上人口比例与人均国内生产总值的散点图
用Excel做线性回归分析报告
用Excel进行一元线性回归分析 Excel功能强大,利用它的分析工具和函数,可以进行各种试验数据的多元线性回归分析。本文就从最简单的一元线性回归入手. 在数据分析中,对于成对成组数据的拟合是经常遇到的,涉及到的任务有线性描述,趋势预测和残差分析等等。很多专业读者遇见此类问题时往往寻求专业软件,比如在化工中经常用到的Origin和数学中常见的MATLAB等等。它们虽很专业,但其实使用Excel就完全够用了。我们已经知道在Excel自带的数据库中已有线性拟合工具,但是它还稍显单薄,今天我们来尝试使用较为专业的拟合工具来对此类数据进行处理。 文章使用的是2000版的软件,我在其中的一些步骤也添加了2007版的注解. 1 利用Excel2000进行一元线性回归分析 首先录入数据. 以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。录入结果见下图(图1)。 图1 第二步,作散点图 如图2所示,选中数据(包括自变量和因变量),点击“图表向导”图标;或者在“插入”菜单中打开“图表(H)(excel2007)”。图表向导的图标为。选中数据后,数据变为蓝色(图2)。
图2 点击“图表向导”以后,弹出如下对话框(图3): 图3 在左边一栏中选中“XY散点图”,点击“完成”按钮,立即出现散点图的原始形式(图4):
灌溉面积y(千亩) 01020304050600 10 20 30 灌溉面积y(千亩) 图4 第三步,回归 观察散点图,判断点列分布是否具有线性趋势。只有当数据具有线性分布特征时,才能采用线性回归分析方法。从图中可以看出,本例数据具有线性分布趋势,可以进行线性回归。回归的步骤如下: ⑴ 首先,打开“工具”下拉菜单,可见数据分析选项(见图5)(2007为”数据”右端的”数据分析”): 图5 用鼠标双击“数据分析”选项,弹出“数据分析”对话框(图6):
一元线性回归,方差分析,显著性分析
一元线性回归分析及方差分析与显著性检验 某位移传感器的位移x 与输出电压y 的一组观测值如下:(单位略) 设x 无误差,求y 对x 的线性关系式,并进行方差分析与显著性检验。 (附:F 0。10(1,4)=4.54,F 0。05(1,4)=7.71,F 0。01(1,4)=21.2) 回归分析是研究变量之间相关关系的一种统计推断法。 一. 一元线性回归的数学模型 在一元线性回归中,有两个变量,其中 x 是可观测、可控制的普通变量,常称它为自变量或控制变量,y 为随机变量,常称其为因变量或响应变量。通过散点图或计算相关系数判定y 与x 之间存在着显著的线性相关关系,即y 与x 之间存在如下关系: y =a +b ?x +ε (1) 通常认为ε~N (0,δ2)且假设δ2与x 无关。将观测数据(x i ,y i ) (i=1,……,n)代入(1)再注意样本为简单随机样本得: {y i =a +b ?x i +εi ε1?εn 独立同分布N (0,σ2) (2) 称(1)或(2)(又称为数据结构式)所确定的模型为一元(正态)线性回归模型。 对其进行统计分析称为一元线性回归分析。 模型(2)中 EY= a +b ?x ,若记 y=E(Y),则 y=a+bx,就是所谓的一元线性回归方程,其图象就是回归直线,b 为回归系数,a 称为回归常数,有时也通称 a 、b 为回归系数。 设得到的回归方程 bx b y +=0? 残差方程为N t bx b y y y v t t t i ,,2,1,?0Λ=--=-= 根据最小二乘原理可求得回归系数b 0和b 。 对照第五章最小二乘法的矩阵形式,令 ?????? ? ??=??? ? ??=??? ???? ??=??????? ??=N N N v v v V b b b x x x X y y y Y M M M M 2102121?111 则误差方程的矩阵形式为 V b X Y =-? 对照X A L V ?-=,设测得值 t y 的精度相等,则有
一元线性回归分析教程文件
一元线性回归分析论 文
一元线性回归分析的应用 ——以微生物生长与温度关系为例 摘要:一元线性回归预测法是分析一个因变量与一个自变量之间的线性关系的预测方法。应用最小二乘法确定直线,进而运用直线进行预测。本文运用一元线性回归分析的方法,构建模型并求出模型参数,对分析结果的显著性进行了假设检验,从而了微生物生长与温度间的关系。 关键词:一元线性回归分析;最小二乘法;假设检验;微生物;温度 回归分析是研究变量之间相关关系的统计学方法,它描述的是变量间不完全确定的关系。回归分析通过建立模型来研究变量间的这种关系,既可以用于分析和解释变量间的关系,又可用于预测和控制,进而广泛应用于自然科学、工程技术、经济管理等领域。本文尝试用一元线性回归分析方法为微生物生长与温度之间的关系建模,并对之后几年的情况进行分析和预测。 1 一元线性回归分析法原理 1.1 问题及其数学模型 一元线性回归分析主要应用于两个变量之间线性关系的研究,回归模型模型为εββ++=x Y 10,其中10,ββ为待定系数。实际问题中,通过观测得到n 组数据(X i ,Y i )(i=1,2,…,n ),它们满足模型i i i x y εββ++=10(i=1,2,…,n )并且通常假定E(εi )=0,V ar (εi )=σ2各εi 相互独立且服从正态分布。回归分析就是根据样 本观察值寻求10,ββ的估计10?,?ββ,对于给定x 值, 取x Y 10?? ?ββ+=,作为x Y E 10)(ββ+=的估计,利用最小二乘法得到10,ββ的估计10?,?ββ,其中 ??? ? ??????? ??-???? ??-=-=∑ ∑ ==n i i n i i i x n x xy n y x x y 122111 0???βββ。
最新01一元线性回归分析lm
01一元线性回归分析 l m
一元线性回归分析 1一元回归分析 在进行回归分析时,我们必需知道或假定在两个随机之间存在着一定的关系。这种关系可以用Y 的函数的形式表示出来,即Y 是所谓的因变量,它仅仅依赖于自变量X ,它们之间的关系可以用方程式表示。在最简单的情况下,Y 与X 之间的关系是线性关系。用线性函数a+bX 来估计Y 的数学期望的问题称为一元线性回归问题。即,上述估计问题相当于对x 的每一个值,假设bx a y E +=)(,而且,),(~2σbx a N y +,其中a, b, σ2都是未知参数,并且不依赖于x 。对y 作这样的正态假设,相当于设: ε++=bx a y (3) 其中),0(~2σεN ,为随机误差,a, b, σ2都是未知参数。 这种线性关系的确定常常可以通过两类方法,一类是根据实际问题所对应的理论分析,如各种经济理论常常会揭示一些基本的数量关系;另一种直观的方法是通过Y 与X 的散点图来初步确认。 对于公式(3)中的系数a 、b ,需要由观察值),(i i y x 来进行估 计。如果由样本得到了a ,b 的估计值为b a ?,?,则对于给定的x ,a+bx 的估计为x b a ??+,记作y ?,它也就是我们对y 的估计。方程 x b a y ???+= (4) 称为y 对x 的线性回归方程,或回归方程,其图形称为回归直线。
例1:有一种溶剂在不同的温度下其在一定量的水中的溶解度不同,现测得这种溶剂在温度x 下,溶解于水中的数量y 如下表所示: 这里x 是自变量,y 是随机变量,我们要求y 对x 的回归。 其散点图如下: 2.确定回归系数(应用最小二乘法) 在样本的容量为n 的情况下,我们我们可以得到n 对观察值为 ),(i i y x 。现在我们要利用这n 对观察值来估计参数a ,b 。显然,y 的估计值为: bx a y +=? 在上式中a ,b 为待估计的参数。估计这两个参数的方法有极大
一元线性回归分析实验报告
一元线性回归在公司加班制度中的应用 院(系): 专业班级: 学号姓名: 指导老师: 成绩: 完成时间:
一元线性回归在公司加班制度中的应用 一、实验目的 掌握一元线性回归分析的基本思想和操作,可以读懂分析结果,并写出回归方程,对回归方程进行方差分析、显著性检验等的各种统计检验 二、实验环境 SPSS21.0 windows10.0 三、实验题目 一家保险公司十分关心其总公司营业部加班的程度,决定认真调查一下现状。经10周时间,收集了每周加班数据和签发的新保单数目,x 为每周签发的新保单数目,y 为每周加班时间(小时),数据如表所示 y 3.5 1.0 4.0 2.0 1.0 3.0 4.5 1.5 3.0 5.0 2. x 与y 之间大致呈线性关系? 3. 用最小二乘法估计求出回归方程。 4. 求出回归标准误差σ∧ 。 5. 给出0 β∧与1 β∧ 的置信度95%的区间估计。 6. 计算x 与y 的决定系数。 7. 对回归方程作方差分析。 8. 作回归系数1 β∧ 的显著性检验。 9. 作回归系数的显著性检验。 10.对回归方程做残差图并作相应的分析。
11.该公司预测下一周签发新保单01000 x=张,需要的加班时间是多少? 12.给出0y的置信度为95%的精确预测区间。 13.给出 () E y的置信度为95%的区间估计。 四、实验过程及分析 1.画散点图 如图是以每周加班时间为纵坐标,每周签发的新保单为横坐标绘制的散点图,从图中可以看出,数据均匀分布在对角线的两侧,说明x和y之间线性关系良好。 2.最小二乘估计求回归方程
用SPSS 求得回归方程的系数01,ββ分别为0.118,0.004,故我们可以写出其回归方程如下: 0.1180.004y x =+ 3.求回归标准误差σ∧ 由方差分析表可以得到回归标准误差:SSE=1.843 故回归标准误差: 2= 2SSE n σ∧-,2σ∧=0.48。 4.给出回归系数的置信度为95%的置信区间估计。 由回归系数显著性检验表可以看出,当置信度为95%时:
一元线性回归分析法
一元线性回归分析法 一元线性回归分析法是根据过去若干时期的产量和成本资料,利用最小二乘法“偏差平方和最小”的原理确定回归直线方程,从而推算出a(截距)和b(斜率),再通过y =a+bx 这个数学模型来预测计划产量下的产品总成本及单位成本的方法。 方程y =a+bx 中,参数a 与b 的计算如下: y b x a y bx n -==-∑∑ 222 n xy x y xy x y b n x (x)x x x --==--∑∑∑∑∑∑∑∑∑ 上式中,x 与y 分别是i x 与i y 的算术平均值,即 x =n x ∑ y =n y ∑ 为了保证预测模型的可靠性,必须对所建立的模型进行统计检验,以检查自变量与因变量之间线性关系的强弱程度。检验是通过计算方程的相关系数r 进行的。计算公式为: 22xy-x y r= (x x x)(y y y) --∑∑∑∑∑∑ 当r 的绝对值越接近于1时,表明自变量与因变量之间的线性关系越强,所建立的预测模型越可靠;当r =l 时,说明自变量与因变量成正相关,二者之间存在正比例关系;当r =—1时,说明白变量与因变量成负相关,二者之间存在反比例关系。反之,如果r 的绝对值越接近于0,情况刚好相反。 [例]以表1中的数据为例来具体说明一元线性回归分析法的运用。 表1: 根据表1计算出有关数据,如表2所示: 表2:
将表2中的有关数据代入公式计算可得: 1256750x == (件) 2256 1350y ==(元) 1750 9500613507501705006b 2=-??-?=(元/件) 100675011350a =?-=(元/件) 所建立的预测模型为: y =100+X 相关系数为: 9.011638 10500])1350(3059006[])750(955006[1350 750-1705006r 22==-??-???= 计算表明,相关系数r 接近于l ,说明产量与成本有较显著的线性关系,所建立的回归预测方程较为可靠。如果计划期预计产量为200件,则预计产品总成本为: y =100+1×200=300(元)
一元线性回归分析实验报告
. . . 一元线性回归在公司加班制度中的应用 院(系): 专业班级: 学号姓名: 指导老师: 成绩: 完成时间:
一元线性回归在公司加班制度中的应用 一、实验目的 掌握一元线性回归分析的基本思想和操作,可以读懂分析结果,并写出回归方程,对回归方程进行方差分析、显著性检验等的各种统计检验 二、实验环境 SPSS21.0 windows10.0 三、实验题目 一家保险公司十分关心其总公司营业部加班的程度,决定认真调查一下现状。经10周时间,收集了每周加班数据和签发的新保单数目,x为每周签发的新保单数目,y为每周加班时间(小时),数据如表所示 2.x与y之间大致呈线性关系? 3.用最小二乘法估计求出回归方程。 4.求出回归标准误差σ∧。 5.给出0β∧与1β∧的置信度95%的区间估计。 6.计算x与y的决定系数。 7.对回归方程作方差分析。 8.作回归系数1β∧的显著性检验。 9.作回归系数的显著性检验。 10.对回归方程做残差图并作相应的分析。 x=,需要的加班时间是多少? 11.该公司预测下一周签发新保单01000
12.给出0y的置信度为95%的精确预测区间。 E y的置信度为95%的区间估计。 13.给出()0 四、实验过程及分析 1.画散点图 如图是以每周加班时间为纵坐标,每周签发的新保单为横坐标绘制的散点图,从图中可以看出,数据均匀分布在对角线的两侧,说明x和y之间线性关系良好。 2.最小二乘估计求回归方程
用SPSS 求得回归方程的系数01,ββ分别为0.118,0.004,故我们可以写出其回归方程如下: 0.1180.004y x =+ 3.求回归标准误差σ∧ ANOVA a 模型 平方和 自由度 均方 F 显著性 1 回归 16.682 1 16.682 72.396 .000b 残差 1.843 8 .230 总计 18.525 9 a. 因变量:y b. 预测变量:(常量), x 由方差分析表可以得到回归标准误差:SSE=1.843 故回归标准误差: 2= 2SSE n σ∧-,2σ∧=0.48。 4.给出回归系数的置信度为95%的置信区间估计。
相关分析和一元线性回归分析SPSS报告
相关分析和一元线性回归分析SPSS报告
用下面的数据做相关分析和一元线性回归分析: 选用普通高等学校毕业生数和高等学校发表科技论文数量做相关分析和一元线性回归分析。 一、相关分析 1.作散点图
普通高等学校毕业生数和高等学校发表科技论文数量的相关图 从散点图可以看出:普通高等学校毕业生数和高等学校发表科技论文数量的相关性很大。 2.求普通高等学校毕业生数和高等学校发表科技论文数量的相关系 数
把要求的两个相关变量移至变量中,因为都是定距数据,选择相关系数中的Pearson,点击确定,可以得到下面的结果:
Correlations 普通高等学校毕业生数(万人) 高等学校发表科技论文数量(篇) 普通高等学校毕业生数(万人) Pearson Correlation 1 .998** Sig. (2-tailed) .000 N 14 14 高等学校发表科技论文数量(篇) Pearson Correlation .998** 1 Sig. (2-tailed) .000 N 14 14 **. Correlation is significant at the 0.01 level (2-tailed). 两相关变量的Pearson相关系数=0.0998,表示呈高度正相关;相关系数检验对应的概率P值=0.000,小于显著性水平0.05,应拒绝原假设(两变量之间不具有相关性),即毕业生人数好发表科技论文数之间的相关性显著。 3.求两变量之间的相关性
选择相关系数中的全部,点击确定: Correlations (万人) (篇) Kendall's tau_b (万人) Correlation Coefficient 1.000 1.000** Sig. (2-tailed) . . N 14 14 (篇) Correlation Coefficient 1.000** 1.000 Sig. (2-tailed) . . N 14 14 Spearman's rho (万人) Correlation Coefficient 1.000 1.000** Sig. (2-tailed) . . N 14 14 (篇) Correlation Coefficient 1.000** 1.000 Sig. (2-tailed) . . N 14 14 **. Correlation is significant at the 0.01 level (2-tailed). 注解:两相关变量(毕业生数和发表论文数)的Kendall相关系数=1.000,呈正相关;无相关系数检验对应的概率P值,应接受原假设(两变量之间不具有相关性),即毕业生数与发表论文数之间相关性不显著。 两相关变量(毕业生数和发表论文数)的Spearman相关系数=1.000,呈正相关;无相关系数检验对应的概率P值,应接受原假设(两变量之间不具有相关性),即毕业生数与发表论文数之间相关性不显著。 4.普通高等学校毕业生数和高等学校发表科技论文数量的相关系数
第二节 一元线性回归分析
第二节一元线性回归分析 本节主要内容: 回归是分析变量之间关系类型的方法,按照变量之间的关系,回归分析分为:线性回归分析和非线性回归分析。本节研究的是线性回归,即如何通过统计模型反映两个变量之间的线性依存关系。 回归分析的主要内容: 1.从样本数据出发,确定变量之间的数学关系式; 2.估计回归模型参数; 3.对确定的关系式进行各种统计检验,并从影响某一特定变量的诸多变量中找出 影响显著的变量。 一、一元线性回归模型: 一元线性模型是指两个变量x、y之间的直线因果关系。 理论回归模型: 理论回归模型中的参数是未知的,但是在观察中我们通常用样本观察值估计参数值,通常用分别表示的估计值,即称回归估计模型: 回归估计模型: 二、模型参数估计: 用最小二乘法估计: 【例3】实测某地四周岁至十一岁女孩的七个年龄组的平均身高(单位:厘米)如下表所示
某地女孩身高的实测数据 建立身高与年龄的线性回归方程。 根据上面公式求出b0=80.84,b1=4.68. 三.回归系数的含义 (2)回归方程中的两个回归系数,其中b0为回归直线的启动值,在相关图上变现为x=0时,纵轴上的一个点,称为y截距;b1是回归直线的斜率,它是自变量(x)每变动一个单位量时,因变量(y)的平均变化量。 (3)回归系数b1的取值有正负号。如果b1为正值,则表示两个变量为正相关关系,如果b1为负值,则表示两个变量为负相关关系。 [例题·判断题]回归系数b的符号与相关系数r的符号,可以相同也可以不同。() 答案:错误 解析:回归系数b的符号与相关系数r的符号是相同的 [例题·判断题]在回归直线y c=a+bx,b<0,则x与y之间的相关系数() a.r=0 b.r=1 c.0 R软件一元线性回归分析合金钢强度与碳含量的数据 序号碳含量 /% 合金钢强度 /107pa 1 0.10 42.0 2 0.11 43.0 3 0.12 45.0 4 0.13 45.0 5 0.14 45.0 6 0.15 47.5 7 0.16 49.0 8 0.17 53.0 9 0.18 50.0 10 0.20 55.0 11 0.21 55.0 12 0.23 60.0 这里取碳含量为x是普通变量,取合金钢强度为y是随机变量 使用R软件对以上数据绘出散点图 程序如下: > x=matrix(c(0.1,42,0.11,43,0.12,45,0.13,45,0.14,45,0.15,47.5,0.16,49,0.17,53,0.18,50,0.2,55,0.21, 55,0.23,60),nrow=12,ncol=2,byrow=T,dimnames=list(1:12,c("C","E"))) >outputcost=as.data.frame(x) >plot(outputcost$C,outputcost$E) 0.100.120.140.16 0.180.200.22 4550556 outputcost$C o u t p u t c o s t $E 很显然这些点基本上(但并不精确地)落在一条直线上。 下面在之前数据录入的基础上做回归分析(程序接前文,下同) > lm.sol = lm(E~C,data = outputcost) >summary(lm.sol) 得到以下结果: Call: lm(formula = E ~ C, data = outputcost) Residuals: Min 1Q Median 3Q Max -2.00449 -0.63600 -0.02401 0.71297 2.32451 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 28.083 1.567 17.92 6.27e-09 *** C 132.899 9.606 13.84 7.59e-08 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.309 on 10 degrees of freedom Multiple R-squared: 0.9503, Adjusted R-squared: 0.9454 F-statistic: 191.4 on 1 and 10 DF, p-value: 7.585e-08 由计算结果分析: 实验题目:多元线性回归、异方差、多重共线性 实验目的:掌握多元线性回归的最小二乘法,熟练运用Eviews软件的多元线性回归、异方差、多重共线性的操作,并能够对结果进行相应的分析。 实验内容:习题3.2,分析1994-2011年中国的出口货物总额(Y)、工业增加值(X2)、人民币汇率(X3),之间的相关性和差异性,并修正。 实验步骤: 1.建立出口货物总额计量经济模型: 错误!未找到引用源。(3.1) 1.1建立工作文件并录入数据,得到图1 图1 在“workfile"中按住”ctrl"键,点击“Y、X2、X3”,在双击菜单中点“open group”,出现数据 表。点”view/graph/line/ok”,形成线性图2。 图2 1.2对(3.1)采用OLS估计参数 在主界面命令框栏中输入ls y c x2 x3,然后回车,即可得到参数的估计结果,如图3所示。 图 3 根据图3中的数据,得到模型(3.1)的估计结果为 (8638.216)(0.012799)(9.776181) t=(-2.110573) (10.58454) (1.928512) 错误!未找到引用源。错误!未找到引用源。F=522.0976 从上回归结果可以看出,拟合优度很高,整体效果的F检验通过。但当错误!未找到引用源。=0.05时,错误!未找到引用源。=错误!未找到引用源。2.131.有重要变量X3的t检验不显著,可能存在严重的多重共线性。 2.多重共线性模型的识别 2.1计算解释变量x2、x3的简单相关系数矩阵。 点击Eviews主画面的顶部的Quick/Group Statistics/Correlatios弹出对话框在对话框中输入解释变量x2、x3,点击OK,即可得出相关系数矩阵(同图4)。 相关系数矩阵 图4 由图4相关系数矩阵可以看出,各解释变量相互之间的相关系数较高,证实解释变量之间存在多重共线性。 2.2多重共线性模型的修正 SPSS--回归-多元线性回归模型案例解析!(一) 多元线性回归,主要就是研究一个因变量与多个自变量之间的相关关系,跟一元回归原理差不多,区别在于影响因素(自变量)更多些而已,例如:一元线性回归方程 为: 毫无疑问,多元线性回归方程应该 为: 上图中的 x1, x2, xp分别代表“自变量”Xp截止,代表有P个自变量,如果有“N组样本,那么这个多元线性回归,将会组成一个矩阵,如下图所示: 那么,多元线性回归方程矩阵形式为: 其中:代表随机误差, 其中随机误差分为:可解释的误差与不可解释的误差,随机误差必须满足以下四个条件,多元线性方程才有意义(一元线性方程也一样) 1:服成正太分布,即指:随机误差必须就是服成正太分别的随机变量。 2:无偏性假设,即指:期望值为0 3:同共方差性假设,即指,所有的随机误差变量方差都相等 4:独立性假设,即指:所有的随机误差变量都相互独立,可以用协方差解释。 今天跟大家一起讨论一下,SPSS---多元线性回归的具体操作过程,下面以教程教程数据为例,分析汽车特征与汽车销售量之间的关系。通过分析汽车特征跟汽车销售量的关系,建立拟合多元线性回归模型。数据如下图所示: 点击“分析”——回归——线性——进入如下图所示的界面: 将“销售量”作为“因变量”拖入因变量框内, 将“车长,车宽,耗油率,车净重等10个自变量拖入自变量框内,如上图所示,在“方法”旁边,选择“逐步”,当然,您也可以选择其它的方式,如果您选择“进入”默认的方式,在分析结果中,将会得到如下图所示的结果:(所有的自变量,都会强行进入) 如果您选择“逐步”这个方法,将会得到如下图所示的结果:(将会根据预先设定的“F统计量的概率值进行筛选,最先进入回归方程的“自变量”应该就是跟“因变量”关系最为密切, 相关分析和一元线性回归分析S P S S报告 Document number:NOCG-YUNOO-BUYTT-UU986-1986UT 用下面的数据做相关分析和一元线性回归分析: 选用普通高等学校毕业生数和高等学校发表科技论文数量做相关分析和一元线性回归分析。 一、相关分析 1.作散点图 普通高等学校毕业生数和高等学校发表科技论文数量的相关图 从散点图可以看出:普通高等学校毕业生数和高等学校发表科技论文数量的相关性很大。 2.求普通高等学校毕业生数和高等学校发表科技论文数量的相关系数 把要求的两个相关变量移至变量中,因为都是定距数据,选择相关系数中的Pearson,点击确定,可以得到下面的结果: Correlations 普通高等学校毕业生数(万人) 高等学校发表科技论文数量(篇) 普通高等学校毕业生数(万人) Pearson Correlation 1 .998** Sig. (2-tailed) .000 N 14 14 高等学校发表科技论文数量(篇) Pearson Correlation .998** 1 Sig. (2-tailed) .000 N 14 14 **. Correlation is significant at the level (2-tailed). 两相关变量的Pearson相关系数=,表示呈高度正相关;相关系数检验对应的概率P值=,小于显着性水平,应拒绝原假设(两变量之间不具有相关性),即毕业生人数好发表科技论文数之间的相关性显着。 3.求两变量之间的相关性 选择相关系数中的全部,点击确定: Correlations (万人) (篇) Kendall's tau_b (万人) Correlation Coefficient ** Sig. (2-tailed) . . N 14 14 (篇) Correlation Coefficient ** Sig. (2-tailed) . . N 14 14 Spearman's rho (万人) Correlation Coefficient ** Sig. (2-tailed) . . N 14 14 (篇) Correlation Coefficient ** Sig. (2-tailed) . . N 14 14 **. Correlation is significant at the level (2-tailed). 注解:两相关变量(毕业生数和发表论文数)的Kendall相关系数=,呈正相关;无相关系数检验对应的概率P值,应接受原假设(两变量之间不具有相关性),即毕业生数与发表论文数之间相关性不显着。 两相关变量(毕业生数和发表论文数)的Spearman相关系数=,呈正相关;无相关系数检验对应的概率P值,应接受原假设(两变量之间不具有相关性),即毕业生数与发表论文数之间相关性不显着。 4.普通高等学校毕业生数和高等学校发表科技论文数量的相关系数 将所求变量移至变量,将控制变量移至控制中,选中显示实际显着性水平,点击确定: Correlations 普通高等学校毕业生数(万人) 高等学校发表科技论文数量(篇) 普通高等学校毕业生数(万人) Pearson Correlation 1 .998** Sig. (2-tailed) .000 N 14 14 高等学校发表科技论文数量Pearson Correlation .998** 1 一元线性回归分析及方差分析与显著性检验 某位移传感器的位移x 与输出电压y 的一组观测值如下:(单位略) 设x 无误差,求y 对x 的线性关系式,并进行方差分析与显著性检验。 (附:F 0。10(1,4)=,F 0。05(1,4)=,F 0。01(1,4)=) 回归分析是研究变量之间相关关系的一种统计推断法。 一. 一元线性回归的数学模型 在一元线性回归中,有两个变量,其中 x 是可观测、可控制的普通变量,常称它为自变量或控制变量,y 为随机变量,常称其为因变量或响应变量。通过散点图或计算相关系数判定y 与x 之间存在着显著的线性相关关系,即y 与x 之间存在如下关系: (1) / 通常认为 且假设与x 无关。将观测数据 (i=1,……,n)代入(1) 再注意样本为简单随机样本得: (2) 称(1)或(2)(又称为数据结构式)所确定的模型为一元(正态)线性回归模型。 对其进行统计分析称为一元线性回归分析。 模型(2)中 EY= ,若记 y=E(Y),则 y=a+bx,就是所谓的一元线性回归方程, 其图象就是回归直线,b 为回归系数,a 称为回归常数,有时也通称 a 、b 为回归系数。 设得到的回归方程 bx b y +=0? 残差方程为N t bx b y y y v t t t i ,,2,1,?0 =--=-= 根据最小二乘原理可求得回归系数b 0和b 。 对照第五章最小二乘法的矩阵形式,令 ¥ ?????? ? ??=??? ? ??=??? ???? ??=??????? ??=N N N v v v V b b b x x x X y y y Y 2102121?111 则误差方程的矩阵形式为R软件一元线性回归分析(非常详细)
多元线性回归实验报告
多元线性回归实例分析报告
相关分析和一元线性回归分析SPSS报告
一元线性回归,方差分析,显著性分析
