峰度
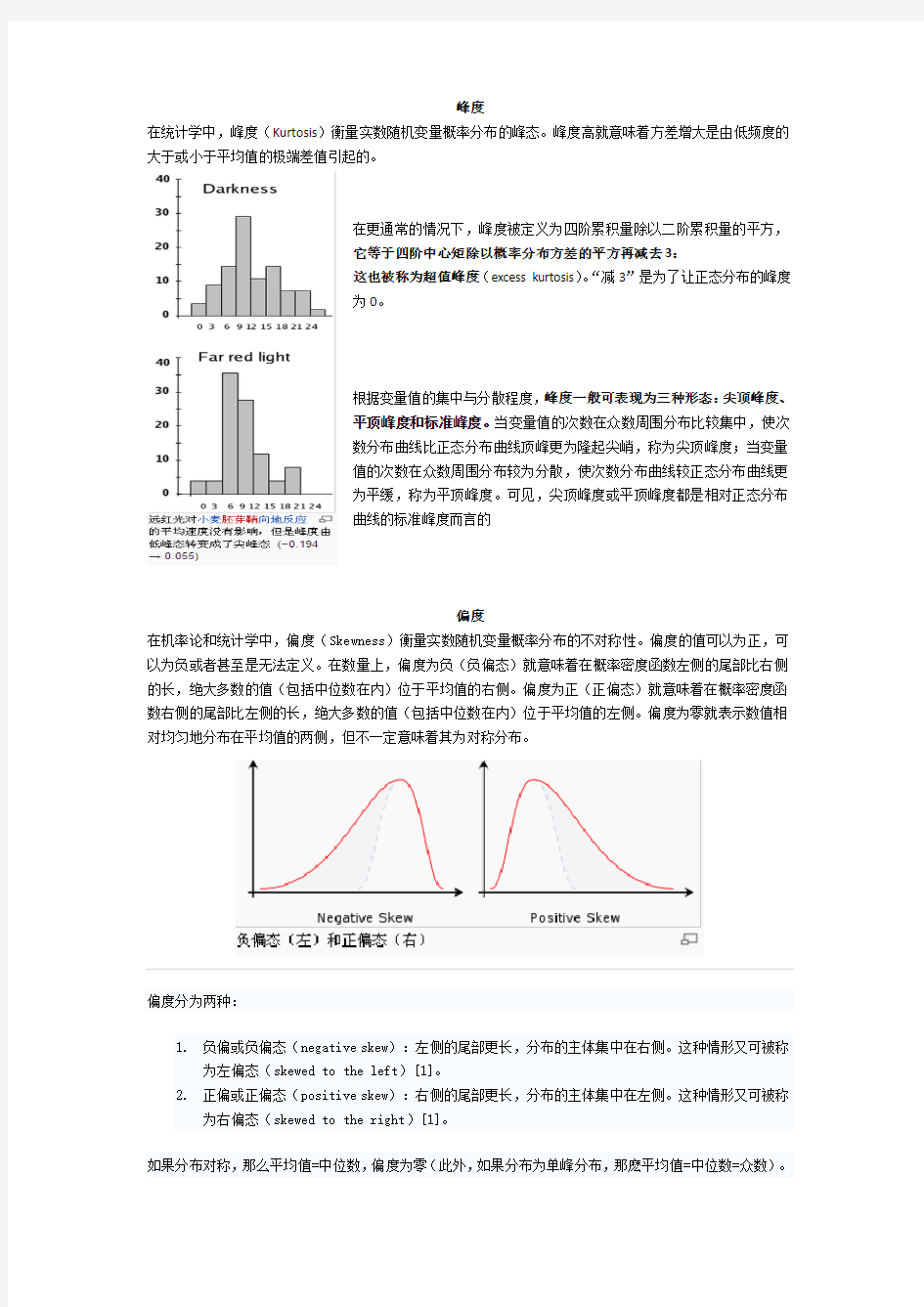

峰度
在统计学中,峰度(Kurtosis)衡量实数随机变量概率分布的峰态。峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。
在更通常的情况下,峰度被定义为四阶累积量除以二阶累积量的平方,
它等于四阶中心矩除以概率分布方差的平方再减去3:
这也被称为超值峰度(excess kurtosis)。“减3”是为了让正态分布的峰度
为0。
根据变量值的集中与分散程度,峰度一般可表现为三种形态:尖顶峰度、
平顶峰度和标准峰度。当变量值的次数在众数周围分布比较集中,使次
数分布曲线比正态分布曲线顶峰更为隆起尖峭,称为尖顶峰度;当变量
值的次数在众数周围分布较为分散,使次数分布曲线较正态分布曲线更
为平缓,称为平顶峰度。可见,尖顶峰度或平顶峰度都是相对正态分布
曲线的标准峰度而言的
偏度
在机率论和统计学中,偏度(Skewness)衡量实数随机变量概率分布的不对称性。偏度的值可以为正,可以为负或者甚至是无法定义。在数量上,偏度为负(负偏态)就意味着在概率密度函数左侧的尾部比右侧的长,绝大多数的值(包括中位数在内)位于平均值的右侧。偏度为正(正偏态)就意味着在概率密度函数右侧的尾部比左侧的长,绝大多数的值(包括中位数在内)位于平均值的左侧。偏度为零就表示数值相对均匀地分布在平均值的两侧,但不一定意味着其为对称分布。
偏度分为两种:
1.负偏或负偏态(negative skew):左侧的尾部更长,分布的主体集中在右侧。这种情形又可被称
为左偏态(skewed to the left)[1]。
2.正偏或正偏态(positive skew):右侧的尾部更长,分布的主体集中在左侧。这种情形又可被称
为右偏态(skewed to the right)[1]。
如果分布对称,那么平均值=中位数,偏度为零(此外,如果分布为单峰分布,那麽平均值=中位数=众数)。
标准误差
标准误差(Standard error),也称均方根误差(Root mean squared error),在相同测量条件下进行的测量称为等精度测量,例如在同样的条件下,用同一个游标卡尺测量铜棒的直径若干
次,这就是等精度测量。对于等精度
测量来说,还有一种更好的表示误差
的方法,就是标准误差。
标准误差定义为各测量值误差的
平方和的平均值的平方根,故又称为
均方误差。
标准误差不仅是一组测量中各个
测量值的函数,而且对一组测量中的
较大误差或较小误差比较敏感,故它是表示准确度的较好方法。
样本均值通常也是该统计总量(population)的均值。但是,来自同一总量的不同样本可能有不同的平均数。其标准平均误差(SEM,即用样本均值作为总体均值估计方法)可以用标准误来衡量;此外,标准误差也可通过计算样本数据,作为标准差的估计方法。
标准误差的理念原自一个事实:只要样本平均值是无偏估计值(unbiased estimator),误差(估量与真实数值的差)的标准差等于估量自身的标准差,因为随机变量和期望值之间差异的标准差等于一个随机变量自身的标准差。
在很多实际应用中,标准差的真正值通常是未知的。因此,标准误这个术语通常运用于代表这一未知量的估计。在这些情况下,需要清楚业已完成的和尝试去解决的标准误差仅仅可能是一个估量。然而,这通行上不太可能:人们可能往往采取更好的估量方法,而避免使用标准误,例如采用最大似然或更形式化的方法去测定置信区间。第一个众所周知的方法是在适当条件下可以采用学生t-分布为一个估量平均值提供置信区间。在其他情况下,标准差可以有效地利用于提供一个不确定性空间的示值,但其正式或半正式使用是提供置信区间或测试,并要求样本总量必须足够大。其总量大小取决于具体的数量分析[2]。
需要注意的是,标准误差不是测量值的实际误差,也不是误差范围,它只是对一组测量数据可靠性的估计。标准误差小,测量的可靠性大一些,反之,测量就不大可靠。进一步的分析表明,根据偶然误差的高斯理论,当一组测量值的标准误差为σ时,则其中的任何一个测量值的误差E i有68.3%的可能性是在(-σ,+σ)区间内。
世界上多数国家的物理实验和正式的科学实验报告都是用标准误差评价数据的,现在稍好一些的计算器都有计算标准误差的功能,因此,了解标准误差是必要的。
置信区间
在统计学中,一个概率样本的置信区间(Confidence interval)是对这个样本的某个总体
参数的区间估计。置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度。置信空间给出的是被测量参数的测量值的可信程度,即前面所要求的“一定概率”。这个概率被称为置信水平。举例来说,如果在一次大选中某人的支持率为55%,而置信水平0.95上的置信区间是(50%,60%),那么他的真实支持率有百分之九十五的机率落在百分之五十和百分之六十之间,因此他的真实支持率不足一半的可能性小于百分之五。
四分差
四分差(interquartile range, IQR),又称四分位距。是描述统计学中的一种方法,以确定第三四分位数和第一四分位数的区别(即的差距)[1]。与方差、标准差一样,表示统计资料中各变量分散情形,但四分差更多为一种稳健统计(robust statistic)。
定义
四分差通常是用来构建箱形图,以及对概率分布的简要图表概述。对一个对称性分布数据(其中位数必然等于第三四分位数与第一四分位数的算术平均数),二分之一的四分差等于绝对中位差(MAD)。中位数是聚中趋势的反映[2]。
IQR = Q3 ?Q1
