当前位置：文档库 › 2009年考研数学一试题及答案解析

2009年考研数学一试题及答案解析

2009年全国硕士研究生入学统一考试

数学一试题答案解析

一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.

（1）当0x →时，()sin f x x ax =-与()()2

ln 1g x x bx =-等价无穷小，则

()A 11,6

a b ==-

. ()B 11,6

a b ==

()

C 11,6

a b =-=-.

()D 11,6

a b =-=

【答案】 A

【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小，则

()sin sin 1cos sin lim

lim

()

ln(1)

()

36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx

→→→→→---==-?---洛洛2

sin lim

166x a ax a

b b

a →==-

=-? 3

6a b ∴=- 故排除,B C 。

另外2

1cos lim

3x a ax bx

→--存在，蕴含了1cos 0a ax -→()0x →故 1.

a =排D 。

所以本题选A 。

（2）如图，正方形(){},1,1x y x y ≤≤

四个区域()1,2,3,4k D k =，cos k

k D I y xdxdy =??

，

则{}14

m ax k k I ≤≤=

()

A 1I .

()

B 2I .

()

C 3I .

()

D 4I .

【答案】A

【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。

24,D D 两区域关于x 轴对称，而(,)cos (,)f x y y x f x y -=-=-，即被积函数是关于y 的

奇函数，所以240I I ==;

13,D D 两区域关于y 轴对称，而(,)cos()cos (,)f x y y x y x f x y -=-==，即被积函数是

关于x 的偶函数，所以{}

1(,),012

cos 0x y y x x I y xdxdy ≥≤≤=>??

；

{}

3(,),012

cos 0x y y x x I y xdxdy ≤-≤≤=

.所以正确答案为A.

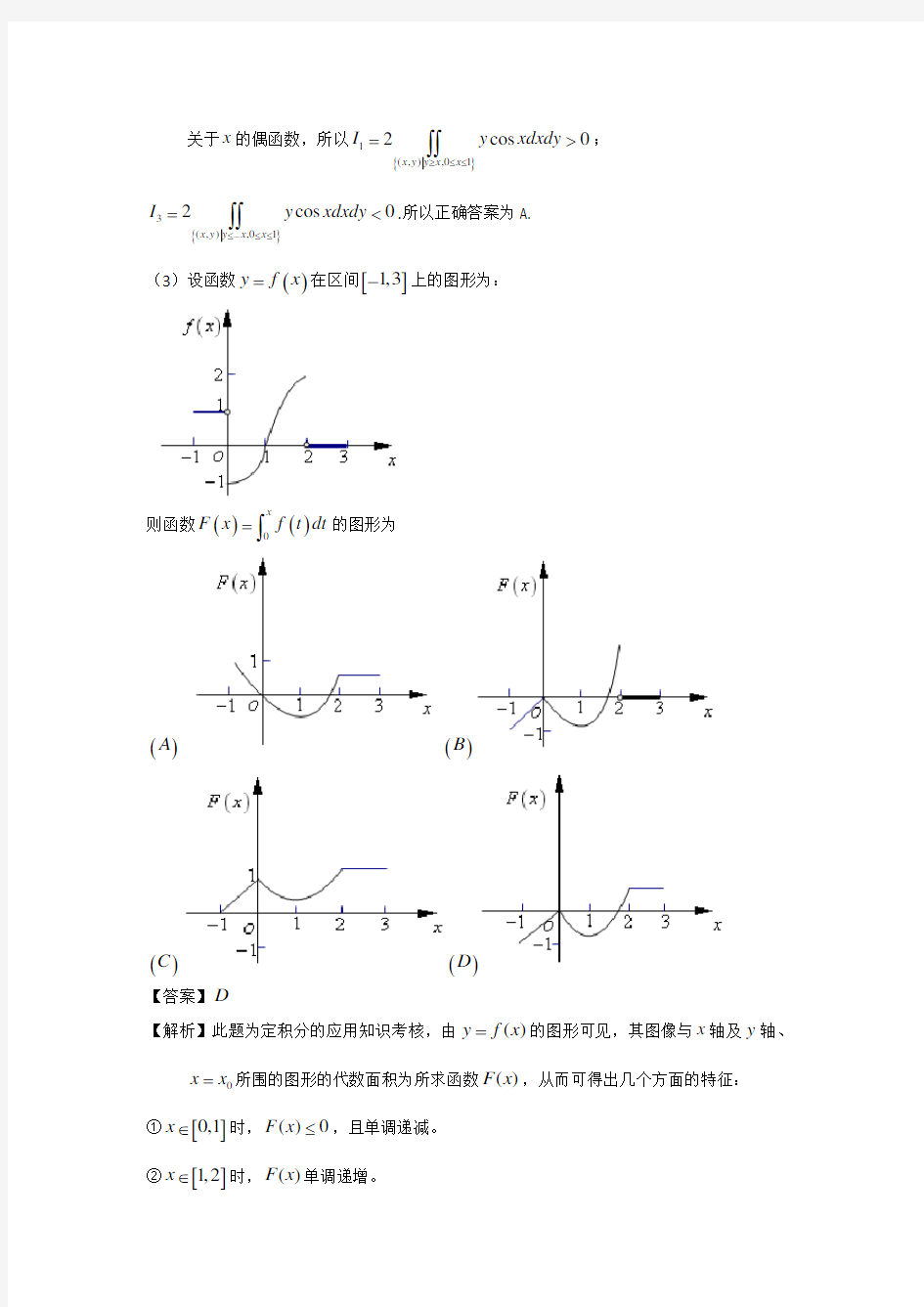
（3）设函数()y f x =在区间[]1,3-上的图形为：

则函数()()0

F x f t dt =

的图形为

()A ()

()

C ()

【答案】D

【解析】此题为定积分的应用知识考核，由()y f x =的图形可见，其图像与x 轴及y 轴、

0x x =所围的图形的代数面积为所求函数()F x ，从而可得出几个方面的特征：

①[]0,1x ∈时，()0F x ≤，且单调递减。 ②[]1,2x ∈时，()F x 单调递增。

③[]2,3x ∈时，()F x 为常函数。

④[]1,0x ∈-时，()0F x ≤为线性函数，单调递增。 ⑤由于F(x)为连续函数

结合这些特点，可见正确选项为D 。

（4）设有两个数列{}{},n n a b ，若lim 0n n a →∞

=，则

()A 当1

n n b ∞=∑收敛时，1

n n n a b ∞

=∑收敛.

()B 当1

n n b ∞=∑发散时，1

n n n a b ∞

=∑发散.

()C 当1

n n b ∞=∑收敛时，221

n a b ∞

=∑收敛.

()D 当1

n n b ∞=∑

发散时，22

n n n a b ∞

=∑发散.

【答案】C 【解析】方法一：

举反例 A 取(1)n

n n a b ==-

B 取1n n a b n ==

D 取1n n a b n

故答案为（C ）方法二：

因为lim 0,n n a →∞

=则由定义可知1,N ?使得1n N >时，有1n a <

又因为1

n n b ∞

=∑收敛，可得lim 0,n n b →∞

=则由定义可知2,N ?使得2n N >时，有1n b <

从而，当12n N N >+时，有2

2n n

n a b b <，则由正项级数的比较判别法可知22

n n n a b ∞

=∑收敛。

（5）设123,,ααα是3维向量空间3R 的一组基，则由基1231

,,2

3ααα到基

122331,,αααααα+++的过渡矩阵为

()A 1012

2003

3?? ? ? ???.

()B 1

23103??

? ???

()C 1112461112461112

6??

? ?

- ? ? ?- ???

()D 11122

114441116

6??- ? ?

?- ?

? ?- ???

. 【答案】A

【解析】因为()()1212,,,,,,n n A ηηηααα= ，则A 称为基12,,,n ααα 到12,,,n

ηηη 的过渡矩阵。

则由基1231

,,2

3ααα到122331,,αααααα+++的过渡矩阵M 满足

()12233112311,,,,2

M ααααααααα??

+++= ??

1231

0111,,2

20230

3ααα????

?= ? ??? ???

所以此题选()A 。

（6）设,A B 均为2阶矩阵，**,A B 分别为,A B 的伴随矩阵，若2,3A B ==，则分块

矩阵O A B

O ??

???

的伴随矩阵为 ()A **

32O B A O ??

???.

()B **

23O B A O ??

???.

()C **

32O A B

O ??

???

()D **

23O A B

O ??

???

. 【答案】B

【解析】根据CC C E *

=，若1

1,C C C C

C C

--*

分块矩阵00A B ??

的行列式22

012360

A A

B B ?=-=?=（）

，即分块矩阵可逆

000

066

000100B B

A A A

B B B

B A

A A **

---*??

???????

?=== ? ? ? ?????

0023

613002

B B A A ***

*?? ?

? ? ???

???

故答案为B 。

（7）设随机变量X 的分布函数为()()10.30.72x F x x -??

=Φ+Φ

???

，其中()x Φ为标准正态分布函数，则EX =

()A 0.

()

B 0.3.

()C 0.7.

()D 1.

【答案】()C

【解析】因为()()10.30.72x F x x -??

=Φ+Φ

???

，所以()()0.7

10.322x F x x -??

'''=Φ+

Φ ???

，所以()()10.30.352x E X xF x dx x x dx +∞+∞-∞

-∞

?-?

??'''=

Φ+Φ ??????

()10.30.352x x x dx x dx +∞+∞-∞

-∞

-??

''=Φ+Φ ???

而()0x x dx +∞-∞

'Φ=?

，()()11221222

x x x dx

u u u du

+∞+∞-∞

-∞

--??''Φ=+Φ= ???

所以00.3520.7E X =+?=。

（8）设随机变量X 与Y 相互独立，且X 服从标准正态分布()0,1N ，Y 的概率分布为

{}{}1012

P Y P Y ====

，记()Z F z 为随机变量Z XY =的分布函数，则函数()

Z F z 的间断点个数为

()A 0.

()B 1. ()C 2.

()D 3.

【答案】 B

【解析】

()()(0)(0)(1)(1)1[(0)(1)]21[(00)(1)]

Z F z P XY z P XY z Y P Y P XY z Y P Y P XY z Y P XY z Y P X z Y P X z Y =≤=≤==+≤===≤=+≤==?≤=+≤=

,X Y 独立 1()[(0)()]2

Z F z P X z P X z ∴=

?≤+≤

（1）若0z <，则1()()2Z F z z =Φ （2）当0z ≥，则1()(1())2Z F z z =

+Φ

0z ∴=为间断点，故选（B ）

二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. （9）设函数(),f u v 具有二阶连续偏导数，(),z f x xy =，则

z x y

?=?? 。

【答案】12

222xf f xyf '''''++ 【解析】

12z f f y x

?''=+??，

22212222z xf f yx f xf f xyf x y

?''''''''''=++?=++??

（10）若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12x

y C C x e =+，则非

齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = 。【答案】2x

y xe x =-++

【解析】由常系数线性齐次微分方程0y ay by '''++=的通解为()12x

y C C x e =+可知

1x y e =，2x

y xe =为其线性无关解。代入齐次方程，有

112

22(1)010[2(1)]020x

y ay by a b e a b y ay by a a b x e a '''++=++=?++='''++=++++=?+=

从而可见2,1a b =-=。

微分方程为''2'y y y x -+=

设特解*y Ax B =+代入，',1y A A ==

220,2

A A x

B x

B B -++

-+==

∴ 特解 *2y x =+

∴ 12()2x y c c x e x =+++

把 (0)2y = ， '(0)0y =代入，得120,1c c ==-

∴ 所求2x

y xe x =-++

（11

）已知曲线(2

:0L y x x =≤≤

，则L

xds =? 。

【答案】

136

【解析】由题意可知，2,,0x x y x x ==≤≤，则

ds =

，

所以()2

148

xds x

11386

（12）设(){}2

,,1x y z x y z Ω=++≤，则2

z dxdydz Ω

=??? 。

【答案】

415

【解析】

方法一：21

222

sin cos z dxdydz d d d ππθ?ρ?ρ?ρ=

????

()21

cos cos d d d π

πθ??ρρ=

cos 1423

515

d π

?π?π=?-

?=?

方法二：由轮换对称性可知2

z dxdydz Ω

???2

x dxdydz Ω

???

y dxdydz Ω

???

所以，()21

11sin 3

3z dxdydz x y z

dxdydz d d r dr π

π?θ?Ω

++=

???????

2214sin sin 3

d r dr d ππ

πππ????=

（13）若3维列向量,αβ满足2T αβ=，其中T α为α的转置，则矩阵T βα的非零特征值为。【答案】2

【解析】2T αβ=

()2T T

βαββαββ∴==?, T

βα∴的非零特征值为2.

(14)设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本，X 和2S 分别为样本均

值和样本方差。若2

X kS +为2np 的无偏估计量，则k =

【答案】1-

【解析】2

X kS + 为2np 的无偏估计 22()E X kX np -

∴+=

(1)1(1)(1)11

n p k n p p n p

k p p k p p k ∴+-

∴+-=∴-=-∴=-

三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.

（15）（本题满分9分）求二元函数()22(,)2ln f x y x y y y =++的极值。【解析】

(,)2(2)0x f x y x y '=+=

(,)2ln 10y f x y x y y '=++=

故10,x y e

= =

2212(2),2,4xx

yy xy

f y f x f xy y

''''''=+ =+ = 则

(0,)

1(0,)

12(2)

0xx e xy e yy

f e

f f e

''=+''=''=

0xx

f ''> 而2()0xy xx yy f f f ''''''-< ∴二元函数存在极小值11(0,)f e e

（16）（本题满分9分）设n a 为曲线n y x =与()1

1,2,.....n y x

n +==所围成区域的面积，记

1221

n n n S a

S a

∞

-===

∑∑，求1S 与2S 的值。

【解析】由题意，n y x =与n+1y=x 在点0x =和1x =处相交，所以1

11111a ()(

)

n n n n x x dx x

n n n n +++=

-=-

++++?，

从而11

111

111S lim

lim (

)lim (

122

+22

n n N N N n n a a N N N ∞

→∞

===

==-

++∑

∑

2211

11111111111=)22+1

2N +1

n n n S a n

n ∞

∞

-===

++-=

+∑

∑

（）（

由2(1)

1(1)

n x

x n

-++-+ ln(1+x)=x- 取1x =得

22111ln(2)1()11ln 22

S S =--+

=-?=-

（17）（本题满分11分）椭球面1S 是椭圆

=绕x 轴旋转而成，圆锥面2S 是过点

()4,0且与椭圆

=相切的直线绕x 轴旋转而成。

（Ⅰ）求1S 及2S 的方程

（Ⅱ）求1S 与2S 之间的立体体积。

【解析】（I ）1S 的方程为

y z ++

=，

过点()4,0与

=的切线为122y x ??

=±- ???

，所以2S 的方程为2

22122y z x ??

+=- ???

。

（II ）记1122

y x =

-，由

，记2y =

则4

22121

1324344V y dx y dx x x dx x dx πππ

π??

=-+-- ?

???

3111143124x x x x x ππ

π???

?=-+--=???????

（18）（本题满分11分）

（Ⅰ）证明拉格朗日中值定理：若函数()f x 在[],a b 上连续，在(,)a b 可导，则存在

(),a b ξ∈，使得()()()()f b f a f b a ξ'-=-

（Ⅱ）证明：若函数()f x 在0x =处连续，在()()0,0δ

>内可导，且()0

lim x f x A +→'=，

则()0f +'存在，且()0f A +'=。

【解析】（Ⅰ）作辅助函数()()()()()()f b f a x f x f a x a b a

?-=--

--，易验证()x ?满足：

()()a b ??=；()x ?在闭区间[],a b 上连续，在开区间()

,a b 内可导，且

()()()()f b f a x f x b a

?-=-

-。

根据罗尔定理，可得在(),a b 内至少有一点ξ，使'

()0?ξ=，即

()f ξ'

()()0,()()()()f b f a f b f a f b a b a

ξ--

=∴-=--

（Ⅱ）任取0(0,)x δ∈，则函数()f x 满足；

在闭区间[]00,x 上连续，开区间()00,x 内可导，从而有拉格朗日中值定理可得：存在

()()0

00,0,x x ξδ∈?，使得()

00()(0)

x f x f f

x ξ

-……()*

又由于()'

lim x f

x A +→=

，对上式（*式）两边取00x +→时的极限可得：

()()00000

0()00lim lim ()lim ()0

x x x x x f x f f f f A x ξξξ+

+++→→→-====-

故'(0)f +存在，且'(0)f A +=。

（19）（本题满分10分）计算曲面积分()

xdydz ydzdx zdxdy

I x

y z

++=

∑

++??

，其中∑

是曲面

224x y z ++=的外侧。

【解析】2

3/2

()

xdydz ydxdz zdxdy

I x y z ∑

++=

++??

，其中222224x y z ++=

2223/22225/2

2(),()()

x y z x

x x y z x y z ?+-=?++++

① 2222

3/2

5/2

2(),()()y

x z y y x y z x y z ?

+-=

?++++②

2223/22225/22(),()()

x y z

z x y z x y z ?

+-=?++++③ ∴①+②+③=

3/2

(

)(

)0()

()

x x y z y x y z z x y z ?

++=?++?++?++

由于被积函数及其偏导数在点（0，0，0）处不连续，作封闭曲面（外侧）

11:.016

x y z R R ∑++=<<

有

3/2

()

134343

xdydz ydxdz zdxdy

x y z R

R dV R

ππ

∑

∑∑Ω

++++=

++=

=??

???

（20）（本题满分11分）设1

111

1104

2A --??

?=- ? ?--?

?，1112ξ-?? ?= ? ?-??

（Ⅰ）求满足2

2131,A A ξξξξ==的所有向量23,ξξ，

（Ⅱ）对（Ⅰ）中的任一向量23,ξξ，证明：123,,ξξξ线性无关。

【解析】（Ⅰ）解方程21A ξξ=

()

1111

111,11110

0000

21104

2202

1100

00A ξ---------??????

=-→→ ? ? ?

? ? ?---?

()2r A =故有一个自由变量，令32x =，由0A x =解得，211,1x x =-= 求特解，令120x x ==，得31x =

故21101021k ξ????

? ?

=-+ ? ? ? ?????

，其中1k 为任意常数

解方程231A ξξ= 2

2202

2044

0A ?? ?=-- ? ??

()

1111022012,22010

00044

0200

00A

ξ-?

? ?-??

? ?

=--→ ? ?

? ?

? ??

故有两个自由变量，令231,0x x =-=，由2

0A x =得11x =

令230,1x x ==，由2

0A x =得10x =

求特解2120

0η??-

?= ? ?

?? 故 3231

102

100

010k k ξ??

- ????? ?

? ?=-++ ? ? ? ? ? ????? ???

，其中23,k k 为任意常数（Ⅱ）证明：由于 121213121212211313

112

1112(21)()2()(21)2

k k k k k k k k k k k k k k k k k k ----=+++-

-+--+

102

≠

故123,,ξξξ 线性无关.

（21）（本题满分11分）设二次型()()2

1231231323,,122f x x x ax ax a x x x x x =++-+-

（Ⅰ）求二次型f 的矩阵的所有特征值；

（Ⅱ）若二次型f 的规范形为2212y y +，求a 的值。

【解析】（Ⅰ） 010

1111a

A a a ??

?=- ? ?--?

0||01

()

a a E A a a a a λλλλλλλλ-----=

-=--

-+---+

()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}

()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+

=--+--

123,2,1a a a λλλ∴==-=+

（Ⅱ）若规范形为22

12y y +，说明有两个特征值为正，一个为0。则

1) 若10a λ==，则 220λ=-< ，31λ= ，不符题意 2) 若20λ= ，即2a =，则120λ=>，330λ=>，符合

3) 若30λ= ，即1a =-，则110λ=-< ，230λ=-<，不符题意综上所述，故2a =

（22）（本题满分11分）

袋中有1个红色球，2个黑色球与3个白球，现有放回地从袋中取两次，每次取一球，以

,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数。

（Ⅰ）求{}10P X Z ==；

（Ⅱ）求二维随机变量(),X Y 的概率分布。

【解析】（Ⅰ）在没有取白球的情况下取了一次红球，利用压缩样本空间则相当于只有1个红球，2个黑球放回摸两次，其中摸了一个红球 1

324(10)9

C P X Z C C

?∴===

（Ⅱ）X ，Y 取值范围为0，1，2，故 ()()()()()()()()()1

111

2311

1223

6666

1221166

2211

110,0,1,046

12,0,0,1363

11,1,2,10

10,29

1,20,2,20

C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C

C C P X Y C C P X Y P X Y ??====

===

????====

===

???====

===??===

?======

（23）（本题满分11 分）

设总体X 的概率密度为2,0

()0,x xe x f x λλ-?>=??其他

，其中参数(0)λλ>未知，1X ，2X ,…

n X 是来自总体X 的简单随机样本

(Ⅰ)求参数λ的矩估计量；

（Ⅱ）求参数λ的最大似然估计量

【解析】（1）由EX X -

而220

2?x

E X x e

dx X X

λλλ

λ+∞-=

=?=?

为总体的矩估计量

（2）构造似然函数

()()1

211

L ,.....,;;n

i n n

x n

n i i i i x x f x x e

λλλ

=-==∑==??∏∏

取对数1

ln 2ln ln n n

i i i i L n x x λλ===+-∑∑

令

ln 222001n

i n

i i

i i d L n

x d x x

λλ

====?

-=?=

∑∑

∑

故其最大似然估计量为2X

λ''=

2009考研数学三真题及答案解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上. （1）函数3 ()sin x x f x x π-=的可去间断点的个数为 (A)1. (B)2. (C)3. (D)无穷多个. （2）当0x →时，()sin f x x ax =-与2 ()ln(1)g x x bx =-是等价无穷小，则 (A)1a =，16b =-. （B ）1a =，16b =. (C)1a =-，16b =-. （D ）1a =-，1 6 b =. （3）使不等式1sin ln x t dt x t >?成立的x 的范围是 (A)(0,1). (B)(1, )2π . (C)(,)2 π π. (D)(,)π+∞. （4）设函数()y f x =在区间[]1,3-上的图形为则函数()()0 x F x f t dt = ?的图形为 (A) (B)

(C) (D) （5）设,A B 均为2阶矩阵，* ,A B * 分别为,A B 的伴随矩阵，若||2,||3A B ==，则分块矩阵O A B O ?? ???的伴随矩阵为 (A)**32O B A O ?? ???. (B)** 23O B A O ?? ???. (C)**32O A B O ?? ??? . (D)** 23O A B O ?? ??? . （6）设,A P 均为3阶矩阵，T P 为P 的转置矩阵，且100010002T P AP ?? ?= ? ??? ，若1231223(,,),(,,)P Q ααααααα==+，则T Q AQ 为 (A)210110002?? ? ? ???. (B)110120002?? ? ? ???. (C)200010002?? ? ? ??? . (D)100020002?? ? ? ??? . （7）设事件A 与事件B 互不相容，则 (A)()0P AB =. (B)()()()P AB P A P B =. (C)()1()P A P B =-. (D)()1P A B ?=. （8）设随机变量X 与Y 相互独立，且X 服从标准正态分布(0,1)N ，Y 的概率分布为 1{0}{1}2 P Y P Y ==== ，记()z F Z 为随机变量Z XY =的分布函数，则函数()z F Z

2009考研数学一真题及解析

2009年全国硕士研究生入学统一考试数学一试题一、选择题：1～8 小题,每小题4分,共32分. (1) 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则 ( ) (A) 11,6a b ==- . (B) 1 1,6a b ==. (C) 11,6a b =-=-. (D) 1 1,6 a b =-=. (2) 如图,正方形(){} ,1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos k k D I y xdxdy = ??, 则{}14 max k k I ≤≤= ( ) (A) 1I . (B) 2I . (C) 3I . (D) 4I . (3) 设函数()y f x =在区间[]1,3-上的图形为则函数()()0 x F x f t dt = ?的图形为 ( ) (A) (B) -1 -1 1 1 x y 1D 2D 3D 4D

(C) (D) (4) 设有两个数列{}{},n n a b ,若lim 0n n a →∞ =,则 ( ) (A) 当 1n n b ∞ =∑收敛时, 1n n n a b ∞ =∑收敛. (B) 当 1n n b ∞ =∑发散时, 1n n n a b ∞ =∑发散. (C) 当 1 n n b ∞ =∑收敛时, 221 n n n a b ∞ =∑收敛. (D) 当 1 n n b ∞ =∑发散时, 22 1 n n n a b ∞ =∑发散. (5) 设123,,ααα是3维向量空间3 R 的一组基,则由基12311 , ,23 ααα到基 122331,,αααααα+++的过渡矩阵为 ( ) (A) 101220033?? ? ? ??? . (B) 120023103?? ? ? ??? . (C) 1 112461 112461112 4 6??- ? ? ? - ? ? ?- ??? . (D) 1112221 114441116 6 6??- ? ? ?- ? ? ?- ??? . (6) 设,A B 均为2阶矩阵,* * ,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵 O A B O ?? ??? 的伴随矩阵为 ( ) (A) **32O B A O ?? ???. (B) ** 23O B A O ?? ???. (C) **32O A B O ?? ???. (D) ** 23O A B O ?? ??? .

2009年考研数学试题答案与解析(数学一)

2009年考研数学试题答案与解析（数学一）一、选择题：1～8小题，每小题4分，共32分. （1）当0x →时，()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小，则 (A)11,6a b ==-. (B)1 1,6a b ==. (C)11,6a b =-=-. (D)1 1,6 a b =-=. 【答案】 A. 【解析】2 ()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小，则 222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx →→→→→---==-?---洛洛230sin lim 166x a ax a b b ax a →==-=-? 36a b ∴=- 故排除(B)、(C). 另外2 01cos lim 3x a ax bx →--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排除(D). 所以本题选（A ）. （2）如图，正方形 (){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =，cos k k D I y xdxdy = ??，则{}14 max k k I ≤≤= (A)1I . (B)2I . (C)3I . (D)4I . 【答案】 A. 【解析】本题利用二重积分区域的对称性及被积函数的奇偶性. 24,D D 两区域关于x 轴对称，而(,)cos (,)f x y y x f x y -=-=-，即被积函数是关于y 的奇函数，所以240I I ==; 13,D D 两区域关于y 轴对称，而(,)cos()cos (,)f x y y x y x f x y -=-==，即被积函数是关于x 的偶函数，所以{}1(,),012 cos 0x y y x x I y xdxdy ≥≤≤=>?? ； {} 3(,),012 cos 0x y y x x I y xdxdy ≤-≤≤=

2009年考研数学三真题及解析

全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一个选项是符合题目要求的，请把所选项前的字母填在答题纸指定位置上. （1）函数3 ()sin x x f x x π-=的可去间断点的个数为 (A)1. (B)2. (C)3. (D)无穷多个. （2）当0x →时，()sin f x x ax =-与2 ()ln(1)g x x bx =-是等价无穷小，则 (A)1a =，16b =-. （B ）1a =，16b =. (C)1a =-，16b =-. （D ）1a =-，1 6 b =. （3）使不等式1sin ln x t dt x t >?成立的x 的范围是 (A)(0,1). (B)(1, )2π . (C)(,)2 π π. (D)(,)π+∞. （4）设函数()y f x =在区间[]1,3-上的图形为则函数()()0 x F x f t dt = ?的图形为 (A) (B)

2009数学一真题答案解析

2009年全国硕士研究生入学统一考试部分数学一试题答案解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内. （1）当0x →时，()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小，则 ()A 1 1,6a b ==-. ()B 1 1,6a b == . ()C 1 1,6 a b =-=-. ()D 1 1,6 a b =-=. 【答案】 A 【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小，则 222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx →→→→→---==-?---洛洛230sin lim 166x a ax a b b ax a →==-=-? 36a b ∴=- 故排除,B C 。另外201cos lim 3x a ax bx →--存在，蕴含了1cos 0a ax -→()0x →故 1.a =排除D 。所以本题选A 。（2）如图，正方形 (){},1,1x y x y ≤≤ 四个区域()1,2,3,4k D k =，cos k k D I y xdxdy =??，则{}14 max k k I ≤≤= ()A 1I . ()B 2I . ()C 3I . ()D 4I . 【答案】A 【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。 24,D D 两区域关于x 轴对称，而(,)cos (,)f x y y x f x y -=-=-，即被积函数是关于y 的奇函数，所以240I I ==; 13,D D 两区域关于y 轴对称，而(,)cos()cos (,)f x y y x y x f x y -=-==，即被积函数是 x