一维非稳态热传导热源反问题研究

一维非稳态热传导热源反问题研究

摘要

本文是关于热传导的正反问题的研究，即利用偏微分方程中典型热传导方程

t时刻温度分布与热源位置。

求解含有内热源的金属细杆

本文从解偏微分方程出发，由已知条件最终得出温度分布函数及热源位置函数并建立了两个数学模型。

模型一：利用偏微分方程及初始温度分布函数建立了一段时间后的温度分布与热源强度、位置之间的数学模型，最终解出一段时间后长杆上的温度分布。

模型二：通过一类抛物型偏微分方程模型，解决已知初始温度分布函数、一段时候后的温度分布函数及热源强度的确定热源位置和中间任意时刻的温度分布函数。

u x t,即t时刻的温度根据模型一建立偏微分方程组，用分离变量法求解(,)

分布函数，并通过Matlab中的PDE(偏微分方程)工具箱求解偏微分方程组，且使解可视化。

u x T,结合抛物型方程，运用根据模型二依然建立偏微分方程组，通过测得(,)

离散正则法，确定热源位置，并通过论证说明问题的唯一性和确定性，给出反问题的数值解法。最后再简单介绍差分法解决热传导在非稳态导热问题中的应用。

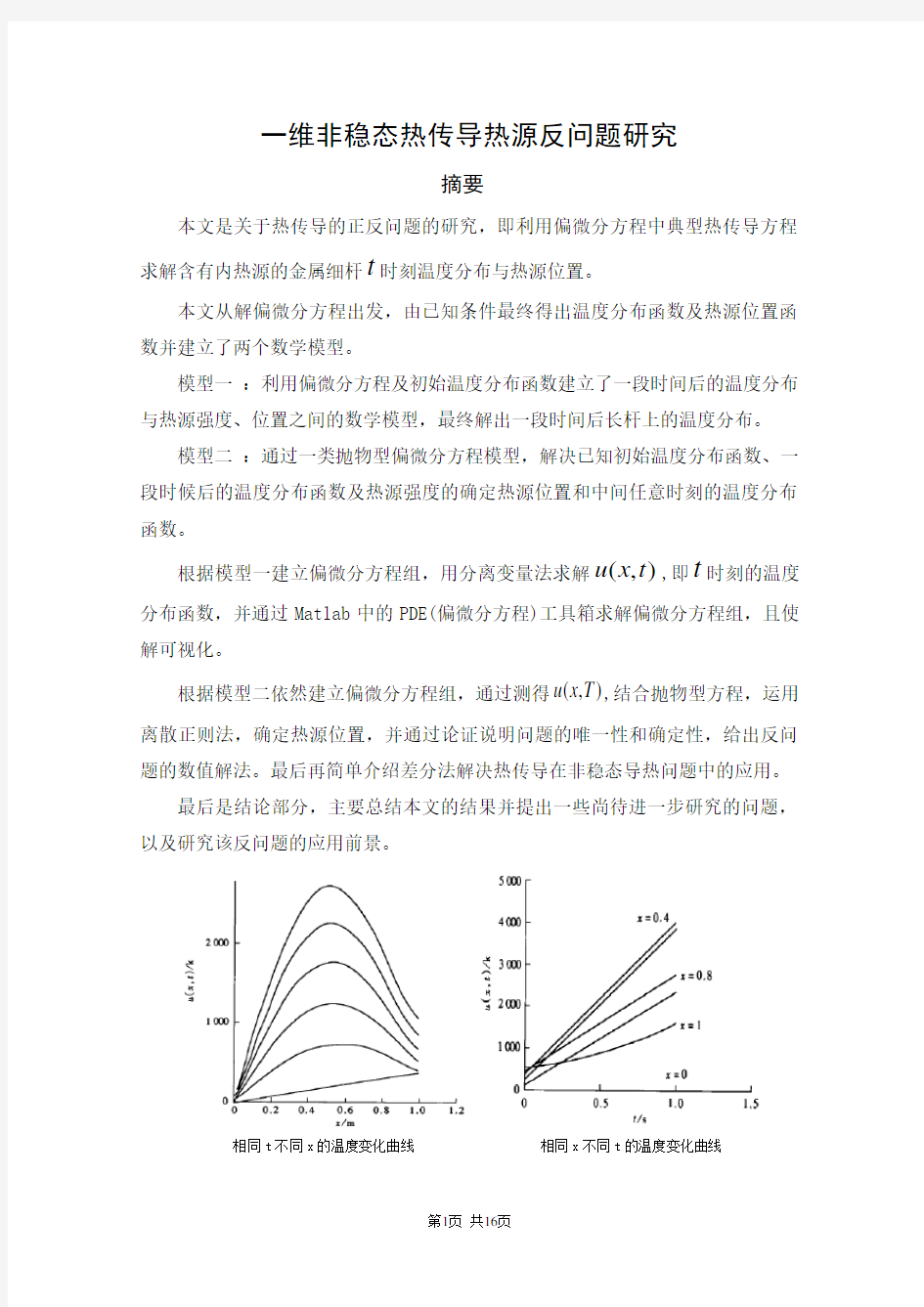
最后是结论部分，主要总结本文的结果并提出一些尚待进一步研究的问题，以及研究该反问题的应用前景。

相同t不同x的温度变化曲线相同x不同t的温度变化曲线

一维非稳态热传导热源反问题研究

一、问题的提出

在金属细秆的传热过程中，温度差是导致其发生必要条件，有无热源决定传导效率的高低。从一维非稳态传导问题的数学模型和初始条件出发，经过对有内热源问题的进一步分析，在初始温度分布已知的情况下，对分布函数的处理显得很关键。对热源反问题的处理中，我们的问题是如何寻找某种合理的附件条件，通过已知方程来解决方程右端的热源的具体位置并使其具有唯一性。本文利用微分方程并建立了满足温度分布的数学物理模型，从理论上导出了温度分布函数和热源位置的求解，并借助计算机软件画出了温度分布图。

二、问题的分析

对于热传导问题，为了使函数解决起来更容易，对于细秆的初始温度分布()

g x我们可以设它在区间[0,L]连续，那么()

g x可以展成正弦或余弦级数，对于有内热源的处理，由于细秆边界条件是齐次的，我们采用叠加原理把一根金属细秆的导热问题分解为有热源的具有其次边界条件的稳态导热问题和一个非稳态

其次问题，则原问题的解为

(,)1(,)2() u x t u x t u x

=+。

对于源反问题的解决有如下3个问题:

1、反问题的唯一性:附加条件给得是否合理，也就是说，这个附加条件是否可以唯一确定热源的具体位置。

2、反问题的稳定性:反演所得到的热源的具体位置，该热源是否是连续地依赖于测量数据()

h t?

3、反问题的数值解法:如何用可行的数值方法反演该热源的具体位置。用离散正则法将温度分布离散化，由已知初始温度分布再利用计算机软件得出热源位置

三、模型假设

1、金属细杆边界与外界无热量交换，即与外界绝缘

2、热源强度在整个时间段里始终保持常量。

3、在求解源反问题时，热源分布相对细杆长度来说，可假设为点热源。

四、符号说明

(,)u x t :温度分布函数，即x 处在t 时刻的温度

(,)f x t ：热源强度

a 2：热扩散系数，单位为m 2/s L ：细杆长度

()g x :初始温度分布函数，即t=0时的杆在x 处温度

其他运算过程中使用符号在步骤中说明，再不赘述。

五、模型的建立与求解

5.1 建立热传导微分方程，并求出温度分布函数(,)u x t

由题意可的模型如下：

2

2

2()u u a f x t x

??=+?? 00 （1） (0,)(,)0u t u L t == 0x ≥ （2）

(,0)()u x g x = 0x L ≤≤ （3）

根据可以把有内热源的非稳态导热问题分解为有热源的具有齐次边界条件的稳态导热问题和一个非稳态齐次问题，即原方程的解为：

(,)1(,)2()u x t u x t u x =+ （4）

式中，

1(,)u x t 是如下非稳态的解：(方程组A)

22

2

11u u a t x ??=?? （A-1）

1(0,)1(,)0u t u l t == （A-2）

1(,0)()2()()u x g x u x p x =-= （A-3）

2()u x 是如下稳态问题的解：（方程组B ）

2

22

2()0u a f x x

?+=? 0

对方程组A:利用分离变量法，假定偏微分方程的解是两个独立变数的乘积，即设

1(,)()()u x t X x Y t =?

代入微分方程（A-1）中，可得

'2''XY a YX = 或

'''

2X Y X a Y

==-λ(λ)为常数 （A-4）（若为+λ，则推导后所得出的解，其结果将对λ取任何值都不能满足边界条件），再由边值条件，有

u1(0,t)=X(0)Y(t)=0 u1(L,t)=X(L)Y(t)=0

必有(0)()0x x L =

=。由（A-4），有

''0X X +λ=；X(0)=X(L)=0 （A-5）；

'20Y a Y +λ= （A-6）；

至此，通过分离变量，我们把微分方程的边值问题转化成为常微分方程的边值问

题。要是(A-5)有非零解，只要取λ=λn =222

n L π（n=1，2，3···）对应的

非零解为sin n x

L

π，类似方程(A-6)的解

2

()()exp((

))n n a Y t Y t t L

π==- 于是得到方程组A 的一组线性无关的解：

2

(,)sin exp(())

n n x n a u x t t L L

ππ=?-

（n=1,2,3···）

通过适当取值，设p(x)是函数sin n x

L π的有限线性组合 即1

()sin N

n

n x p x c L π=∑最终得到

21

(,)sin exp(())N

n n x n a u x t c t L L ππ=-∑ 其中，02()sin L n n x

c p x dx L L π=?

2

121(,)()sin sin exp(())N n x n x n a u x t p x dx t L L L L πππ??=-????

∑

显然，(,)u x t 满足边值条件(,0)

()u x p x =

对方程组B ：即考虑有内热源的情况下，利用傅里叶变换求解

222

2()0u a f x x

?+=? 0

()

2()()F L u x F x x L -=+ 式中，()F x 是21()f x a

-的二次积分。

最后，利用叠加定理将方程组A 与B 合并，即为所建模型温度分布函数的解：

21(,)1(,)2()

2()

()sin sin exp(())()N u x t u x t u x n x n x n a F L p x dx t F x x L L L L L πππ=+-??=-++????

∑

5.2 已知T 时刻的温度分布和初始温度分布，求解热源位置。

对于求源问题，由已知初始温度分布和一段时间后细秆的温度分布，那即为

(,)()u x T f x =来求热源位置。

a 、离散正则化

一维问题的一般提法为：

(,)(,)(,)0,(0,)(,0)()0(0,)()(0,)(0,)(,)0(0,)

t xx x u x t u x t f x x t T u x g x x u t t t T u t u l t t T =+→>∈??=→>??

=ψ→∈??==→∈? （A ）

式中，边界条件

(0,)()(0,)x u t t t T =ψ→∈

当

(,)f x t ，()g x ，()t ψ已知的情况下，原方程变为一维热传导方程的正问题，问

题5.1就是属于一类一维热传导问题，对此借助参考文献[1]得出另一解为：

()0

(,)2(,)()

()(()())t

t

u x t f d k x t g k x t k x t d ∞=

ττ--τψτ+ξ-ξ, ++ξ,ξ

?

?? （B ）

其中，

2

1(,)exp()4x k x t t =-

对于已知

(0,)(u t u l t

==，将其换为附加条件

(0,)(

)u t t t T =φ→<< （C ）

此时根据已知条件，原问题就构成一维热传导方程的寻源反问题，把C 式代入B

式中可得到：

()0

()2(0,)()()(()())t t f d t k t d g k t k t d ∞

ττ=φ+-τψττ-ξ-ξ, +ξ,ξ???

(D)

以下为使用离散正则法解决源反问题： 式（D ）可写成第一类积分算子方程的形式：

,,Af F f Z F U

=∈∈ （E ）

其中，A 为第一类积分算子，Z 为解空间，U 为数据空间。

由于原问题是不适定的，故将积分算子离散化后得到的线性方程组常常是病态的，而且随着维数的增加其病态状况更加严重。这时，直接求解离散方程显然是不行的，必须将其正则化后求解才能得到稳定的近似解。离散正则化的过程可归结如

下：

1)将积分方程离散化得

,,h h h h h h h A f F f W F L =∈∈

其中， h A 为积分算子的离散矩阵；h f 为方程的离散解； h F 为近似数据；h

为离散步长；

2)形成相应的法方程

T h T h h h h A A f A F =

3)法方程的正则化

'()()T

h h h h a a A A C f CF +α=-

其中，C 为单位矩阵；

4)利用偏差原理决定正则参数()a α

=δ，使得((h a φδ))=0，其中δ为

实际数据与测量数据之间的误差，((h h h h

a A f F 2

φδ))=||-||-δ； 5)求得离散正则解

1()()h T T

h a h h h f A A C A F -δ=+α

b 、对离散正则模型进行数值实验（注：本文实验模拟特殊函数借助文献<2>）

设T 时刻细秆的温度分布：T=1，2

()0.00001(1),01T g x x x x =-<<

341

4(exp(1))),01324t t t t t t φ()=-++-<<

4.5

(),01t t T ψ=

<<

则根据拟最优准则<4> 得 345

()325

T t t t F t =

-+

由式E 得22

(1)T f t t =-。在实际应用中，得到的只是一些离散的数据，并且存在着

一定的误差故给()T F t 一个扰动δ作为式E 的右端项()f F t ，应用离散正则化方法来求解()f F t 作为右端项的第一类积分算子方程，求解结果为 ()f f t 。将T f 与()f f t 进

行比较，从而验证离散正则化方法用来求解热传导方程寻反问题的正确性。 C 、寻求源的函数表达式 1)离散第一类积分算子

应用矩形求积公式的和来代替积分的方法对积分算子进行离散，可得到求式E 的近似解的Euler 方法

1

(),i i f i j h f F t -==∑ i =1，2，···，N

其中，

i f 是()f i f t 的近似值，等价的，定义

12((),(),~())N T f f f f N F F t F t F t =

121(,,~)N

T N

N f

f f f R

-=∈

得到下面的矩阵方程

N N N f A f F =

其中，

N A 是一个N N ?的下三角矩阵，其元素依赖于步长h 。

111N

A ?? ?= ?

???

2)由于 N

A 为病态矩阵，并且随着维数的增加，病态特性逐渐增加，应用正则化

方法求解该线性方程组。取T=1，当3

00.01,,10,100N 2-δ=α=δε==时，模拟图

形见图1；当300.01,,10,200N 2-δ=α=δε==时，模拟图形见图2； 图像见附录。 D 、求解热源位置

随机设初始时刻温度分布函数3

()0.0001()T

g x x x =-函数图像：

最大值取的X位置约为0.58处。

五、结果分析与检验（MATLAB模拟与算法）

对问题5.1的偏微分方程组的matlab解法(PDEtools使用)：

(1)用GUI求解。打开PDE Toolbox GUI窗口，在应用模型中选Heat Transfer。

(2)设置坐标的显示范围。单击Options Grid Spacing，在对话框中选择Auto；打开Axes Limits对话框，设置X,Y范围为[0,10]

(3)绘制区域：

设置矩形长8，宽0.5，热源长1，宽0.5，位置任意。并满足默认边界条件的Dirichlet边界条件。

再在PDEmode模式下，分别双击两个区域设置抛物型（Parabolic）Mode参数：矩形区域：密度rho为7.8，比热C为0.465，导热系数k为54（以钢介质为例）热源：rho为1，比热C为0.1，导热系数k为2.热源Q为4，取h=Text=0。

打开Solve Parameters,输入时间向量time为logspace（-2，-1，10）

（4）模拟实现。

a、在plot selection对话框选择color，height（3-d plot）和animation，单击plot，可显示解的动画过程。

b、在plot selection对话框选择color，contour和arrows，单击plot。附截图见附录

对问题5.2有解的结果图，见附录。流程图：

六、模型的优缺点及改进方向

本文采用两个模型，对问题的讨论由正问题到反问题，都给出了详细的推导并进行了严格的数学分析与推导，为使模型建立在坚定数学基础上，模型的建立采用导热微分方程及初始条件得出温度分布和热原位置，对于用离散正则法求源反问题，最后得拟合解用matlab 算法实现；尽管求温度分布函数过于复杂，但在实际应用中，带入实际数据求解也比较容易实现。最后模型给出了求热源位置算法程序流程图。

本模型可以在以下几方面改进： 1）热源强度

(,)f x t 关于位置x 和时间t 都作为变量考虑。

2）如何利用简易的纯数学模型解决热源位置的求解。 3）在实际问题解决中把与外界能量传递考虑进去。

4）为了得到比较通用的解，我们可以将杆两端的温度给非零初值，并设

为常数。

再简单介绍差分法，差分是求解偏微分方程初边值问题的有效的数值方法，广泛应用于传热分析、电磁场分析等工程领域。对于含第一类边界条件的一维热传导混合问题，先建立方程组A,根据方程

,11,1,,()(12)(,)i j i j i j i j u c u u c u tf i j +-+=++-+ 其中，2

2ta c x

=

如果已知j(不同i)坐标每一个格点的温度值，并且由11类边界条件可知两边界 i=l 及i=N 上的温度值，那么就可以求出 +1坐标上每一个格点上的温度值．因此，利用G 式从初始条件j=1开始，就可逐步算出每一个格点上的温度值，运算过程如图1所示．

第一类边界条件下热传导方程的图解

有限差分法绘制的温度分析图像

七、附录：

1、问题5.1解的动画图像

问题5.1的动画过程

温度T和矢量线-grad（T）

问题5.1的生成图像的M文件：

function pdemodel

[pde_fig,ax]=pdeinit;

pdetool('appl_cb',9);

set(ax,'DataAspectRatio',[1 1.5 1]);

set(ax,'PlotBoxAspectRatio',[5 3.3333333333333335 1]);

set(ax,'XLim',[0 10]);

set(ax,'YLim',[0 10]);

set(ax,'XTickMode','auto');

set(ax,'YTickMode','auto');

pdetool('gridon','on');

% Geometry description:

pderect([0.98901098901098861 8.9865689865689866 4.99084249084249

4.4963369963369955],'R1');

pderect([3.0158730158730158 4.017094017094017 4.99084249084249 4.5146520146520137],'R2');

set(findobj(get(pde_fig,'Children'),'Tag','PDEEval'),'String','R1+R2')

% Boundary conditions:

pdetool('changemode',0) pdesetbd(9,'dir',1,'1', '0') pdesetbd(8,...

'dir', 1,'1','0') pdesetbd(7, 'dir', 1, '1','0') pdesetbd(3,... 'dir',1,'1', '0') pdesetbd(2,'dir',1,'1','0') pdesetbd(1,'dir',1,... '1','0')

% Mesh generation:

setappdata(pde_fig,'Hgrad',1.3);

setappdata(pde_fig,'refinemethod','regular');pdetool('initmesh')

% PDE coefficients:

pdeseteq(2,'54.0!2.0','0.0!0.0','(1.0)+(0.0).*(0.0)!(4.0)+(0.0).*(0.0) ','(7.8).*(0.465)!(1.0).*(0.1)','logspace(-2,-1,10)','0.0','0.0','[0 100]') setappdata(pde_fig,'currparam',['7.8!1.0 ';'0.465!0.1 ';

'54.0!2.0 ';'1.0!4.0 ';'0.0!0.0 ';'0.0!0.0 '])

% Solve parameters:

setappdata(pde_fig,'solveparam',...

str2mat('0','1000','10','pdeadworst',...

'0.5','longest','0','1E-4','','fixed','Inf'))

% Plotflags and user data strings:

setappdata(pde_fig,'plotflags',[1 1 1 1 1 1 1 1 0 0 1 10 1 0 1 0 0 1]); setappdata(pde_fig,'colstring','');setappdata(pde_fig,'arrowstring','' );

setappdata(pde_fig,'deformstring','');setappdata(pde_fig,'heightstring ','');

% Solve PDE:

pdetool('solve')

问题5.2求解的流程图：

流程图（()k k 2

ηα=?(α)-δ ）

N=100离散解与真实解对照图

N=200离散解与真实解对照图

八、参考文献

[1]章熙明. 传热学. 北京：中国建筑工业出版社. 2001.12

[2]黄荣华. 红外技术及其在工业生产中的应用. 北京：水利水电出版社. 1987

[3]陆君安尚涛等. 偏微分方程的matlab解法. 湖北：武汉大学出版社 2001.8

[4]王明新王晓光. 数学物理方程北京：清华大学出版社 2007.12

一维非稳态导热问题的数值解

一维非稳态导热问题的数 值解 Prepared on 22 November 2020

计算传热学程序报告 题目：一维非稳态导热问题的数值解 姓名： 学号： 学院：能源与动力工程学院 专业：工程热物理 日期：2014年5月25日

一维非稳态导热问题数值解 求解下列热传导问题： 1.方程离散化 对方程进行控制体积分得到： 非稳态项：选取T 随x 阶梯式变化，有 扩散项：选取一阶导数随时间做显示变化，有 进一步取T 随x 呈分段线性变化，有 e P E e x T T x T )()(δ-=??，w W P w x T T x T )()(δ-=?? 整理可以得到总的离散方程为： 2.计算空间和时间步长 取空间步长为： h=L/N 网格Fourier 数为： 2 20x t x t F ??=??=α（小于时稳定） 时间步长为： 3.建立温度矩阵与边界条件 T=ones(N+1,M+1) T(:,1)=Ti(初始条件温度都为0） T(1,:)=To(边界条件x=0处温度为1） T(N+1,:)=Te(边界条件x=L 处温度为0） 4.差分法求解温度 由离散方程可得到：

转化为相应的温度矩阵形式： 5.输入界面 考虑到方程的变量，采用inputdlg函数设置5个输入变量，对这5个变量设置了默认值，如图1所示。在计算中可以改变不同的数值，得到不同的结果，特别注意稳定条件的临界值是。根据设置的默认值，得到的计算结果如图2所示。 图1matlab变量输入界面 图2默认值的计算结果 6.结果分析 根据上面的分析，给出了程序的输入界面，以及默认值状态下的数值解。可以通过改变不同的输入值，得到需要的分析结果，总结出了下面4点结论：（1）取F0=，得到一维非稳态导热结果如下图所示 图2F0=时一维非稳态导热 从图中可以看出，对于长度L=1的细杆，初始时刻t=0时温度为0，边界条件x=0时，T=1,边界条件x=1时，T=0。随着时间的增加，温度从x=0通过导热的形式传递到x=1，不同时刻不同位置杆的温度都不同，并且随着时间的增加，杆的温度也逐渐增加。 （2）取F0=，可以得到不同位置的温度响应曲线，如下图所示 图3F0=时不同x位置处的温度响应 图中红色曲线代表x=位置的温度瞬态响应，黑色曲线代表x=位置的温度瞬态响应，蓝色曲线代表x=位置的温度瞬态响应。从图中可以看出，随着x的增加，曲线与x轴的交点值越大，温度开始传递到该位置的所需的时间越长。

传热学传热学--第三章 第三节 一维非稳态导热问题

传热学--第三章第三节一维非稳态导热问题 §3 — 3 一维非稳态导热的分析解 本节介绍第三类边界条件下：无限大平板、无限长圆柱、球的分析解及应用。如何理解无限大物体，如：当一块平板的长度、宽度>> 厚度时，平板的长度和宽度的边缘向四周的散热对平板内的温度分布影响很少，以至于可以把平板内各点的温度看作仅是厚度的函数时，该平板就是一块“无限大”平板。若平板的长度、宽度、厚度相差较小，但平板四周绝热良好，则热量交换仅发生在平板两侧面，从传热的角度分析，可简化成一维导热问题。 一、无限大平板的分析解 已知：厚度的无限大平板，初温t0，初始瞬间将其放于温度为的流体中，而且> t0，流体与板面间的表面传热系数为一常数。 试确定在非稳态过程中板内的温度分布。 解：如图3-5 所示，平板两面对称受热，所以其内温度分布以其中心截面为对称面。对 于x 0 的半块平板，其导热微分方程：(0

（边界条件） （边界条件） 对偏微分方程分离变量求解得： （3-10 ） 其中离散值是下列超越方程的根，称为特征值。 其中Bi 是以特征长度为的毕渥数。 由此可见：平板中的无量纲过余温度与三个无量纲数有关：以平板厚度一半为特 征长度的傅立叶数、毕渥数及即：（3-12) 二、非稳态导热的正规状况阶段 1 、平板中任一点的过余温度与平板中心的过余温度的关系 前述得到的分析解是一个无穷级数，计算工作量大，但对比计算表明，当Fo>0.2 时，采用该级数的第一项与采用完整的级数计算平板中心温度的误差小于1% ，因此，当Fo>0.2 时，采用以下简化结果：（3-13 ） 其中特征值之值与Bi 有关。 由上式（3-13 ）可知：Fo>0.2 以后平板中任一点的过余温度(x ，τ) 与平板中心的过余温度(0 ，τ)=（τ ）之比为：（3-14 ） 此式反映了非稳态导热过程中一种很重要的物理现象：即当Fo>0.2 以后，虽然(x ，τ) 与（τ ）各自均与τ 有关，但其比值则与τ 无关，而仅取决于几何位置（x/ ）及边界条件（Bi ）。也就是说，初始条件的影响已经消失，无论初始条件分布如何，只要

一维非稳态导热问题的数值解

计算传热学程序报告 题目：一维非稳态导热问题的数值解 姓名： 学号：学院：能源与动力工程学院专业：工程热物理日期：2014年5月25 日

一维非稳态导热问题数值解 求解下列热传导问题: 1. 方程离散化 对方程进行控制体积分得到: 非稳态项：选取T随x阶梯式变化，有扩散项：选取一阶导数随时间做显示变化，有进一步取T随x呈分段线性变化，有 T ()e x T E T P (T \ T P T W ，( )w (x)x ( X) 整理可以得到总的离散方程为: 2. 计算空间和时间步长 取空间步长为: h=L/N 网格Fourier数为： F。一^ —V (小于时稳定) x x 时间步长为： 3. 建立温度矩阵与边界条件 T=o nes(N+1,M+1) T(:,1)=Ti(初始条件温度都为0) T(1,:)=To(边界条件x=0处温度为1) T(N+1,:)=Te(边界条件x=L处温度为0) 4. 差分法求解温度 由离散方程可得到： 转化为相应的温度矩阵形式： 5. 输入界面 考虑到方程的变量，采用inputdlg函数设置5个输入变量，对这5个变量设置了默认值，如图1所示。在计算中可以改变不同的数值，得到不同的结果，特别注意稳定条件的临界值是。根据设置的默认值，得到的计算结果如图2所示。图1matlab变量输入界面 图2 默认值的计算结果

6. 结果分析根据上面的分析，给出了程序的输入界面，以及默认值状态下的数值解。可以通过改变不同的输入值，得到需要的分析结果，总结出了下面4 点结论： （1）取F o=，得到一维非稳态导热结果如下图所示 图2F。二时一维非稳态导热 从图中可以看出，对于长度L=1 的细杆，初始时刻t=0 时温度为0，边界条件 x=0时，T=1,边界条件x=1时，T=0。随着时间的增加，温度从x=0通过导热的形式传递到x=1，不同时刻不同位置杆的温度都不同，并且随着时间的增加，杆的温度也逐渐增加。 （2）取F o=，可以得到不同位置的温度响应曲线，如下图所示 图3F o=时不同X位置处的温度响应 图中红色曲线代表x=位置的温度瞬态响应，黑色曲线代表x=位置的温度瞬态响应，蓝色曲线代表X=位置的温度瞬态响应。从图中可以看出，随着X的增加，曲线与X 轴的交点值越大，温度开始传递到该位置的所需的时间越长。随着x 的增加，温度响应曲线的变化速率越慢，最终的达到的温度也越低。 （3）取F o=，得到不同位置的温度响应曲线如下图所示 图4F o=时不同X位置处的温度响应 图中三条曲线分别是X=，X=，x=位置的温度瞬态响应。与图3的F o=进行对比，两种情况下的F o值不同，F o值越大表明热扩散系数的值越大。从图中可以 看出热扩散系数对于导热的影响，尸0=时，与F o=相比较，各位置开始响应时所需的时间较长，而且各位置响应曲线的变化速率较小，最终的达到的温度也较低，说明了热扩散系数越小，热传导越慢，传递效率越低。 （4）取F o=，得到非稳定的数值解如图所示 图5F o二时一维非稳态导热 图6F o=时不同X位置处的温度响应 从图中可以看出，对于显示格式的离散方程，并不是所有的F o值都能得到有意义的解，必须要求F o＜时才能得到稳定的数值解，当F o＞时，会出现物理上不真实的解。

第三章非稳态导热分析解法

第三章非稳态导热分析解法 本章主要要求： １、重点内容： ① 非稳态导热的基本概念及特点； ② 集总参数法的基本原理及应用； ③ 一维及二维非稳态导热问题。 2 、掌握内容： ① 确定瞬时温度场的方法； ② 确定在一时间间隔内物体所传导热量的计算方法。 3 、了解内容：无限大物体非稳态导热的基本特点。 许多工程问题需要确定：物体内部温度场随时间的变化，或确定其内部温度达某一极限值所需的时间。如：机器启动、变动工况时，急剧的温度变化会使部件因热应力而破坏。因此，应确定其内部的瞬时温度场。钢制工件的热处理是一个典型的非稳态导热过程，掌握工件中温度变化的速率是控制工件热处理质量的重要因素；金属在加热炉内加热时，要确定它在炉内停留的时间，以保证达到规定的中心温度。 §3—1 非稳态导热的基本概念 一、非稳态导热 1 、定义：物体的温度随时间而变化的导热过程称非稳态导热。 2 、分类：根据物体内温度随时间而变化的特征不同分： 1 2 ）物体的温度随时间而作周期性变化 如图 3-1 所示，设一平壁，初值温度 t 0 ，令其左侧的表面温 度突然升高到 并保持不变，而右侧仍与温度为 的空气接触，试分 析物体的温度场的变化过程。 首先，物体与高温表面靠近部分的温度很快上升，而其余部分仍 保持原来的 t 0 。 如图中曲线 HBD ，随时间的推移，由于物体导热温度变化波及范 围扩大，到某一时间后，右侧表面温度也逐渐升高，如图中曲线 HCD 、 HE 、 HF 。 最后，当时间达到一定值后，温度分布保持恒定，如图中曲线 HG （若 λ=const ，则 HG 是直线）。 由此可见，上述非稳态导热过程中，存在着右侧面参与换热与不参 与换热的两个不同阶段。 （ 1 ）第一阶段（右侧面不参与换热） 温度分布显现出部分为非稳态导热规律控制区和部分为初始温度区的混合分布，即：在此阶段物体温度分布受 t 分布的影响较大，此阶段称非正规状况阶段。 （ 2 ）第二阶段，（右侧面参与换热） 当右侧面参与换热以后，物体中的温度分布不受 to 影响，主要取决于边界条件及物性，此时，非稳态导热过程进入到正规状况阶段。正规状况阶段的温度变化规律是本章讨论的重点。 2 ）二类非稳态导热的区别：前者存在着有区别的两个不同阶段，而后者不存在。 3 、特点； 非稳态导热过程中，在与热流量方向相垂直的不同截面上热流量不相等，这是非稳态导热区别于稳态导热的一个特点。

一维非稳态导热的数值计算

传热学C 程序源 二维稳态导热的数值计算 2.1物理问题 一矩形区域，其边长L=W=1，假设区域内无内热源，导热系数为常数，三个边温度为T1=0，一个边温度为T2=1，求该矩形区域内的温度分布。 2.2 数学描述 对上述问题的微分方程及其边界条件为：2222T T 0x y ??+=?? x=0，T=T 1=0 x=1，T=T 1=0 y=0，T=T 1=0 y=1，T=T 2=1 该问题的解析解：112121(1)sin n n n sh y T T n L x n T T n L sh W L ππππ∞=??? ?---????=? ?-????? ??? ∑ 2.3数值离散 2.3.1区域离散 区域离散x 方向总节点数为N ，y 方向总节点数为M ，区域内任一节点用I,j 表示。 2.3.2方程的离散 对于图中所有的内部节点方程可写为：2222,,0i j i j t t x y ??????+= ? ??????? 用I,j 节点的二阶中心差分代替上式中的二阶导数，得： +1,,-1,,+1,,-1222+2+0i j i j i j i j i j i j T T T T T T x y --+= 上式整理成迭代形式：()()22 ,1,-1,,1,-12222+2() 2()i j i j i j i j i j y x T T T T T x y x y ++=++++ (i=2,3……,N-1)，(j=2,3……,M-1) 补充四个边界上的第一类边界条件得：1,1j T T = (j=1,2,3……,M) ,1N j T T = (j=1,2,3……,M) ,1i j T T = (i=1,2,3……,N)

一维非稳态导热通用程序

!*************************************************************** ! 一维非稳态导热通用程序(不变部分) ! This is a general purpose program to solve 1-D diffusion ! problem in the form of: ! ρcdt/dz=1/a(x)d/dx(a(x)Γdt/dx)+s !******************2003.7 revised******************************** !...................Define Variables......................... MODULE VARIABLES INTEGER,PARAMETER::L1=130 REAL,DIMENSION(L1):: X,XF,XM,XP,R,RF,AP REAL,DIMENSION(L1)::AE,AW,CN,T,TA REAL,DIMENSION(L1)::TG,GM,RC INTEGER:: K=1,KM=1,KP=1,OM=1 INTEGER:: JB,JE,KE,KI,KF,KN,KR,KT,LS,MD,M1,M2,NF REAL:: AEC,AI,BE,BI,DF,DS,DT,EP,EX,PW,TU,TM,XE,XI REAL:: A1,A2,T2,TC,SC,SP,RO,TE,DN,LM END !...............................................Main Program........................................... PROGRAM MAIN USE V ARIABLES IMPLICIT NONE INTEGER I OPEN(1,FILE="q.dat") OPEN(2,FILE="temp.dat") NF=1！（求解变量指标） KN=1！（非稳态问题输出局部变量，输出一次加1） TU=0！（当前时间） 150 KT=1！（非线性问题迭代次数） CALL Speci !First to specify the problem CALL Grid!Set up grid points 200 CALL Difsor!Specify the diff-coeff and source term 220 CALL InterOutput!Output intermediate results CALL Coeff!Set up coefficients of discretization equation CALL TDMA!Solve the algebraic equation by TDMA IF(LS.EQ.2.OR.LS.EQ.4) THEN ！（对非线性问题） IF(DF.GT.EP) THEN！（如果最大偏差大于允许值） DO I=1,M1 TA(I)=TA(I)+OM*(T(I)-TA(I))！（采用亚松弛方式将当前解付给上一次迭代值） END DO DF=0！（最大偏差置零）

一维非稳态热传导热源反问题研究

一维非稳态热传导热源反问题研究 摘要 本文是关于热传导的正反问题的研究，即利用偏微分方程中典型热传导方程 t时刻温度分布与热源位置。 求解含有内热源的金属细杆 本文从解偏微分方程出发，由已知条件最终得出温度分布函数及热源位置函数并建立了两个数学模型。 模型一：利用偏微分方程及初始温度分布函数建立了一段时间后的温度分布与热源强度、位置之间的数学模型，最终解出一段时间后长杆上的温度分布。 模型二：通过一类抛物型偏微分方程模型，解决已知初始温度分布函数、一段时候后的温度分布函数及热源强度的确定热源位置和中间任意时刻的温度分布函数。 u x t,即t时刻的温度根据模型一建立偏微分方程组，用分离变量法求解(,) 分布函数，并通过Matlab中的PDE(偏微分方程)工具箱求解偏微分方程组，且使解可视化。 u x T,结合抛物型方程，运用根据模型二依然建立偏微分方程组，通过测得(,) 离散正则法，确定热源位置，并通过论证说明问题的唯一性和确定性，给出反问题的数值解法。最后再简单介绍差分法解决热传导在非稳态导热问题中的应用。 最后是结论部分，主要总结本文的结果并提出一些尚待进一步研究的问题，以及研究该反问题的应用前景。 相同t不同x的温度变化曲线相同x不同t的温度变化曲线

一维非稳态热传导热源反问题研究 一、问题的提出 在金属细秆的传热过程中，温度差是导致其发生必要条件，有无热源决定传导效率的高低。从一维非稳态传导问题的数学模型和初始条件出发，经过对有内热源问题的进一步分析，在初始温度分布已知的情况下，对分布函数的处理显得很关键。对热源反问题的处理中，我们的问题是如何寻找某种合理的附件条件，通过已知方程来解决方程右端的热源的具体位置并使其具有唯一性。本文利用微分方程并建立了满足温度分布的数学物理模型，从理论上导出了温度分布函数和热源位置的求解，并借助计算机软件画出了温度分布图。 二、问题的分析 对于热传导问题，为了使函数解决起来更容易，对于细秆的初始温度分布() g x我们可以设它在区间[0,L]连续，那么() g x可以展成正弦或余弦级数，对于有内热源的处理，由于细秆边界条件是齐次的，我们采用叠加原理把一根金属细秆的导热问题分解为有热源的具有其次边界条件的稳态导热问题和一个非稳态 其次问题，则原问题的解为 (,)1(,)2() u x t u x t u x =+。 对于源反问题的解决有如下3个问题: 1、反问题的唯一性:附加条件给得是否合理，也就是说，这个附加条件是否可以唯一确定热源的具体位置。 2、反问题的稳定性:反演所得到的热源的具体位置，该热源是否是连续地依赖于测量数据() h t? 3、反问题的数值解法:如何用可行的数值方法反演该热源的具体位置。用离散正则法将温度分布离散化，由已知初始温度分布再利用计算机软件得出热源位置 三、模型假设 1、金属细杆边界与外界无热量交换，即与外界绝缘

第三章非稳态导热分析解法

第三章非稳态导热分析解法 本章主要要求： 1、重点内容: ①非稳态导热的基本概念及特点； ②集总参数法的基本原理及应用; ③一维及二维非稳态导热问题。 2 、掌握内容：①确定瞬时温度场的方法； ②确定在一时间间隔内物体所传导热量的计算方法。 ３、了解内容：无限大物体非稳态导热的基本特点。 许多工程问题需要确定:物体内部温度场随时间的变化,或确定其内部温度达某一极限值所需的时间。如：机器启动、变动工况时,急剧的温度变化会使部件因热应力而破坏。因此,应确定其内部的瞬时温度场。钢制工件的热处理是一个典型的非稳态导热过程，掌握工件中温度变化的速率是控制工件热处理质量的重要因素；金属在加热炉内加热时，要确定它在炉内停留的时间，以保证达到规定的中心温度。 §3—１非稳态导热的基本概念 一、非稳态导热 1 、定义:物体的温度随时间而变化的导热过程称非稳态导热。 ２、分类：根据物体内温度随时间而变化的特征不同分: 1 )物体的温度随时间的推移逐渐趋于恒定值，即： 2 )物体的温度随时间而作周期性变化 如图3－1 所示，设一平壁，初值温度ｔ 0 ,令其左侧的表面温 度突然升高到并保持不变,而右侧仍与温度为的空气接触，试分 析物体的温度场的变化过程。 首先，物体与高温表面靠近部分的温度很快上升，而其余部分仍 保持原来的 t ０。 如图中曲线 HＢD ,随时间的推移，由于物体导热温度变化波及范 围扩大,到某一时间后，右侧表面温度也逐渐升高,如图中曲线HCD 、 HE 、ＨＦ。

最后，当时间达到一定值后,温度分布保持恒定,如图中曲线HG （若λ=const ，则ＨG 是直线）。 由此可见,上述非稳态导热过程中,存在着右侧面参与换热与不参 与换热的两个不同阶段。 （１ )第一阶段(右侧面不参与换热) 温度分布显现出部分为非稳态导热规律控制区和部分为初始温度区的混合分布,即：在此阶段物体温度分布受 t 分布的影响较大，此阶段称非正规状况阶段。 ( ２）第二阶段,（右侧面参与换热) 当右侧面参与换热以后,物体中的温度分布不受to 影响,主要取决于边界条件及物性,此时,非稳态导热过程进入到正规状况阶段。正规状况阶段的温度变化规律是本章讨论的重点。 2 )二类非稳态导热的区别:前者存在着有区别的两个不同阶段,而后者不存在。 3 、特点; 非稳态导热过程中,在与热流量方向相垂直的不同截面上热流量不相等，这是非稳态导热区别于稳态导热的一个特点。 原因：由于在热量传递的路径上，物体各处温度的变化要积聚或消耗能量,所以，在热流量传递的方向上。 二、非稳态导热的数学模型 1 、数学模型 非稳态导热问题的求解规定的｛初始条件，边界条件｝下，求解导热微分方程。 2 、讨论物体处于恒温介质中的第三类边界条件问题 在第三类边界条件下,确定非稳态导热物体中的温度变化特征与边界条件参数的关系。 已知:平板厚 2 、初温 to 、表面传热系数ｈ、平板导热系数，将其突然置于温度为的流体中冷却。 试分析在以下三种情况: <<１／h 、>>1/h 、=1/h 时，平板中温度场的变化。 1 ） 1/ｈ<< 因为 1/h 可忽略,当平板突然被冷却时,其表面温度就被冷却到，随着时间

第03次课J-分离变量法在一维非稳态导热问题中的应用

非稳态导热㈠ 分离变量法在一维非稳态导热问题中的应用 一、无限大平壁一维非稳态导热（参考文献[1]PP45-50） 大平壁在等温介质中的冷却：常物性、无内热源、第三类边界条件（见图1）。 图1 令：f t t -=θ，导热微分方程为：0,022 τδθτθx x a ??=?? 初始条件为：()x f x =≤≤=θδτ,0,0；边界条件： δ δθ θ λτδθ τ====??-==??=x x x h x x x x |,0,0|, 0,00 假设解的形式为()()()ττθΓ?=x X x , 则两个常微分方程： 方程(3—2—3)的解是 由下表知，特征方程（3-2-4）的为()()x A x X m m m εcos =， 特征值为方程()λδεεh m m =tan 的正根，范数()()[] λ λεδλεεh h h N m m m +++=22 22 21 则根据()[]() m L m N dx x f A β??= 特征函数 ，得待定常数为： ，其中，εδβ= 二、半无限大物体一维非稳态导热（参考文献[2]PP40-45） 常物性、无内热源、第二、三类边界条件

典型问题：一半无限大物体，∞≤≤x 0，初始温度为F (x)，当时间τ＞0时，x ＝0的边界上以对流方式向温度为零度的介质传输热量，如图2所示。 该问题的数学描述为：

三、多维的齐次问题（参考文献[2]PP49-57） 典型问题：矩形截面的柱体，为二维非稳态导热，材料为常物性，物体内没有内热源，边界条件如图3所示。 τ??=??+??t a y t x t 1222 2， 0 ,00, 0,0042=+??====+??==??=t H y t b y t y t H x t a x x t x 时，时，时，时， ， ()y x F t ,0==时，τ 图3矩形截面柱体的二维非稳态导热 令()()()()τθΓ=y Y x X y x t ,,，分离方程如下： ,0, 0022=+====+''X H dx dX a x A dx dX x X X ） （β， 0,0,00 42=+====+''Y H dy dY b x B Y y Y Y ）（γ， ()()()C e τ γβατ22+-=Γ 上述问题的完全解为：()()()( )τ γβαγβτ2 2,,,,11 n m e y Y x X C y x t n m m mn n +-∞=∞ =∑∑ = 求解待定系数C mn 后，得： ()()()()()()()()()y d x d y x F y Y x X e y Y x X N N y x t a b n m n m m n n m n m ''''''=??∑∑+-∞=∞ =0011,,,,,1,,22γβγβγβττγβα 上式中出现的本征函数、本征值及范数可从表1-2中直接查得，即： ()()x x X m m ββcos ,=， ()( ) 2 22 22222 1H H a H N m m m +++=βββ，且m β为方程()2tan H a m m =ββ的正根： ()()y y X n n γγsin ,=， () () n n n n n n H H b H N +++=222 22 1 γγγ，且n γ为方程()4cot H b n n -=γγ的正根： ()( ) ()()()()()()()y d x d y x F y x y x H H b H H H a H e y x t a x b y n m n m n n n n n m m m n n m ' '''''?? ++++++=? ? ∑∑ ='='+-∞ =∞ =00 2 2222 22 222211 ,sin cos sin cos 4,,2 2γβγβγ γββττ γβα 四、某些非齐次或非线性问题的处理思路 1、线性、齐次多维非稳态热传导问题（参考文献[2]PP57-61） 对线性、齐次多维非稳态热传导问题，可以象一维问题那样，用分离变量法求解，其结果必定是二重 或三重级数，不便于计算和应用。在一定条件下，规则物体中齐次多维非稳态热传导问题的解可以简单地

一维非稳态导热问题的数值解

计算传热学程序报告题目：一维非稳态导热问题的数值解姓名： 学号： 学院：能源与动力工程学院 专业：工程热物理 日期：2014年5月25日

一维非稳态导热问题数值解 求解下列热传导问题： 1.方程离散化 对方程进行控制体积分得到： 非稳态项：选取T 随x 阶梯式变化，有 扩散项：选取一阶导数随时间做显示变化，有 进一步取T 随x 呈分段线性变化，有 e P E e x T T x T )()(δ-=?? ， w W P w x T T x T )()(δ-=?? 整理可以得到总的离散方程为： 2.计算空间和时间步长 取空间步长为： h=L/N 网格Fourier 数为： 220x t x t F ??=??= α（小于0.5时稳定） 时间步长为： 3.建立温度矩阵与边界条件 T=ones(N+1,M+1) T(:,1)=Ti (初始条件温度都为0） T(1,:)=To (边界条件x=0处温度为1） T(N+1,:)=Te (边界条件x=L 处温度为0） 4.差分法求解温度 由离散方程可得到： 转化为相应的温度矩阵形式： 5.输入界面 考虑到方程的变量，采用inputdlg 函数设置5个输入变量，对这5个变量设置了默认值，如图1所示。在计算中可以改变不同的数值，得到不同的结果，特别注意稳定条件的临界值是0.5。根据设置的默认值，得到的计算结果如图2所示。 图1 matlab 变量输入界面

图2 默认值的计算结果 6.结果分析 根据上面的分析，给出了程序的输入界面，以及默认值状态下的数值解。可以通过改变不同的输入值，得到需要的分析结果，总结出了下面4点结论： （1）取F =0.48，得到一维非稳态导热结果如下图所示 图2 F0=0.48时一维非稳态导热从图中可以看出，对于长度L=1的细杆，初始时刻t=0时温度为0，边界条件x=0时，T=1,边界条件x=1时，T=0。随着时间的增加，温度从x=0通过导热的形式传递到x=1，不同时刻不同位置杆的温度都不同，并且随着时间的增加，杆的温度也逐渐增加。 （2）取F =0.48，可以得到不同位置的温度响应曲线，如下图所示 图3 F0=0.48时不同x位置处的温度响应图中红色曲线代表x=0.1位置的温度瞬态响应，黑色曲线代表x=0.2位置的温度瞬态响应，蓝色曲线代表x=0.4位置的温度瞬态响应。从图中可以看出，随着x的增加，曲线与x轴的交点值越大，温度开始传递到该位置的所需的时间越长。随着x的增加，温度响应曲线的变化速率越慢，最终的达到的温度也越低。 （3）取F =0.25，得到不同位置的温度响应曲线如下图所示 图4 F0=0.25时不同x位置处的温度响应图中三条曲线分别是x=0.1，x=0.2，x=0.4位置的温度瞬态响应。与图3 的F 0=0.48进行对比，两种情况下的F 值不同，F 值越大表明热扩散系数 的值 越大。从图中可以看出热扩散系数对于导热的影响，F 0=0.25时，与F =0.48相 比较，各位置开始响应时所需的时间较长，而且各位置响应曲线的变化速率较小， 最终的达到的温度也较低，说明了热扩散系数越小，热传导越慢，传递效率越低。 （4）取F 0= 0.51，得到非稳定的数值解如图所示 图5 F0=0.51时一维非稳态导热 图6 F0=0.51时不同x位置处的温度响应 从图中可以看出，对于显示格式的离散方程，并不是所有的F 值都能得到 有意义的解，必须要求F 0<0.5时才能得到稳定的数值解，当F >0.5时，会出现

传热学上机C程序源答案之一维非稳态导热的数值计算

二维稳态导热的数值计算 2.1物理问题 一矩形区域，其边长L=W=1，假设区域内无内热源，导热系数为常数，三个边温度为T1=0，一个边温度为T2=1，求该矩形区域内的温度分布。 2.2 数学描述 对上述问题的微分方程及其边界条件为：2222T T 0x y ??+=?? x=0，T=T 1=0 x=1，T=T 1=0 y=0，T=T 1=0 y=1，T=T 2=1 该问题的解析解：112121(1)sin n n n sh y T T n L x n T T n L sh W L ππππ∞=??? ?---??? ?=? ?-?? ??? ??? ∑ 2.3数值离散 2.3.1区域离散 区域离散x 方向总节点数为N ，y 方向总节点数为M ，区域内任一节点用I,j 表示。 2.3.2方程的离散 对于图中所有的内部节点方程可写为：2222,,0i j i j t t x y ???? ??+= ? ??????? 用 I,j 节点的二阶中心差分代替上式中的二阶导数，得： +1,,-1,,+1,,-1 2 2 2+2+0i j i j i j i j i j i j T T T T T T x y --+ = 上式整理成迭代形式：()()22 ,1,-1,,1 ,-12222+2()2() i j i j i j i j i j y x T T T T T x y x y ++=++++ (i=2,3……,N-1)，(j=2,3……,M-1) 补充四个边界上的第一类边界条件得：1,1j T T = (j=1,2,3……,M) ,1N j T T = (j=1,2,3……,M) ,1i j T T = (i=1,2,3……,N) ,2i M T T = (i=1,2,3……,N)