Pair correlations and the survival of superconductivity in and around a super-conducting im

a r X i v :c o n d -m a t /0605624v 2 [c o n d -m a t .m e s -h a l l ] 15 F e
b 2007
Pair –correlations and the survival of superconductivity in and around
a super-conducting impurity
Yonatan Dubi
Physics Department,Ben-Gurion University,Beer Sheva 84105,Israel
(Dated:February 6,2008)
The problem of the survival of superconductivity in a small super-conducting grain placed in a metal substrate is addressed.For this aim the pair correlations and super-conducting gap around and inside a negative-U impurity in one and two dimensions is calculated,in a discrete tight-binding model and a continuous https://www.wendangku.net/doc/a29181472.html,ing a mean-?eld decomposition,it is shown that ?nite pairing in the grain develops when the system has a degeneracy between successive number of electron pairs,and thus may oscillate as a function of the chemical potential.For ?nite pairing in the island,pair correlations in the normal part exhibit a cross-over from being long-ranged to exponentially decaying,depending on the strength of interaction in the grain.It is shown analytically that there is a minimal island size under-which pairing vanishes which is di?erent than that given by Anderson’s criterion,and that it scales as a power-law with island size,rather then exponentially as in isolated grains.
PACS numbers:74.81.Bd,73.63.Bd,74.50.+r,81.07.Bc
I.INTRODUCTION
While superconductivity (SC)on the nano-scale has been a long-standing issue,dating back to the seminal work of Anderson 1,only in the last decade has technolog-ical advancement enabled the realization of such systems in experiment 2.Since then,manifestations of SC on the nano-meter scale has been observed not only in isolated grains 3or granule on insulating substrate 4,but also in inhomogeneous SC thin ?lms,where well-separated SC and normal regions have been observed 5.In such hy-brid systems,the proximity between the SC and normal phases gives rise to novel e?ects,mainly manifested in the local density of states (LDOS),which may be directly measured using scanning tunneling microscopy 6.Encouraged by the technological advance,we ask the following question :what would be the properties of an ultra-small SC grain placed on a metallic (or a doped semi-conducting)substrate ?In such a case,would the gap in the grain still obey Anderson’s criteria 1,or will the proximity e?ect yield a new criteria for the destruction of SC in such a grain,as seen in,e.g.thin SC layers at-tached to normal layer 7,8?Furthermore,in such systems one expects that the SC properties of the grain would be strongly a?ected by the properties of the surrounding metal,and that the proximity to a SC grain would gen-erate pair correlations that would impinge on the local properties of the metallic area,such as its LDOS 9.The above question is also interesting form a technological point of view,as Josephson arrays fabricated on metallic or semi-conducting substrate seem to have large techno-logical potential as nano-electrical devices.
In order to examine these issues,a minimal model of a single SC grain placed in a clean metal matrix is studied,by means of a negative-U Hubbard Hamiltonian in which the interactions are con?ned to a small region in space (so-called ”negative-U impurity”).Applying a
Hartree-Fock-Gorkov mean-?eld decomposition 10leads to the Bogoliubov-De-Gennes (BdG)Hamiltonian 11,which serves as a starting point in the calculation.
The e?ect of the proximity between the SC grain and normal area is investigated by numerically solving a tight-binding BdG Hamiltonian in one and two dimen-sions.It is found that the pairing in the grain is strongly a?ected by the chemical potential (i.e.density)of the substrate,and that on the normal area pair-correlations may either be suppressed exponentially away from the impurity or be long-ranged,depending on the value of the attractive interaction in the grain.
The dependence of the gap in the grain on its size is studied using a continuous version of the BdG Hamil-tonian.Solved analytically,the dependence of the gap on island size is found to diminish as a power-law rather than exponential (as in an isolated grain 13),and the min-imal island size under-which SC vanishes in the grain 14is evaluated,and is found to depend on the properties of the substrate.
II.
THE NEGATIVE-U IMPURITY IN THE
TIGHT-BINDING MODEL
Let us start by examining the discrete tight binding model for the negative-U impurity.The model Hamilto-nian is
H =?t ij σ
c ?
iσc jσ?μ iσ
c ?iσc iσ?Uc ?0↑c ?
0↓c 0↓c 0↑,(1)
where t is the hopping element,μis the chemical po-tential and U >0is the attractive interaction,which is
only present in a single site at the origin (the negative-U impurity).By applying the Hartree-Fock-Gorkov decomposition 10the BdG mean-?eld Hamiltonian 11is
obtained,H =?t
ij σ
c ?iσc jσ+
iσ
(?i ?μ)c ?iσc iσ+
?c ?0↑c ?
0↓+H .c .
,
(2)
where ?=?U c ?0↑c ?
0↓ is the pairing potential and
?i =δi 0
σ|U | c ?0σc 0σ /2
=δi 0|U | n 0 /2is the Hartree
shift.This mean-?eld approach is justi?ed by noting that little is known about this system,and hence a prelimi-nary mean-?eld treatment is in place.The importance of maintaining the Hartree shift term,which naturally ap-pears from the derivation of the mean-?eld
Hamiltonian,has been discussed and demonstrated in Ref.12,where a similar decomposition was used to study the properties of a disordered superconducting sample.
Introducing a Bogoliubov transformation one obtains from the Hamiltonian of Eq.(2)the BdG equations 11for the quasi-particle (QP)u (r i )and quasi-hole excitations v (r i ),
?ξ+(?i ?μ)?δi 0
??δi 0??ξ
?(?i ?μ)
u k (r i )
v k (r i )
=E k
u k (r i )
v k (r i ) .(3)
In Eq.(3)?ξu k (r i )=?t ?δu k (r i +?δ)where ?δ=±?x
,±?y and similarly for v k (r i ),and the energies are the QP ex-citation energies E k ≥0.The pairing potential ?and the electron density per site n i are to be determined self-consistently in terms of the QP amplitudes u (r i )and v (r i ),?=|U |
k
u k (0)v ?
k (0),
n i =2
k
|v k (r i )|2.
(4)
The pairing amplitude ?is ?nite only on the negative-U impurity.However,the proximity to the impurity in-duces pair-correlations f i = c ?i ↑c ?
i ↓ even for i =0,that is outside the impurity.
III.RESULTS IN ONE AND TWO DIMENSIONS
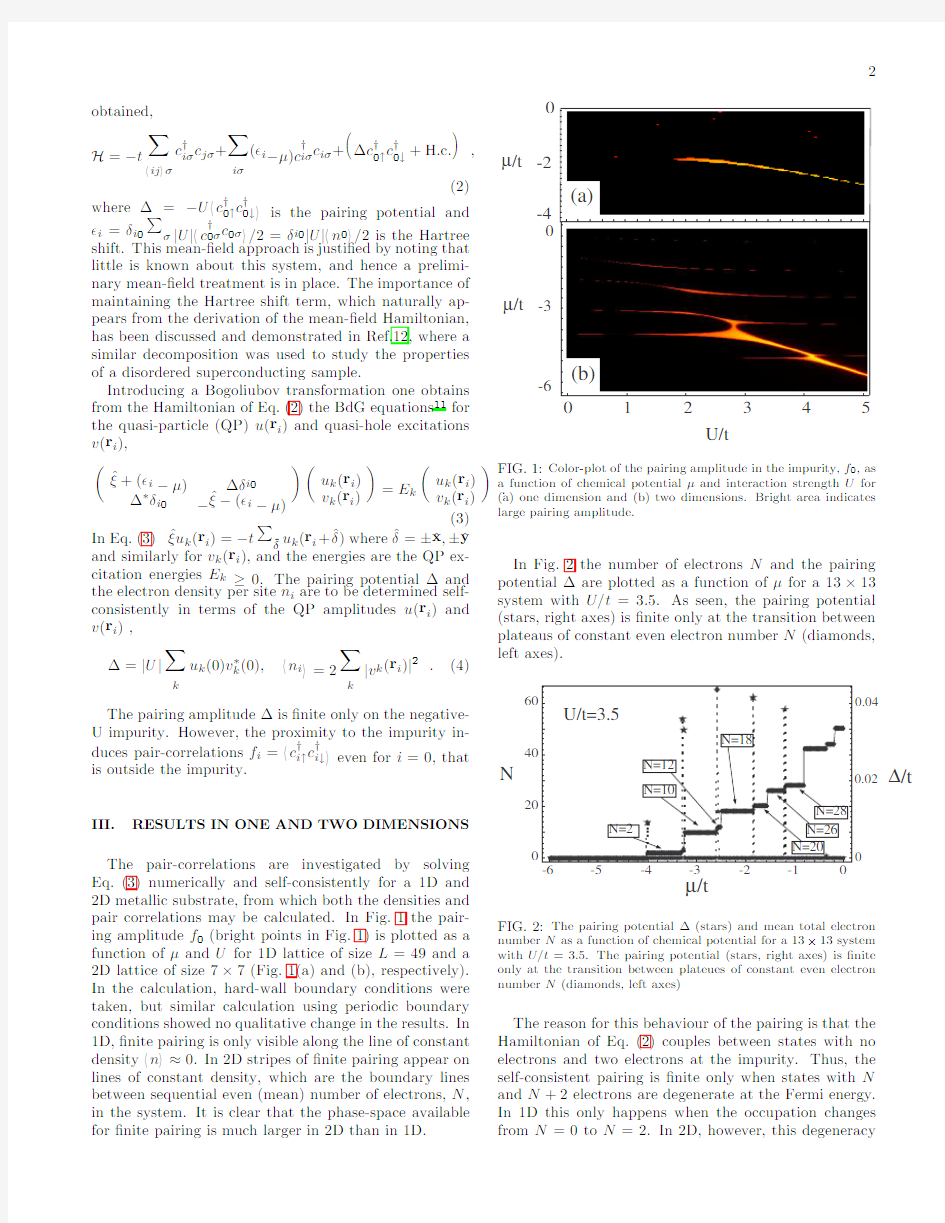
The pair-correlations are investigated by solving Eq.(3)numerically and self-consistently for a 1D and 2D metallic substrate,from which both the densities and pair correlations may be calculated.In Fig.1the pair-ing amplitude f 0(bright points in Fig.1)is plotted as a function of μand U for 1D lattice of size L =49and a 2D lattice of size 7×7(Fig.1(a)and (b),respectively).In the calculation,hard-wall boundary conditions were taken,but similar calculation using periodic boundary conditions showed no qualitative change in the results.In 1D,?nite pairing is only visible along the line of constant density n ≈0.In 2D stripes of ?nite pairing appear on lines of constant density,which are the boundary lines between sequential even (mean)number of electrons,N ,in the system.It is clear that the phase-space available for ?nite pairing is much larger in 2D than in 1D.
-4-2
U/t
μ/t μ/t (b)
(a)
-6
-3
FIG.1:Color-plot of the pairing amplitude in the impurity,f 0,as a function of chemical potential μand interaction strength U for (a)one dimension and (b)two dimensions.Bright area indicates
large pairing amplitude.
In Fig.2the number of electrons N and the pairing
potential ?are plotted as a function of μfor a 13×13system with U/t =3.5.As seen,the pairing potential (stars,right axes)is ?nite only at the transition between plateaus of constant even electron number N (diamonds,left axes).
μ/t
?/t
N
FIG.2:The pairing potential ?(stars)and mean total electron
number N as a function of chemical potential for a 13×13system with U/t =3.5.The pairing potential (stars,right axes)is ?nite only at the transition between plateues of constant even electron number N (diamonds,left axes)
The reason for this behaviour of the pairing is that the Hamiltonian of Eq.(2)couples between states with no electrons and two electrons at the impurity.Thus,the self-consistent pairing is ?nite only when states with N and N +2electrons are degenerate at the Fermi energy.In 1D this only happens when the occupation changes from N =0to N =2.In 2D,however,this degeneracy
is much more common,resulting in many regions of?nite pairing inμ?U phase space,and hence in the oscillatory behaviour shown in Fig.2.We note that while for3D the computation is numerically demanding and will not be presented here,we expect similar behavior,with even more phase space available for SC in the grain.Such a case may be more relevant from the experimental side. Further insight may be gained by studying the depen-dence of?on the interaction strength U.Although from Eq.(4)it would seem that the two are linearly dependent, this is not the case.Due to the Hartree term,U a?ects both the occupation of the impurity and the energy lev-els of the system,pushing the system in and out of the N?N+2degeneracy required for?nite pairing.This is demonstrated in Fig.3,where?(stars,right axes)and N(diamonds,left axes)are plotted as a function of U for a9×9system atμ/t=?2.4.This chemical potential corresponds to a low(≈0.25)electron?lling,which is relevant for a semi-conducting substrate.?(U)is a non-linear(and non-monotonic)function,only?nite above a certain critical interaction U c(μ),in the transition region of N from N=18to N=20.We note that by changing μone may?nd?nite pairing at higher electron densities. However,this is unlikely to occur above half-?lling,as the Hartree term will suppress the pair function in that case.
U/t
N?/t
FIG.3:The pairing potential?(0)and mean total electron num-ber N as a function of interaction strength U for a9×9lattice with μ/t=?2.4,showing that?(U)is a non-monotonic function,only ?nite above U c when N?uctuates between N=18and N=20. Inset:the numerical data(stars)in the region U?U c is?tted with the function?(U)∝(U/U c?1)xΘ(U?U c)(solid line),yielding
x?1/2.
In the region where the pairing in the SC island is ?nite,the proximity e?ect should yield pair correlations
away from the impurity,f i= c?
i↑c?
i↓ .In Fig.4we plot
f i on a chain of length L=5115(normalized to unity) for two values of interaction,U/t=1.5(stars),within the energy band,and U/t=2.5(squares),outside the band.The chemical potential is adjusted for each value of interaction in order to maintain?nite pair correlation in the impurity.When U lies outside the band,it is found that the hole excitations v(n)become localized,resultin
g in an exponential decay of the pair correlations.On the other hand,If U lies within the band the hole excitations are periodic,and generate long-range pair correlations. While this e?ect may be due to the?nite size of the normal system,these long-ranged correlations may have a crucial e?ect16on the global behaviour of a system wit
h many negative-U impurities(so-called dilute negative-U model14,17,18),as they determine the e?ective Josephson coupling between the di?erent impurities.
n
f
(
n
)
/
f
(
)
FIG.4:Spatial structure of the pair correlations f i= c?
i↑
c?
i↓
in a linear chain of length L=51for two values of interaction, U/t=1.5(stars)and U/t=2.5squares.When U lies within the band there are long-range pair-correlations,but an exponential decay of the correlations for U outside the energy band.
IV.TWO DIMENSIONS-CONTINUOUS
MODEL
The starting point for the following calculation is the continuous negative-U Hamiltonian(with =1)
H= σ d2rΨ?σ(r)(?1
4
where ?(r )=|U | Ψ↑(r )Ψ↓(r )is the pairing potential.The Hamiltonian H ?is now expanded with a being a small parameter (speci?cally k F a <<1),
H ?≈
?a 2Ψ?↑(0)Ψ?
↓(0)+H .c .+
(9)+1
π?G r
(r ,r ,?)
where G r (r ,r ′,?)is the retarded Green’s
function,which obeys the
Dyson equation (depicted in Fig.5)
G r (r ,r ′,?)=g r (r ,r ′,?)+?2a 4g r (r ,0,?)×
×g r (0,0,??)G r (0,r ′,?),(10)
=+
=
(a)(b)
+
FIG.5:(a)Dyson’s equation for the single particle Green’s func-tion.(b)Dyson’s equation for the anomalous Green’s function.
Where g r
(r ,r ′
,?)=?iπ?J 0(
π?
γ1+γ
J 0(
?/μ,independent of the pairing potential in the is-land,which only a?ects the depth of the minigap.Due to these oscillations in the LDOS,one expects that the charge density will re-distribute (and also exhibit oscilla-tions)around the SC–semi-conductor interface.One also expects that the density will re-distribute within the SC island.However,this e?ect cannot be probed within the point-island limit (Eq.(10)),and will be discussed in a future study.
Next we turn to a self consistent calculation of ?.Using the Dyson equation for the anomalous Green’s
function F (x,x ′,t )= T ψ?↑(x,0)ψ?↓(x ′
,t ) (Fig.5(b))one ?nds
F (x,x ′
,?)=
?a 2
1+γ
η(x ),(15)
where η(x )= ?
D
??D d ?g (x,0,?)g (0,x,??).At the center
of the impurity η(0)=?2(π?)2?D .Inserting this into Eq.(15)results in an algebraic equation for ?(0),
1=2(π?)2a 2
|U |?D
(π?a 2)2?(0)2π?a 2
2π2?2|U |?D a 2?1 1/2.
(17)
This self-consistent solution vanishes when a =a I =(2π2?2?D |U |)?1/2,which is the minimal island area.Let
us estimate the minimal island size,ξa ~a 1/2
I for a re-alistic system,composed of a Nb island embedded on a semi-conducting quantum-well made of Si or GaAs.Tak-ing the e?ective mass m ?/m =0.98and m ?/m =0.063
for Si and GaAs respectively,20one can estimate the2D-DOS in the quantum well.Taking for Nb T c=9.26K
andθD=275K,21one?nds that for the Nb/Si hybrid the minimal island radius isξI~80nm,and for the Nb/GaAs systemξI~20nm.Both these lengths are still in the point-island regime,since the Fermi wave-length
may be an order of magnitude larger for such quantum wells.
Eq.(17)also supplies us with a dependence of?on the island size and interaction strength.In the inset of Fig.3we plot a?t of the numerical data in the region U?U c(stars)to a function of the form?(U)∝(U/U c?1)xΘ(U?U c)(solid line),as in Eq.(17).The?t yields the exponent x=0.5002,in good agreement with the continuous model.
In the de?nition of the model(Eq.(5)-(7))we have ne-
glected the boundary conditions on the normal-SC inter-face.Omitting the boundary e?ect is hard to justify a-priory,especially when the size of the SC grain is smaller than the SC coherence length.Accounting for the bound-ary should be accounted for by solving Eqs.(13)-(15)with an additional constraint?(a)=0.However,the com-parison between the numerical calculation(in which the boundary condition are inherently implemented)and the analytical result(inset of Fig.3)shows a striking equiv-alence between them.This indicates that neglecting the boundary e?ect merely results in a quantitative modi?ca-tion.It does not change the qualitative behavior,which is mainly characterized by the power-law dependence spec-i?ed in Eq.(17).
V.DISCUSSION
One main feature of the result shown in Eq.(17)is that,in contrast to previous works on the proximity e?ect7,8,14,the length-scale is not the usual supercon-ducting coherence lengthξ,but rather a new length scale a I=(2π2?2?D|U|)?1/2.In order to understand the ori-gin of this new length scale we cast the criterion for the vanishing of SC correlations in the island given by Eq.(17)to the form
|U|
1
2
1P.W.Anderson,J.Phys.Chem.Solids11,26(1050).
2C.T.Black,D.C.Ralph,and M.Tinkham,Phys.Rev.
Lett.76,688(1996);D.C.Ralph,C.T.Black,and M.
Tinkham,Phys.Rev.Lett.78,4087(1996).
3For a review see,e.g.,J.von Delft and D.Ralph,Physics Reports34561,(2001).
4S.Reich,G.Leitus,R.Popovitz-Biro,and M.Schechter, Phys.Rev.Lett.91,147001(2003);W.-H.Li,C.C.Yang,
F.C.Tsao,and K.C.Lee,Phys.Rev.B68,184507(2003);
S.Bose,P.Raychaudhuri,R.Banerjee,P.Vasa,and P.
Ayyub,Phys.Rev.Lett.95,147003(2005).
5T.Cren,D.Roditchev,W.Sacsk and J.Klein,Europhys.
Lett.,54(1),84(2001);S.H.Pan,J.P.O’Neal,R.L.
Badzey,C.Chamon,H.Ding,J.R.Engelbrecht,Z.Wang,
H.Eisaki,S.Uchida,A.K.Gupta,K.-W.Ng,E.W.Hud-
son,https://www.wendangku.net/doc/a29181472.html,ng,J.C.Davis,Nature413,282(2001);
C.Howald,P.Fournier,and A.Kapitulnik,Phys.Rev.B
64,100504(R)(2001);https://www.wendangku.net/doc/a29181472.html,ng,V.Madhavan,J. E.
Ho?man,E.W.Hudson,H.Eisaki,S.Uchida,J.C.Davis, Nature415,412(2002).
6A.C.Fang,L.Capriotti, D.J.Scalapino,S.A.Kivel-son,N.Kaneko,M.Greven,and A.Kapitulnik,Phys.Rev.
Lett.96,17007(2006).
7P.G.de-Gennes,Rev.Mod.Phys.36,225(1964).
8W.L.MacMillan,x.Rev.175,537(1968).
9See,for instance,W.Silvert and L.N.Cooper,x.Rev.
141,336(1966).
10A.A.Abrikosov,L.P.Gorkov,and I.E.Dzyaloshinski, Methods of Quantum Field Theory in Statistical Physics (Dover Publications Inc.,New York,1963).11P.G.de Gennes,Superconductivity in Metals and Alloys (Benjamin,New York,1966).
12A.Ghosal,M.Randeria and N.Trivedi,Phys.Rev.Lett.
81,3940(1998);A.Ghosal,M.Randeria and N.Trivedi, Phys.Rev.B65,14501(2001).
13M.Strongin,R.S.Thompson,O.F.Kammerer,and J.E.
Crow,Phys.Rev.B1,1078(1970).
14B.Spivak,A.Zyuzin and M.Hruska,Phys.Rev.B64, 132502(2001).
15A similar calculation was performed for the2D lattice, yielding a similar result.
16Y.Dubi,Y.meir and Y.Avishay,in preparation.
17G.Litak and B.L.Gyor?y,Phys.Rev.B62,6629(2000). 18D.Hurt,E.Odabashian,W.E.Pickett,R.T.Scalettar,
F.Mondaini,T.Paiva and R.R.dos Santos,Phys.Rev.
B72,144513(2005).
19see,e.g.,review by M.L.Cohen in Superconductivity,R.D.
Parks,Ed.,Vol.2(Marcel Dekker INC.New York1969). 20Handbook series on semiconductor parameters,M.Levin-shtein,S.Rumyantsev and M.Shur,Eds.,Vol.1(World Scienti?c,Singapore1996).
21N.W.Ashcroft and N.D.Mermin,Solid State Physics (Brooks Cole1976).
22P.W.Anderson,Phys.Rev.124,41(1961).
23A.Taraphder and P.Coleman,Phys.Rev.Lett.66,2814 (1991);Y.Matsushita,H.Bluhm,T.H.Geballe and I.R.
Fisher,Phys.Rev.Lett.94,157002(2005);M.Dzero and J.Schmalian,Phys.Rev.Lett.94,157003(2005);
