第五章 非平稳时间序列的随机分析实验报告

第五章非平稳时间序列随机性分析实验报告下表为1948-1981年美国女性（大于20岁）月度失业率数据。

表5-1 1948-1981年美国女性月度失业率

数据来源：Andrews&Herzberg(1985)。

根据以上数据，下面用Eviewis6.0对1948-1981年美国女性（大于20岁）月度失业率数据进行随机性分析。

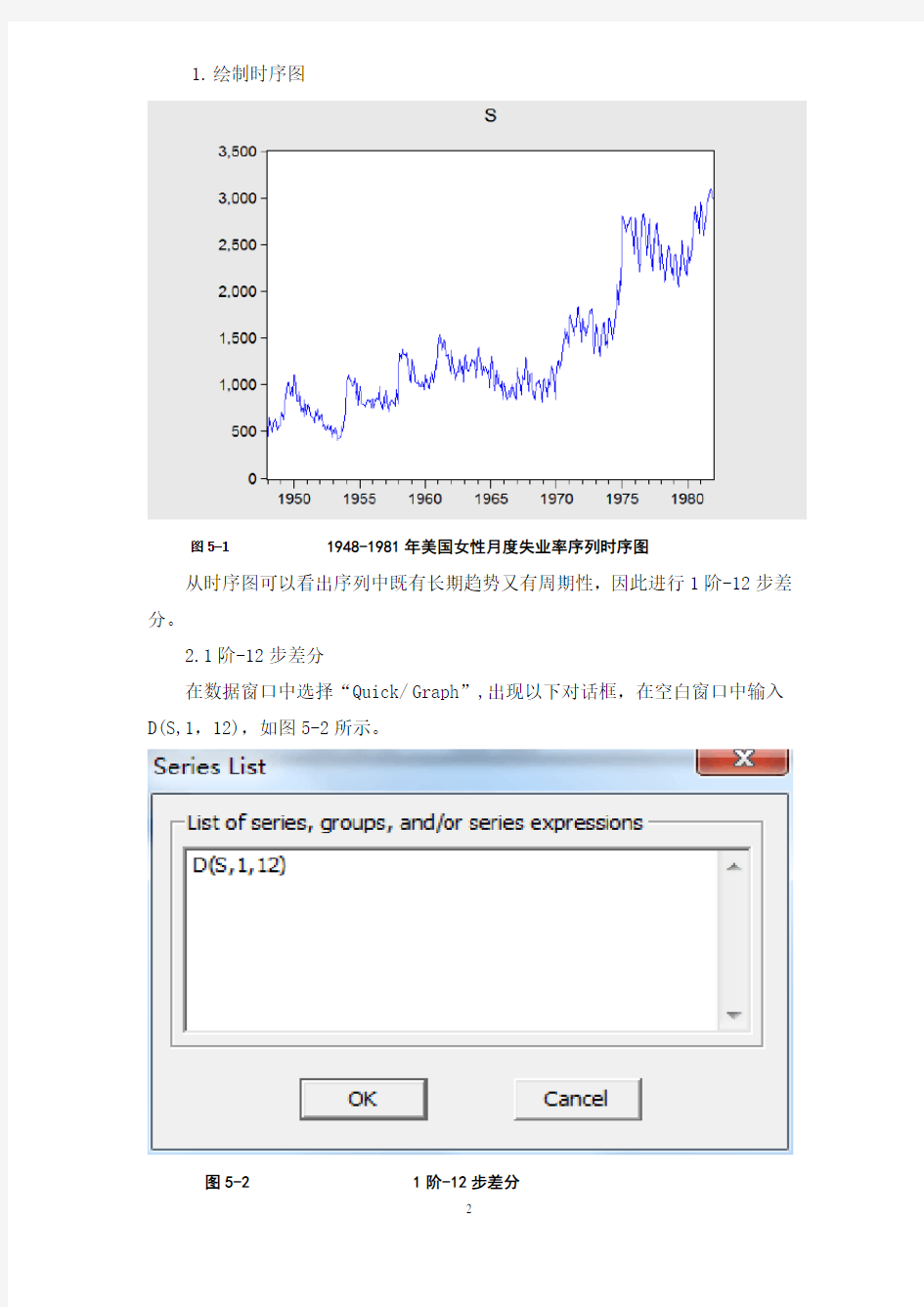
1.绘制时序图

图5-1 1948-1981年美国女性月度失业率序列时序图

从时序图可以看出序列中既有长期趋势又有周期性，因此进行1阶-12步差分。

2.1阶-12步差分

在数据窗口中选择“Quick/Graph”,出现以下对话框，在空白窗口中输入D(S,1，12)，如图5-2所示。

图5-2 1阶-12步差分

图5-3 D(S，1，12) 时序图

从时序图看，D（S,1,12）均值稳定，没有明显测周期性，方差有界；生成序列D1=D(S,1,12)，通过相关分析，具体分析序列的平稳性。如下图所示。

图5-4 D(S，1，12)的相关分析

图5-4中，自相关2阶显著，但是12阶也是显著的，因此在趋势平稳中又包含了周期性因素。以下对其进行ARMA模型分析。

3.ARMA模型拟合

对平稳非白噪声序列D（S,1,12）尝试用ARMA模型拟合。

（1）对序列进行AR模型拟合。在主窗口命令框中输入LS D(S,1，12) AR(1) AR(12)，得到以下回归结果，如图5-5所示，并对其残差相关性进行检验，如图5-6。

图5-5 AR(1，12)模型拟合序列D（S，1，12）

残差相关性检验结果如下图：

图5-6 AR(1,12)模型拟合序列D（S，1，12）的残差相关图

从上图看出模型残差非白噪声，模型提取信息不充分。

（2）对序列进行MA模型拟合。在主窗口命令框中输入LS D(S,1,12) MA(1) MA(12)，得到以下回归结果，如图5-7所示，并对其残差相关性进行检验，如图5-8。

图5-7 MA(1，12)模型拟合序列D（S，1，12）

图5-8 AR(1，12)模型拟合序列D（S，1，12）的残差相关图

从图5-8可以看出模型残差也非白噪声，模型提取信息仍然不充分。

4.乘积季节模型拟合

经过以上分析和ARMA模型拟合，效果不理想。序列中的长期趋势，季节效应和随机波动不能简单分开，故以下对其运用乘积季节模型拟合。

图5-9 ARMA（1，1）×（1，0，1）12拟合序列D(S，1，12)

图5-10 ARMA（1，1）×（1，0，1）12拟合序列D(S，1，12)模型参数

可以看出SAR(12)的参数并不明显，P值为0.9608，因此删除该项，并对序列重新进行模型拟合。

图5-11 ARMA（1，1）×（0，0，1）12拟合序列D(S，1，12)

图5-12 ARMA（1，1）×（0，0，1）12拟合序列D(S，1，12)模型参数

可以看出乘积模型的残差为白噪声序列，其P值显著大于0.05，该模型提取序列的信息充分；参数都显著，因此模型建立成立。

模型的具体形式为：

（1-B ）(1-B 12)S=ε)8273.01(6829.015652.0112B B

B

++-

将序列拟合值与序列观察值联合作图，可以直观地看出该乘积模型对原序列的拟合效果良好。

图5-13 美国女性月度失业率序列拟合效果图

附表：以下是建立模型具体分析过程中产生的表格。

备表1 D（S，1，12）的相关分析

Date: 06/15/14 Time: 09:13

Sample: 1948M01 1981M12

Included observations: 395

Autocorrelation Partial Correlation AC PAC Q-Stat Prob

*|. | *|. | 1 -0.138 -0.138 7.5961 0.006 .|* | .|* | 2 0.189 0.173 21.878 0.000 .|. | .|. | 3 0.022 0.071 22.076 0.000 .|. | .|. | 4 0.061 0.041 23.545 0.000 .|. | .|. | 5 0.011 0.007 23.593 0.000 .|. | .|. | 6 0.052 0.036 24.692 0.000 *|. | *|. | 7 -0.082 -0.084 27.401 0.000 .|. | .|. | 8 0.043 0.003 28.133 0.000 .|. | .|. | 9 -0.013 0.018 28.198 0.001 *|. | *|. | 10 -0.128 -0.140 34.862 0.000 .|. | .|. | 11 0.068 0.042 36.770 0.000 ***|. | ***|. | 12 -0.454 -0.429 121.08 0.000 .|. | *|. | 13 0.041 -0.073 121.79 0.000 .|. | .|* | 14 -0.041 0.119 122.47 0.000 *|. | .|. | 15 -0.081 -0.042 125.19 0.000 .|. | .|. | 16 -0.058 -0.032 126.59 0.000 .|. | .|. | 17 0.034 0.043 127.08 0.000 *|. | .|. | 18 -0.066 0.008 128.87 0.000 .|. | .|. | 19 0.047 -0.032 129.80 0.000 .|. | .|. | 20 -0.045 -0.009 130.65 0.000 .|. | .|. | 21 0.016 0.035 130.76 0.000 .|. | *|. | 22 -0.009 -0.122 130.80 0.000 .|. | .|* | 23 0.062 0.094 132.40 0.000 *|. | **|. | 24 -0.074 -0.300 134.72 0.000 .|. | .|. | 25 0.057 -0.032 136.11 0.000 *|. | .|. | 26 -0.088 0.009 139.38 0.000 .|* | .|. | 27 0.082 -0.004 142.23 0.000 .|. | .|. | 28 -0.044 -0.056 143.06 0.000 .|. | .|. | 29 0.012 0.035 143.13 0.000 .|. | .|. | 30 0.024 0.063 143.37 0.000 .|. | .|. | 31 0.037 0.006 143.97 0.000 .|. | .|. | 32 -0.024 -0.022 144.23 0.000 .|. | .|. | 33 0.027 0.041 144.53 0.000 .|. | .|. | 34 0.035 -0.041 145.06 0.000 *|. | .|. | 35 -0.111 -0.065 150.46 0.000 .|. | **|. | 36 0.057 -0.210 151.89 0.000

备表2 AR（1，12）模型拟合序列D（S，1，12）

Dependent Variable: D(S,1,12)

Method: Least Squares

Date: 06/15/14 Time: 09:17

Sample (adjusted): 1950M02 1981M12

Included observations: 383 after adjustments

Convergence achieved after 2 iterations

Variable Coefficient Std. Error t-Statistic Prob.

AR(1) -0.105966 0.045015 -2.354026 0.0191

AR(12) -0.460293 0.045286 -10.16421 0.0000

R-squared 0.228345 Mean dependent var -0.253264 Adjusted R-squared 0.226320 S.D. dependent var 112.6660 S.E. of regression 99.10001 Akaike info criterion 12.03534 Sum squared resid 3741729. Schwarz criterion 12.05596 Log likelihood -2302.768 Hannan-Quinn criter. 12.04352 Durbin-Watson stat 2.030894

Inverted AR Roots .90-.24i .90+.24i .65-.66i .65+.66i

.23-.91i .23+.91i -.25+.90i -.25-.90i

-.67+.66i -.67-.66i -.91+.24i -.91-.24i

备表3 AR（1，12）模型拟合序列D（S，1，12）的残差分析

Date: 06/15/14 Time: 09:18

Sample: 1950M02 1981M12

Included observations: 383

Q-statistic probabilities

adjusted for 2 ARMAterm(s)

Autocorrelation Partial Correlation AC PAC Q-Stat Prob

.|. | .|. | 1 -0.018 -0.018 0.1232

.|* | .|* | 2 0.186 0.186 13.486

.|. | .|. | 3 0.024 0.031 13.707 0.000 .|* | .|. | 4 0.079 0.047 16.112 0.000 .|. | .|. | 5 0.020 0.013 16.269 0.001 .|. | .|. | 6 0.064 0.043 17.891 0.001 .|. | *|. | 7 -0.063 -0.073 19.472 0.002 .|. | .|. | 8 0.055 0.030 20.646 0.002 .|. | .|. | 9 0.018 0.040 20.770 0.004 *|. | *|. | 10 -0.105 -0.127 25.110 0.001 .|. | .|. | 11 0.070 0.064 27.077 0.001 *|. | *|. | 12 -0.165 -0.138 37.935 0.000 .|. | .|. | 13 -0.032 -0.055 38.339 0.000 .|. | .|. | 14 -0.024 0.030 38.570 0.000 .|. | .|. | 15 -0.061 -0.045 40.062 0.000 *|. | *|. | 16 -0.089 -0.066 43.262 0.000 .|. | .|. | 17 0.050 0.060 44.275 0.000 .|. | .|. | 18 -0.056 0.008 45.548 0.000 .|. | .|. | 19 0.043 0.015 46.280 0.000 .|. | .|. | 20 -0.056 -0.044 47.564 0.000 .|. | .|. | 21 0.034 0.058 48.041 0.000 .|. | *|. | 22 -0.054 -0.081 49.237 0.000 .|. | .|. | 23 0.024 0.014 49.464 0.000 **|. | **|. | 24 -0.326 -0.332 93.065 0.000 .|. | .|. | 25 0.053 0.021 94.201 0.000 *|. | .|. | 26 -0.132 -0.036 101.40 0.000 .|. | .|. | 27 -0.002 -0.010 101.40 0.000 *|. | .|. | 28 -0.080 -0.058 104.09 0.000 .|. | .|. | 29 0.005 0.045 104.10 0.000 .|. | .|* | 30 0.022 0.077 104.29 0.000 .|. | .|. | 31 0.012 -0.011 104.35 0.000 .|. | .|. | 32 -0.020 -0.014 104.52 0.000 .|. | .|. | 33 0.004 0.042 104.53 0.000 .|. | .|. | 34 0.068 -0.004 106.46 0.000 *|. | *|. | 35 -0.121 -0.097 112.64 0.000 .|. | *|. | 36 0.057 -0.107 114.02 0.000

备表4 MA（1，12）模型拟合序列D（S，1，12）

Dependent Variable: D(S,1,12)

Method: Least Squares

Date: 06/15/14 Time: 09:19

Sample (adjusted): 1949M02 1981M12

Included observations: 395 after adjustments

Convergence achieved after 8 iterations

MA Backcast: 1948M02 1949M01

Variable Coefficient Std. Error t-Statistic Prob.

MA(1) -0.090328 0.026833 -3.366290 0.0008

MA(12) -0.829737 0.026961 -30.77546 0.0000

R-squared 0.410415 Mean dependent var 0.496203 Adjusted R-squared 0.408915 S.D. dependent var 112.2025 S.E. of regression 86.26358 Akaike info criterion 11.75774 Sum squared resid 2924472. Schwarz criterion 11.77789 Log likelihood -2320.154 Hannan-Quinn criter. 11.76572 Durbin-Watson stat 2.074048

Inverted MA Roots .99 .86-.49i .86+.49i .50-.85i

.50+.85i .01-.98i .01+.98i -.48-.85i

-.48+.85i -.85-.49i -.85+.49i -.98

备表5 MA（1，12）模型拟合序列D（S，1，12）残差相关图

Date: 06/15/14 Time: 09:20

Sample: 1949M02 1981M12

Included observations: 395

Q-statistic probabilities

adjusted for 2 ARMA

term(s)

Autocorrelation Partial Correlation AC PAC Q-Stat Prob

.|. | .|. | 1 -0.038 -0.038 0.5651

.|* | .|* | 2 0.129 0.128 7.1929

.|. | .|. | 3 -0.042 -0.034 7.9031 0.005 .|. | .|. | 4 0.039 0.021 8.5218 0.014 .|. | .|. | 5 0.029 0.041 8.8563 0.031 .|. | .|. | 6 0.069 0.063 10.772 0.029 .|. | .|. | 7 -0.048 -0.052 11.692 0.039 .|. | .|. | 8 0.022 0.005 11.896 0.064 .|. | .|. | 9 -0.041 -0.026 12.582 0.083 *|. | *|. | 10 -0.089 -0.106 15.787 0.046 .|. | .|. | 11 0.028 0.030 16.105 0.065 .|. | .|. | 12 0.007 0.030 16.124 0.096 .|. | .|. | 13 0.040 0.034 16.767 0.115 .|. | .|. | 14 -0.035 -0.032 17.258 0.140 *|. | *|. | 15 -0.123 -0.126 23.550 0.036 *|. | *|. | 16 -0.071 -0.066 25.621 0.029 .|. | .|. | 17 0.050 0.063 26.655 0.032 .|. | .|. | 18 -0.018 -0.004 26.791 0.044 .|. | .|. | 19 0.022 0.002 27.002 0.058 .|. | .|. | 20 -0.044 -0.025 27.829 0.065 .|. | .|. | 21 -0.016 -0.005 27.940 0.085 .|. | .|. | 22 -0.023 -0.017 28.172 0.105 .|. | .|. | 23 0.027 0.024 28.469 0.127 .|. | .|. | 24 -0.044 -0.047 29.272 0.137 .|. | .|. | 25 0.050 0.010 30.318 0.140 *|. | *|. | 26 -0.087 -0.071 33.551 0.093 .|. | .|. | 27 -0.050 -0.052 34.615 0.095 .|. | .|. | 28 -0.061 -0.033 36.207 0.088 .|. | .|. | 29 0.010 0.011 36.252 0.110 .|. | .|. | 30 0.033 0.022 36.712 0.125 .|. | .|. | 31 -0.001 -0.021 36.713 0.154 .|. | .|. | 32 -0.033 -0.015 37.179 0.172 .|. | .|. | 33 -0.050 -0.041 38.265 0.173 .|. | .|. | 34 0.057 0.056 39.667 0.165 *|. | *|. | 35 -0.076 -0.076 42.196 0.131 .|. | .|. | 36 0.059 0.011 43.724 0.123

备表6ARMA（1，1）×（1，0，1）12拟合序列D(S，1，12)模型参数

Dependent Variable: D(S,1,12)

Method: Least Squares

Date: 06/15/14 Time: 09:22

Sample (adjusted): 1950M03 1981M12

Included observations: 382 after adjustments

Convergence achieved after 12 iterations

MA Backcast: 1949M02 1950M02

Variable Coefficient Std. Error t-Statistic Prob.

AR(1) -0.681190 0.190069 -3.583900 0.0004

SAR(12) 0.003097 0.062911 0.049231 0.9608

MA(1) 0.561335 0.215558 2.604099 0.0096

SMA(12) -0.824861 0.036153 -22.81585 0.0000

R-squared 0.421011 Mean dependent var -0.015707 Adjusted R-squared 0.416416 S.D. dependent var 112.7177 S.E. of regression 86.10805 Akaike info criterion 11.75950 Sum squared resid 2802717. Schwarz criterion 11.80081 Log likelihood -2242.064 Hannan-Quinn criter. 11.77589 Durbin-Watson stat 1.960860

Inverted AR Roots .62 .54-.31i .54+.31i .31+.54i

.31-.54i .00+.62i .00-.62i -.31-.54i

-.31+.54i -.54-.31i -.54+.31i -.62

-.68

Inverted MA Roots .98 .85+.49i .85-.49i .49-.85i

.49+.85i .00+.98i -.00-.98i -.49-.85i

-.49+.85i -.56 -.85+.49i -.85-.49i

-.98

备表7 ARMA（1，1）×（0，0，1）12拟合序列D(S，1，12)模型参数

Dependent Variable: D(S,1,12)

Method: Least Squares

Date: 06/15/14 Time: 09:24

Sample (adjusted): 1949M03 1981M12

Included observations: 394 after adjustments

Convergence achieved after 7 iterations

MA Backcast: 1948M02 1949M02

Variable Coefficient Std. Error t-Statistic Prob.

AR(1) -0.682895 0.179183 -3.811160 0.0002

MA(1) 0.565173 0.203393 2.778729 0.0057

SMA(12) -0.827297 0.029014 -28.51406 0.0000

R-squared 0.418267 Mean dependent var 0.812183 Adjusted R-squared 0.415291 S.D. dependent var 112.1691 S.E. of regression 85.77149 Akaike info criterion 11.74884 Sum squared resid 2876489. Schwarz criterion 11.77911 Log likelihood -2311.521 Hannan-Quinn criter. 11.76083 Durbin-Watson stat 1.958387

Inverted AR Roots -.68

Inverted MA Roots .98 .85-.49i .85+.49i .49+.85i

.49-.85i -.00-.98i -.00+.98i -.49-.85i

-.49+.85i -.57 -.85+.49i -.85-.49i

-.98

备表8 乘积模型的残差相关图

Date: 06/15/14 Time: 09:26

Sample: 1949M03 1981M12

Included observations: 394

Q-statistic probabilities adjusted for3 ARMA term(s)

Autocorrelation Partial Correlation AC PAC Q-Stat Prob

.|. | .|. | 1 0.019 0.019 0.1496

.|. | .|. | 2 0.044 0.043 0.9103

.|. | .|. | 3 0.015 0.013 1.0002

.|. | .|. | 4 -0.002 -0.005 1.0022 0.317 .|. | .|. | 5 0.070 0.069 2.9646 0.227 .|. | .|. | 6 0.057 0.055 4.2706 0.234 .|. | .|. | 7 -0.028 -0.036 4.5878 0.332 .|. | .|. | 8 0.016 0.010 4.6904 0.455 .|. | .|. | 9 -0.038 -0.036 5.2608 0.511 *|. | *|. | 10 -0.099 -0.104 9.2814 0.233 .|. | .|. | 11 0.044 0.043 10.081 0.259 .|. | .|. | 12 0.009 0.020 10.117 0.341 .|. | .|. | 13 -0.014 -0.015 10.192 0.424 .|. | .|. | 14 -0.041 -0.041 10.883 0.453 *|. | *|. | 15 -0.145 -0.126 19.501 0.077 .|. | .|. | 16 -0.061 -0.053 21.026 0.072 .|. | .|. | 17 0.061 0.066 22.544 0.068 .|. | .|. | 18 -0.012 0.000 22.600 0.093 .|. | .|. | 19 0.021 0.016 22.777 0.120 .|. | .|. | 20 -0.034 -0.022 23.261 0.141 .|. | .|. | 21 -0.036 -0.010 23.811 0.161 .|. | .|. | 22 -0.009 -0.016 23.841 0.202 .|. | .|. | 23 0.032 0.026 24.264 0.231 .|. | .|. | 24 -0.038 -0.051 24.883 0.252 .|. | .|. | 25 -0.002 -0.032 24.884 0.303 *|. | *|. | 26 -0.097 -0.085 28.871 0.185 *|. | .|. | 27 -0.066 -0.043 30.701 0.163 .|. | .|. | 28 -0.038 -0.041 31.324 0.179 .|. | .|. | 29 0.024 0.026 31.564 0.208 .|. | .|. | 30 0.037 0.022 32.143 0.227 .|. | .|. | 31 0.007 0.001 32.162 0.268 .|. | .|. | 32 -0.042 -0.017 32.933 0.280 .|. | .|. | 33 -0.045 -0.032 33.798 0.289 .|. | .|. | 34 0.044 0.037 34.656 0.298 .|. | *|. | 35 -0.049 -0.066 35.689 0.299 .|. | .|. | 36 0.039 0.008 36.363 0.315

多元时间序列建模分析

应用时间序列分析实验报告

单位根检验输出结果如下：序列x的单位根检验结果：

1967 58.8 53.4 1968 57.6 50.9 1969 59.8 47.2 1970 56.8 56.1 1971 68.5 52.4 1972 82.9 64.0 1973 116.9 103.6 1974 139.4 152.8 1975 143.0 147.4 1976 134.8 129.3 1977 139.7 132.8 1978 167.6 187.4 1979 211.7 242.9 1980 271.2 298.8 1981 367.6 367.7 1982 413.8 357.5 1983 438.3 421.8 1984 580.5 620.5 1985 808.9 1257.8 1986 1082.1 1498.3 1987 1470.0 1614.2 1988 1766.7 2055.1 1989 1956.0 2199.9 1990 2985.8 2574.3 1991 3827.1 3398.7 1992 4676.3 4443.3 1993 5284.8 5986.2 1994 10421.8 9960.1 1995 12451.8 11048.1 1996 12576.4 11557.4 1997 15160.7 11806.5 1998 15223.6 11626.1 1999 16159.8 13736.5 2000 20634.4 18638.8 2001 22024.4 20159.2 2002 26947.9 24430.3 2003 36287.9 34195.6 2004 49103.3 46435.8 2005 62648.1 54273.7 2006 77594.6 63376.9 2007 93455.6 73284.6 2008 100394.9 79526.5 run; proc gplot; plot x*t=1 y*t=2/overlay; symbol1c=black i=join v=none; symbol2c=red i=join v=none w=2l=2; run; proc arima data=example6_4; identify var=x stationarity=(adf=1); identify var=y stationarity=(adf=1); run; proc arima; identify var=y crrosscorr=x; estimate methed=ml input=x plot; forecast lead=0id=t out=out; proc aima data=out; identify varresidual stationarity=(adf=2); run;

统计基础知识第五章时间序列分析习题及答案

第五章时间序列分析 一、单项选择题 1.构成时间数列的两个基本要素是( C )（2012年1月） A.主词和宾词 B.变量和次数 C.现象所属的时间及其统计指标数值 D.时间和次数 2．某地区历年出生人口数是一个( B )（2011年10月） A．时期数列 B.时点数列 C.分配数列 D.平均数数列 3.某商场销售洗衣机，2008年共销售6000台，年底库存50台，这两个指标是( C ) （2010年10） A.时期指标 B.时点指标 C.前者是时期指标，后者是时点指标 D.前者是时点指标，后者是时期指标 4.累计增长量( A ) （2010年10） A.等于逐期增长量之和 B.等于逐期增长量之积 C.等于逐期增长量之差 D.与逐期增长量没有关系 5.某企业银行存款余额4月初为80万元，5月初为150万元，6月初为210万元，7月初为160万元，则该企业第二季度的平均存款余额为（ C ）（2009年10） 万元万元万元万元 6.下列指标中属于时点指标的是( A ) （2009年10） A.商品库存量 B.商品销售量 C.平均每人销售额 D.商品销售额 7.时间数列中，各项指标数值可以相加的是( A ) （2009年10） A.时期数列 B.相对数时间数列 C.平均数时间数列 D.时点数列 8.时期数列中各项指标数值（ A ）（2009年1月） A.可以相加 B.不可以相加 C.绝大部分可以相加 D.绝大部分不可以相加 10.某校学生人数2005年比2004年增长了8%，2006年比2005年增长了15%，2007年比2006年增长了18%，则2004-2007年学生人数共增长了（ D ）（2008年10月） ％+15％+18％％×15％×18％ C.（108％+115％+118％）-1 ％×115％×118％-1 二、多项选择题 1.将不同时期的发展水平加以平均而得到的平均数称为( ABD )（2012年1月） A.序时平均数 B.动态平均数 C.静态平均数 D.平均发展水平 E.一般平均数2．定基发展速度和环比发展速度的关系是( BD )（2011年10月） A．相邻两个环比发展速度之商等于相应的定基发展速度 B.环比发展速度的连乘积等于定基发展速度

时间序列分析实验报告

时间序列分析实验报告 P185#1、某股票连续若干天的收盘价如表5-4 （行数据）所示。 表5-4 304 303 307 299 296 293301 293 301 295 284286 286 287 284 282278 281 278 277279 278 270 268 272 273 279 279280 275 271 277 278279 283 284 282 283279 280 280 279278 283 278 270 275 273 273 272275 273 273 272 273272 273 271 272 271273 277 274 274272 280 282 292 295 295 294 290 291 288 288 290 293 288 289 291 293 293 290 288 287 289 292 288 288 285 282 286 286 287 284 283 286 282 287 286 287 292 292 294 291 288 289 选择适当模型拟合该序列的发展，并估计下一天的收盘价。 解： （1）通过SA漱件画出上述序列的时序图如下： 程序： data example5_1; in put x@@; time=_ n_; cards ; 304 303 307 299296 293 301 293 301 295 284286286 287 284 282 278 281 278277 279 278 270 268 272 273279279 280 275 271 277 278 279283 284 282 283 279 280 280279278 283 278 270 275 273 273272 275 273 273 272 273 272273271 272 271 273 277 274 274272 280 282 292 295 295 294290291 288 288 290 293 288 289291 293 293 290 288 287 289292288 288 285 282 286 286 287284 283 286 282 287 286 287292292 294 291 288 289 proc gplot data =example5_1; plot x*time= 1; symbol1 c=black v=star i =join; run ; 上述程序所得时序图如下： 上述时序图显示，该序列具有长期趋势又含有一定的周期性，为典型的非平稳序列。又因为该序列呈现曲线形式，所以选择2阶差分。

时间序列分析_最经典的

【时间简“识”】 说明：本文摘自于经管之家(原人大经济论坛) 作者：胖胖小龟宝。原版请到经管之家(原人大经济论坛) 查看。 1.带你看看时间序列的简史 现在前面的话—— 时间序列作为一门统计学，经济学相结合的学科，在我们论坛，特别是五区计量经济学中是热门讨论话题。本月楼主推出新的系列专题——时间简“识”，旨在对时间序列方面进行知识扫盲（扫盲，仅仅扫盲而已……），同时也想借此吸引一些专业人士能够协助讨论和帮助大家解疑答惑。 在统计学的必修课里，时间序列估计是遭吐槽的重点科目了，其理论性强，虽然应用领域十分广泛，但往往在实际操作中会遇到很多“令人发指”的问题。所以本帖就从基础开始，为大家絮叨絮叨那些关于“时间”的故事！

Long long ago，有多long？估计大概7000年前吧，古埃及人把尼罗河涨落的情况逐天记录下来，这一记录也就被我们称作所谓的时间序列。记录这个河流涨落有什么意义？当时的人们并不是随手一记，而是对这个时间序列进行了长期的观察。结果，他们发现尼罗河的涨落非常有规律。掌握了尼罗河泛滥的规律，这帮助了古埃及对农耕和居所有了规划，使农业迅速发展，从而创建了埃及灿烂的史前文明。 好~~从上面那个故事我们看到了 1、时间序列的定义——按照时间的顺序把随机事件变化发展的过程记录下来就构成了一个时间序列。 2、时间序列分析的定义——对时间序列进行观察、研究，找寻它变化发展的规律，预测它将来的走势就是时间序列分析。 既然有了序列，那怎么拿来分析呢？ 时间序列分析方法分为描述性时序分析和统计时序分析。 1、描述性时序分析——通过直观的数据比较或绘图观测，寻找序列中蕴含的发展规律，这种分析方法就称为描述性时序分析 ?描述性时序分析方法具有操作简单、直观有效的特点，它通常是人们进行统计时序分析的第一步。

时间序列分析实验报告汇总.doc

《时间序列分析》课程实验报告

一、上机练习（P124） 1.拟合线性趋势 12.79 14.02 12.92 18.27 21.22 18.81 25.73 26.27 26.75 28.73 31.71 33.95 程序： data xiti1; input x@@; t=_n_; cards; 12.79 14.02 12.92 18.27 21.22 18.81 25.73 26.27 26.75 28.73 31.71 33.95 ; proc gplot data=xiti1; plot x*t; symbol c=red v=star i=join; run; proc autoreg data=xiti1; model x=t; output predicted=xhat out=out; run; proc gplot data=out; plot x*t=1 xhat*t=2/overlay; symbol2c=green v=star i=join; run; 运行结果：

分析：上图为该序列的时序图，可以看出其具有明显的线性递增趋势，故使用线性模型进行拟合：x t=a+bt+I t,t=1,2,3,…,12 分析：上图为拟合模型的参数估计值，其中a=9.7086,b=1.9829，它们的检验P值均小于 0.0001，即小于显著性水平0.05，拒绝原假设，故其参数均显著。从而所拟合模型为： x t=9.7086+1.9829t.

分析：上图中绿色的线段为线性趋势拟合线，可以看出其与原数据基本吻合。 2.拟合非线性趋势 1.85 7.48 14.29 23.02 37.42 74.27 140.72 265.81 528.23 1040.27 2064.25 4113.73 8212.21 16405.95 程序： data xiti2; input x@@; t=_n_; cards; 1.85 7.48 14.29 23.02 37.42 74.27 140.72 265.81 528.23 1040.27 2064.25 4113.73 8212.21 16405.95 ; proc gplot data=xiti2; plot x*t; symbol c=red v=star i=none; run; proc nlin method=gauss; model x=a*b**t; parameters a=0.1 b=1.1; der.a=b**t; der.b=a*t*b**(t-1); output predicted=xh out=out; run; proc gplot data=out; plot x*t=1 xh*t=2/overlay;

spss时间序列模型

《统计软件实验报告》SPSS软件的上机实践应用 时间序列分析

数学与统计学学院 一、实验内容： 时间序列是指一个依时间顺序做成的观察资料的集合。时间序列分析过程中最常用的方法是：指数平滑、自回归、综合移动平均及季节分解。 本次实验研究就业理论中的就业人口总量问题。但人口经济的理论和实践表明，就业总量往往受到许多因素的制约，这些因素之间有着错综复杂的联系，因此，运用结构性的因果模型分析和预测就业总量往往是比较困难的。时间序列分析中的自回归求积分移动平均法（ARIMA）则是一个较好的选择。对于时间序列的短期预测来说，随机时序ARIMA是一种精度较高的模型。 我们已辽宁省历年（1969-2005）从业人员人数为数据基础建立一个就业总量的预测时间序列模型,通过spss建立模型并用此模型来预测就业总量的未来发展趋势。 二、实验目的： 1.准确理解时间序列分析的方法原理 2.学会实用SPSS建立时间序列变量 3.学会使用SPSS绘制时间序列图以反应时间序列的直观特征。

4.掌握时间序列模型的平稳化方法。 5.掌握时间序列模型的定阶方法。 6.学会使用SPSS建立时间序列模型与短期预测。 7.培养运用时间序列分析方法解决身边实际问题的能力。 三、实验分析： 总体分析： 先对数据进行必要的预处理和观察，直到它变成稳态后再用SPSS对数据进行分析。 数据的预处理阶段，将它分为三个步骤：首先，对有缺失值的数据进行修补，其次将数据资料定义为相应的时间序列，最后对时间序列数据的平稳性进行计算观察。 数据分析和建模阶段：根据时间序列的特征和分析的要求，选择恰当的模型进行数据建模和分析。 四、实验步骤： SPSS的数据准备包括数据文件的建立、时间定义和数据期间的指定。 SPSS的时间定义功能用来将数据编辑窗口中的一个或多个变量指定为时间序列变量，并给它们赋予相应的时间标志，具体操作步骤是： 1.选择菜单：Date→Define Dates，出现窗口：

第五章 时间序列的模型识别

第五章时间序列的模型识别 前面四章我们讨论了时间序列的平稳性问题、可逆性问题，关于线性平稳时间序列模型，引入了自相关系数和偏自相关系数，由此得到ARMA(p, q)统计特性。从本章开始，我们将运用数据开始进行时间序列的建模工作，其工作流程如下： 图5.1 建立时间序列模型流程图 在ARMA(p,q)的建模过程中，对于阶数(p,q)的确定，是建模中比较重要的步骤，也是比较困难的。需要说明的是，模型的识别和估计过程必然会交叉，所以，我们可以先估计一个比我们希望找到的阶数更高的模型，然后决定哪些方面可能被简化。在这里我们使用估计过程去完成一部分模型识别，但是这样得到的模型识别必然是不精确的，而且在模型识别阶段对于有关问题没有精确的公式可以利用，初步识别可以我们提供有关模型类型的试探性的考虑。 对于线性平稳时间序列模型来说，模型的识别问题就是确定ARMA(p,q)过程的阶数，从而判定模型的具体类别，为我们下一步进行模型的参数估计做准备。所采用的基本方法主要是依据样本的自相关系数（ACF）和偏自相关系数（PACF）初步判定其阶数，如果利用这种方法无法明确判定模型的类别，就需要借助诸如AIC、BIC 等信息准则。我们分别给出几种定阶方法，它们分别是（1）利用时间序列的相关特性，这是识别模型的基本理论依据。如果样本的自相关系数（ACF）在滞后q+1阶时突然截断，即在q处截尾，那么我们可以判定该序列为MA(q)序列。同样的道理，如果样本的偏自相关系数（PACF）在p处截尾，那么我们可以判定该序列为AR(p)序列。如果ACF和PACF 都不截尾，只是按指数衰减为零，则应判定该序列为ARMA(p,q)序列，此时阶次尚需作进一步的判断；（2）利用数理统计方法检验高阶模型新增加的参数是否近似为零，根据模型参数的置信区间是否含零来确定模型阶次，检验模型残差的相关特性等；（3）利用信息准则，确定一个与模型阶数有关

应用时间序列分析 第5章

佛山科学技术学院 应用时间序列分析实验报告 实验名称第五章非平稳序列的随机分析 一、上机练习 通过第4章我们学习了非平稳序列的确定性因素分解方法，但随着研究方法的深入和研究领域的拓宽，我们发现确定性因素分解方法不能很充分的提取确定性信息以及无法提供明确有效的方法判断各因素之间确切的作用关系。第5章所介绍的随机性分析方法弥补了确定性因素分解方法的不足，为我们提供了更加丰富、更加精确的时序分析工具。 5.8.1 拟合ARIMA模型 【程序】 data example5_1; input x@@; difx=dif(x); t=_n_; cards; 1.05 -0.84 -1.42 0.20 2.81 6.72 5.40 4.38 5.52 4.46 2.89 -0.43 -4.86 -8.54 -11.54 -1 6.22 -19.41 -21.61 -22.51 -23.51 -24.49 -25.54 -24.06 -23.44 -23.41 -24.17 -21.58 -19.00 -14.14 -12.69 -9.48 -10.29 -9.88 -8.33 -4.67 -2.97 -2.91 -1.86 -1.91 -0.80 ; proc gplot; plot x*t difx*t; symbol v=star c=black i=join; proc arima; identify var=x(1); estimate p=1; estimate p=1 noint; forecast lead=5id=t out=out; proc gplot data=out; plot x*t=1 forecast*t=2 l95*t=3 u95*t=3/overlay; symbol1c=black i=none v=star; symbol2c=red i=join v=none; symbol3c=green I=join v=none;

时间序列分析实验报告

时间序列分析SAS软件实验报告： 以我国2002第一季度到2012年第一季度国内生产总值数据（季节效应模型）分析 班级：统计系统计0姓名： 学号： 指导老师： 20 年月日

时间序列分析报告 一、前言 【摘要】2012年3月5日温家宝代表国务院向大会作政府工作报告。温家宝在报告中提出，2012年国内生产总值增长7.5%。这是我国国内生产总值（GDP）预期增长目标八年来首次低于8%。 温家宝说，今年经济社会发展的主要预期目标是：国内生产总值增长7.5%；城镇新增就业900万人以上，城镇登记失业率控制在4.6%以内；居民消费价格涨幅控制在4%左右；进出口总额增长10%左右，国际收支状况继续改善。同时，要在产业结构调整、自主创新、节能减排等方面取得新进展，城乡居民收入实际增长和经济增长保持同步。 他指出，这里要着重说明，国内生产总值增长目标略微调低，主要是要与“十二五”规划目标逐步衔接，引导各方面把工作着力点放到加快转变经济发展方式、切实提高经济发展质量和效益上来，以利于实现更长时期、更高水平、更好质量发展。提出居民消费价格涨幅控制在4%左右，综合考虑了输入性通胀因素、要素成本上升影响以及居民承受能力，也为价格改革预留一定空间。 对于这一预期目标的调整，温家宝解释说，主要是要与“十二五”规划目标逐步衔接，引导各方面把工作着力点放到加快转变经济发展方式、切实提高经济发展质量和效益上来，以利于实现更长时期、更高水平、更好质量发展。 央行货币政策委员会委员李稻葵表示，未来若干年中国经济增长速度会有所放缓，这个放缓是必要的，是经济发展方式转变的一个必然要求。 【关键词】“十二五”规划目标国内生产总值增长率增速放缓提高发展质量附表：国内生产总值(2012年1季度) 绝对额（亿元）比去年同期增长（%） 国内生产总值107995.0 8.1 第一产业6922.0 3.8 第二产业51450.5 9.1 第三产业49622.5 7.5 注1：绝对额按现价计算，增长速度按不变价计算。注2：该表为初步核算数据。 GDP环比增长速度 环比增长速度（%） 2011年1季度 2.2 2季度 2.3 3季度 2.4 4季度 1.9 2012年1季度 1.8 注：环比增长速度为经季节调整与上一季度对比的增长速度。 此表是我国2012年第一季度国内生产总值及与2011年同期比较来源：前瞻网

时间序列分析第三章平稳时间序列分析

应用时间序列分析实验报告 实验名称第三章平稳时间序列分析 一、上机练习 data example3_1; input x; time=_n_; cards; 0.30 -0.45 0.036 0.00 0.17 0.45 2.15 4.42 3.48 2.99 1.74 2.40 0.11 0.96 0.21 -0.10 -1.27 -1.45 -1.19 -1.47 -1.34 -1.02 -0.27 0.14 -0.07 0.10 -0.15 -0.36 -0.50 -1.93 -1.49 -2.35 -2.28 -0.39 -0.52 -2.24 -3.46 -3.97 -4.60 -3.09 -2.19 -1.21 0.78 0.88 2.07 1.44 1.50 0.29 -0.36 -0.97 -0.30 -0.28 0.80 0.91 1.95 1.77 1.80 0.56 -0.11 0.10 -0.56 -1.34 - 2.47 0.07 -0.69 -1.96 0.04 1.59 0.20 0.39 1.06 -0.39 -0.16 2.07 1.35 1.46 1.50 0.94 -0.08 -0.66 -0.21 -0.77 -0.52 0.05 ; procgplot data=example3_1; plot x*time=1; symbolc=red i=join v=star; run; 建立该数据集，绘制该序列时序图得： 根据所得图像，对序列进行平稳性检验。时序图就是一个平面二维坐标图，通常横轴表示时间，纵

轴表示序列取值。时序图可以直观地帮助我们掌握时间序列的一些基本分布特征。 根据平稳时间序列均值、方差为常数的性质，平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动，而且波动的X围有界的特点。如果观察序列的时序图，显示出该序列有明显的趋势性或周期性，那它通常不是平稳序列。从图上可以看出，数值围绕在0附近随机波动，没有明显或周期，其本可以视为平稳序列，时序图显示该序列波动平稳。 procarima data=example3_1; identifyvar=x nlag=8; run; 图一 图二样本自相关图 图三样本逆自相关图

应用时间序列实验报告

河南工程学院课程设计《时间序列分析课程设计》学生姓名学号： 学院：理学院 专业班级： 专业课程：时间序列分析课程设计 指导教师： 2017年6月2日

目录 1. 实验一澳大利亚常住人口变动分析 (1) 1.1 实验目的 (1) 1.2 实验原理 (1) 1.3 实验内容 (2) 1.4 实验过程 (3) 2. 实验二我国铁路货运量分析 (8) 2.1 实验目的 (8) 2.2 实验原理 (8) 2.3 实验内容 (9) 2.4 实验过程 (10) 3. 实验三美国月度事故死亡数据分析 (14) 3.1 实验目的 (14) 3.2 实验原理 (15) 3.3 实验内容 (15) 3.4 实验过程 (16) 课程设计体会 (19)

1.实验一澳大利亚常住人口变动分析 1971年9月—1993年6月澳大利亚常住人口变动（单位：千人）情况如表1-1所示（行数据）。 表1-1 （1）判断该序列的平稳性与纯随机性。 （2）选择适当模型拟合该序列的发展。 （3）绘制该序列拟合及未来5年预测序列图。 1.1 实验目的 掌握用SAS软件对数据进行相关性分析，判断序列的平稳性与纯随机性,选择模型拟合序列发展。 1.2 实验原理 （1）平稳性检验与纯随机性检验 对序列的平稳性检验有两种方法，一种是根据时序图和自相关图显示的特征做出判断的图检验法；另一种是单位根检验法。

（2）模型识别 先对模型进行定阶，选出相对最优的模型，下一步就是要估计模型中未知参数的值，以确定模型的口径，并对拟合好的模型进行显著性诊断。 （3）模型预测 模型拟合好之后，利用该模型对序列进行短期预测。 1.3 实验内容 （1）判断该序列的平稳性与纯随机性 时序图检验，根据平稳时间序列均值、方差为常数的性质，平稳序列的时序图应该显示出该序列始终在一个常识值附近波动，而且波动的范围有界。如果序列的时序图显示该序列有明显的趋势性或周期性，那么它通常不是平稳序列。 对自相关图进行检验时，可以用SAS 系统ARIMA 过程中的IDENTIFY 语句来做自相关图。 而单位根检验我们用到的是DF 检验。以1阶自回归序列为例： 11t t t x x φε-=+ 该序列的特征方程为： 0λφ-= 特征根为： λφ= 当特征根在单位圆内时： 11φ< 该序列平稳。 当特征根在单位圆上或单位圆外时： 11φ≥ 该序列非平稳。 对于纯随机性检验，既白噪声检验，可以用SAS 系统中的IDENTIFY 语句来输出白噪声检验的结果。 （2）选择适当模型拟合该序列的发展

平稳时间序列预测法

7 平稳时间序列预测法 7.1 概述 7.2 时间序列的自相关分析 7.3 单位根检验和协整检验 7.4 ARMA模型的建模 回总目录 7.1 概述 时间序列取自某一个随机过程，则称： 一、平稳时间序列 过程是平稳的――随机过程的随机特征不随时间变化而变化过程是非平稳的――随机过程的随机特征随时间变化而变化回总目录 回本章目录 宽平稳时间序列的定义： 设时间序列 ，对于任意的t,k和m，满足： 则称宽平稳。 回总目录

回本章目录 Box-Jenkins方法是一种理论较为完善的统计预测方法。 他们的工作为实际工作者提供了对时间序列进行分析、预测，以及对ARMA模型识别、估计和诊断的系统方 法。使ARMA模型的建立有了一套完整、正规、结构 化的建模方法，并且具有统计上的完善性和牢固的理 论基础。 ARMA模型是描述平稳随机序列的最常用的一种模型； 回总目录 回本章目录 ARMA模型三种基本形式： 自回归模型（AR：Auto-regressive）； 移动平均模型（MA：Moving-Average）； 混合模型（ARMA：Auto-regressive Moving-Average）。回总目录 回本章目录 如果时间序列满足 其中是独立同分布的随机变量序列,且满足：

则称时间序列服从p阶自回归模型。 二、自回归模型 回总目录 回本章目录 自回归模型的平稳条件： 滞后算子多项式 的根均在单位圆外，即 的根大于1。 回总目录 回本章目录 如果时间序列满足 则称时间序列服从q阶移动平均模型。或者记为。 平稳条件：任何条件下都平稳。

三、移动平均模型MA(q) 回总目录 回本章目录 四、ARMA(p,q)模型 如果时间序列 满足： 则称时间序列服从(p,q)阶自回归移动平均模型。 或者记为： 回总目录 回本章目录 q=0，模型即为AR(p)； p=0，模型即为MA(q)。 ARMA(p,q)模型特殊情况： 回总目录 回本章目录 例题分析 设 ，其中A与B 为两个独立的零均值随机变量，方差为1；

时间序列分析第五章作业

时间序列分析第五章作业 班级：09数学与应用数学 学号： 姓名： 习题5.7 1、 根据数据，做出它的时序图及一阶差分后图形，再用ARIMA 模型模拟该序列的发展，得出 预测。根据输出的结果，我们知道此为白噪声，为非平稳序列，同时可以得出序列t x 模型 应该用随机游走模型(0，1，0)模型来模拟，模型为：，并可以预测到下一天 的收盘价为296.0898。 各代码： data example5_1; input x@@; difx=dif(x); t=_n_; cards ; 304 303 307 299 296 293 301 293 301 295 284 286 286 287 284 282 278 281 278 277 279 278 270 268 272 273 279 279 280 275 271 277 278 279 283 284 282 283 279 280 280 279 278 283 278 270 275 273 273 272 275 273 273 272 273 272 273 271 272 271 273 277 274 274 272 280 282 292 295 295 294 290 291 288 288 290 293 288 289 291 293 293 290 288 287 289 292 288 288 285 282 286 286 287 284 283 286 282 287 286 287 292 292 294 291 288 289 ; proc gplot ; plot x*t difx*t; symbol v =star c =black i =join; proc arima data =example5_1; identify Var =x(1) nlag =8 minic p = (0:5) q = (0:5); estimate p =0 q =0 noint; forecast lead =1 id =t out =results; run ; proc gplot data =results; plot x*t=1 forecast*t=2 l95*t=3 u95*t=3/overlay ; symbol1 c =black i =none v =star; symbol2 c =red i =join v =none; symbol3 c =green i =join v =none l =32; run ; 时序图：

时间序列 实验报告

数学与软件科学学院实验报告 学期：2013至 2014 第 2 学期 2014年4月24日课程名称: 应用时间序列分析专业:统计学 2011级6班实验编号： 01 实验项目：平稳时间序列分析指导教师：XXX 姓名： XX 学号：XXXX 实验成绩：＿＿＿＿＿ 实验步骤 选择合适的模型拟合1950年－2008年我国邮路及农村投递线路每年新增里程数序列。 首先绘制该序列时序图，直观检验序列的平稳性： 时序图显示：序列具有平稳特征。 接着进行白噪声检验：使用Q统计量，如下： 显示序列值彼此之间蕴含着相关关系，为非白噪声序列。该序列为平稳的非白噪声序列，可以建立一个平稳的模型来拟合；

考察序列自相关图以及偏自相关图 样本自相关图显示除了延迟1-3阶的自相关系数在2倍标准差范围之外，其他阶数的自相关系数都在2倍标准差范围内波动。根据自相关系数的这个特点可以判断该序列具有短期相关性，进一步确定序列平稳。 考察自相关系数衰减向零的过程，可以看到有明显的正弦波动轨迹，这说明自相关系数具有拖尾的典型特征 考察偏自相关系数衰减向零的过程，除了1-2阶偏自相关系数在2倍标准差范围之外，其他阶数的自相关系数都在2倍标准差范围内做小值无序波动，这是一个典型的偏相关系数2阶截尾特征 本例中，根据自相关系数拖尾，偏自相关系数2阶截尾属性，我们可以初步确定拟合模型为AR(2)模型。 进行参数估计，结果如下： Coefficient Std. Error t-Statistic Prob. C 10.83741 3.234053 3.351029 0.0015 AR(1) 0.728590 0.113885 6.397592 0.0000 AR(2) -0.544583 0.114077 -4.773838 0.0000 R-squared 0.453915 Mean dependent var 10.95316 Adjusted R-squared 0.433689 S.D. dependent var 26.47445 S.E. of regression 19.92298 Akaike info criterion 8.872821 Sum squared resid 21433.96 Schwarz criterion 8.980350 Log likelihood -249.8754 Hannan-Quinn criter. 8.914610 F-statistic 22.44281 Durbin-Watson stat 2.104218 Prob(F-statistic) 0.000000 Inverted AR Roots .36+.64i .36-.64i

时间序列分析实验报告70946

时间序列分析实验报告 Ｐ185＃1、某股票连续若干天的收盘价如表5—4(行数据）所示。 表5－4 ３04 303 307 299 296 293 ３0１293 301 ２95 284 286 2８6 ２87 2８4 ２82 278 28１２78 277 279 278 270 ２68 ２72 ２73 ２79 2７9 280 27５２７1 277 ２７8 27９ 28３２84 282 ２８3 2７9 280 ２80 27９ 278 2８３２7８27０ 275 273 273 2７2 2７5 27３２7３２72 2７3 27２２7３ 271 ２7２ 271 ２73 ２77 274 2７4 27２２80 2８2 29２ 29５ 29５ 294 ２90 291 288 ２88 ２9０ 2９3 ２８８ 289 2９1 ２93 2９3 29０288 2８７ 289 ２92 ２８8 2８8 285 282 286 ２８6 ２87 ２8４ 2８3 28６ 28２ 28７ 2８6 2８7 292 29２ 294 291 28８ 2８９ 选择适当模型拟合该序列的发展，并估计下一天的收盘价。 解: （１）通过ＳＡＳ软件画出上述序列的时序图如下： 程序: ｄａta eｘａmｐle5＿1； inpuｔ x@＠； time＝_ｎ＿; ｃａrｄs; 304 303 30７299 2９６２93 ３01 2９3 3０1 295 284 2８6 286 287 284 28２ 278 28１2７8 ２77 ２79 2７８ 27０268 ２７２ 27３２79 279 ２8０275 ２71 277 278 2７９ 283 28４ 282 283 279 ２80 280 ２79 ２78 28３ 278 270 2７5 ２7３２73 ２７2 2７5 273 2７3 272 2７3 272 27３ 27１２72 27１ 2７3 ２77 27４２74 ２72 28０ 2８2 29２２9５ 295 2９4 290 29１２8８ 288 ２90 29３288 289 291 29３ 2９3 290 2８８ 287 289 292 288 288 285 282 2８6 ２86 28７ 2８４２83 286 282 2８7 286 287 ２92 2９2 2９４ 291 288 ２8９ ; pｒｏc gplot datａ=examplｅ5_1; ploｔx*ｔiｍe＝1； symbol１c=ｂlacｋｖ=ｓｔａr i=ｊoiｎ; run； 上述程序所得时序图如下：

时间序列分析基于R——习题答案

第一章习题答案 略 第二章习题答案 （1）非平稳 （2） （3）典型的具有单调趋势的时间序列样本自相关图 （1）非平稳，时序图如下 （2）-（3）样本自相关系数及自相关图如下：典型的同时具有周期和趋势序列的样本自相关图

（1）自相关系数为： （2）平稳序列 （3）白噪声序列 ，序列不能视为纯随机序列。LB=，LB统计量对应的分位点为，P值为。显著性水平=0.05 （1）时序图与样本自相关图如下 （2）非平稳 （3）非纯随机

（1）平稳，非纯随机序列（拟合模型参考：ARMA(1,2)） （2）差分序列平稳，非纯随机 第三章习题答案 ()0t E x =,2 1 () 1.9610.7 t Var x ==-,220.70.49ρ==,220φ= 1715φ=,2115 φ= ()0t E x =,10.15 () 1.98(10.15)(10.80.15)(10.80.15) t Var x += =--+++ 10.8 0.7010.15 ρ= =+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-= 1110.70φρ==,2220.15φφ==-,330φ= 10c -<<, 1121,1,2 k k k c c k ρρρρ--?=? -??=+≥? 证明: 该序列的特征方程为：32--c 0c λλλ+=，解该特征方程得三个特征根： 11λ= ，2λ= 3λ= 无论c 取什么值，该方程都有一个特征根在单位圆上，所以该序列一定是非平稳序列。证毕。 (1)错 （2）错 （3）对 （4）错 （5） 该模型有两种可能的表达式：11 2 t t t x εε-=-和12t t t x εε-=-。 将123100.50.8t t t t t x x C εεε---=++-+等价表达为 ()23 23223310.82010.510.8(10.50.50.5)t t t B CB x B B CB B B B εε-+-=-=-+++++ 展开等号右边的多项式，整理为

时间序列分析第五章上机指导

上机指导 第五章 拟合ARIMA模型 由于ARMA模型是ARIMA模型的一种特例，所以在SAS系统中这两种模型的拟合都放在了ARIMA过程中。我们已经在第3章进行了ARMA模型拟合时介绍了ARIMA过程的基本命令格式。再次以临时数据集example5_1的数据为例介绍ARIMA模型拟合与ARMA模型拟合的不同之处。 data example5_1; input x@@; difx=dif(x); t=_n_; cards; proc gplot; plot x*t difx*t; symbol v=star c=black i=join; run; 输出时序图显示这是一个典型的非平稳序列。如图5-49所示

图5-49 序列x时序图 考虑对该序列进行1阶差分运算，同时考察查分后序列的平稳性，在原程序基础上添加相关命令，程序修改如下： data example5_1; input x@@; difx=dif(x); t=_n_; cards; proc gplot; plot x*t difx*t; symbol v=star c=black i=join; proc arima; identify var=x(1);

estimate p=1; forecast lead=5 id=t ; run; 语句说明： （1）DATA步中的命令“difx=dif(x);”,这是指令系统对变量x进行1阶差分，差分后的序列值赋值给变量difx。其中dif（）是差分函数，假如要差分的变量名为x，常见的几种差分表示为： 1阶差分：dif（x） 2阶差分：dif（dif（x）） k步差分：difk（x） （2）我们在GPLOT过程中添加绘制了一个时序图“difx*t”，这是为了直观考察1阶差分后序列的平稳性。所得时序图如图5-50所示。 图5-50 序列difx时序图 时序图显示差分后序列difx没有明显的非平稳特征。 （3）“identify var=x（1）；”，使用该命令可以识别查分后序列的平稳性、纯随机性和适当的拟合模型阶数。其中x（1）表示识别变量x的1阶差分后序列。SAS支持多种形式的差分序列识别： var=x（1），表示识别变量x的1阶查分后序列Δxt；

时间序列分析实验报告

H a r b i n I n s t i t u t e o f T e c h n o l o g y 实验报告 课程名称：时间序列分析 设计题目：非平稳时间序列建模 院系：电信学院 班级： 设计者： 学号： 指导教师：冀振元 设计时间： 2010-05-07

一、绪论 稳序列的直观含义就是序列中不存在任何趋势性和周期性,其统计意义就是一阶矩为常数，二阶矩存在且为时间间隔t 的函数。但是在实际问题中，我们常遇到的序列，特别是反映社会、经济现象的序列，大多数并不平稳，而是呈现出明显的趋势性或周期性。这时，我们就不能认为它是均值不变的平稳过程，需要用如下更一般的模型——t t t X Y μ=+来描述。其中,t μ表示t X 中随时间变化的均值,它往往可以用多项式、指数函数、正弦函数等描述，而t Y 是t X 中剔除趋势性或周期性t μ后余下的部分，往往可以认为是零均值的平稳过程，因而可以用ARMA 模型来描述。具体的处理方法可分为两大类：一类是通过某些数学方法剔除掉t X 中所包含的趋势性或周期性（即t μ），余下的t Y 可按平稳过程进行分析与建模，最后再经反运算由t Y 的结果得出t X 的有关结果。另一类方法是具体求出t μ的拟 合形式，求出t μ ?，然后对残差序列{t t X μ?-}进行分析，该残差序列可以认为是平稳的。利用前述方法可以求出t Y ?，最后综合可得t t t Y X μ???+=。如果我们对t μ的形式并不敢兴趣，则可以采取第一类方法，否则可以用第二类方法。需要再强调的一点是，时间序列非平稳性的表现是多种多样的，这里我们所能分析处理的仅是一些较为特殊的非平稳性。 二、建模原理 2.1平稳化方法 2.1.1差分 一般而言，若某序列具有线性的趋势，则可以通过对其进行一次差分而将线性趋势剔除掉，然后对差分后的序列拟合ARMA 模型进行分析与预测，最后再通过差分的反运算得到t X 的有关结果。做一次差分可记为t X ?，则 1--=?t t t X X X (1) 如果对一阶差分结果再进行差分，则称为高阶差分，差分的次数称为差分的阶，d 阶差分记为t d X ?。 2.2.2 季节差分 反映经济现象的序列，不少都具有周期性，例如，刚收获的小麦，由于供应充足，价格一般是较低的，然后随着供应量的减少，价格会逐渐上涨，直至下一个收获季节又重新开始这一周期。设t X 为一含有周期S 的周期性波动序列，则,2_,,s t s t t X X X ++…为各相应周期点的数值，它们则表现出非常相近或呈现某一趋

第三章平稳时间序列分析

t P p t t t t t x B x x B x Bx x ===---M 221第3章 平稳时间序列分析 一个序列经过预处理被识别为平稳非白噪声序列，那就说明该序列是一个蕴含着相关信息的平稳序列。 3.1 方法性工具 3.1.1 差分运算 一、p 阶差分 记 t x ?为t x 的1阶差分：1--=?t t t x x x 记t x 2 ?为t x 的2阶差分：21122---+-=?-?=?t t t t t t x x x x x x 以此类推：记 t p x ?为t x 的p 阶差分：111---?-?=?t p t p t p x x x 二、k 步差分 记t k x ?为t x 的k 步差分：k t t t k x x x --=? 3.1.2 延迟算子 一、定义 延迟算子相当与一个时间指针，当前序列值乘以一个延迟算子，就相当于把当前序列值的时间向过去拨了一个时刻。记B 为延迟算子，有 延迟算子的性质： 1. 10 =B 2.若c 为任一常数，有1 )()(-?=?=?t t t x c x B c x c B 3.对任意俩个序列{t x }和{t y }，有11)(--±=±t t t t y x y x B 4. n t t n x x B -= 5.)!(!!,)1()1(0 i n i n C B C B i n i i n n i i n -= -=-∑=其中 二、用延迟算子表示差分运算 1、p 阶差分 t p t p x B x )1(-=? 2、k 步差分 t k k t t t k x B x x x )1(-=-=?- 3.2 ARMA 模型的性质 3.2.1 AR 模型 定义 具有如下结构的模型称为p 阶自回归模型，简记为AR(p): t s Ex t s E Var E x x x x t s t s t t p t p t p t t t πΛ?=≠===≠+++++=---,0,0)(,)(,0)(,0222110εεεσεεφεφφφφε (3.4) AR(p)模型有三个限制条件： 条件一： ≠p φ。这个限制条件保证了模型的最高阶数为p 。 条件二： t s E Var E t s t t ≠===,0)(,)(,0)(2εεσεεε。这个限制条件实际上是要求随机干扰序列 }{t ε为 零均值白噪声序列。 条件三：t s Ex t s π?=,0ε。这个限制条件说明当期的随机干扰与过去的序列值无关。 通常把AR(p)模型简记为： t p t p t t t x x x x εφφφφ+++++=---Λ22110 (3.5)