三角形全等之倍长中线(类倍长二)(北师版)(含答案)

学生做题前请先回答以下问题

问题1：“三角形全等”的辅助线：

见中线，要________，________之后___________．

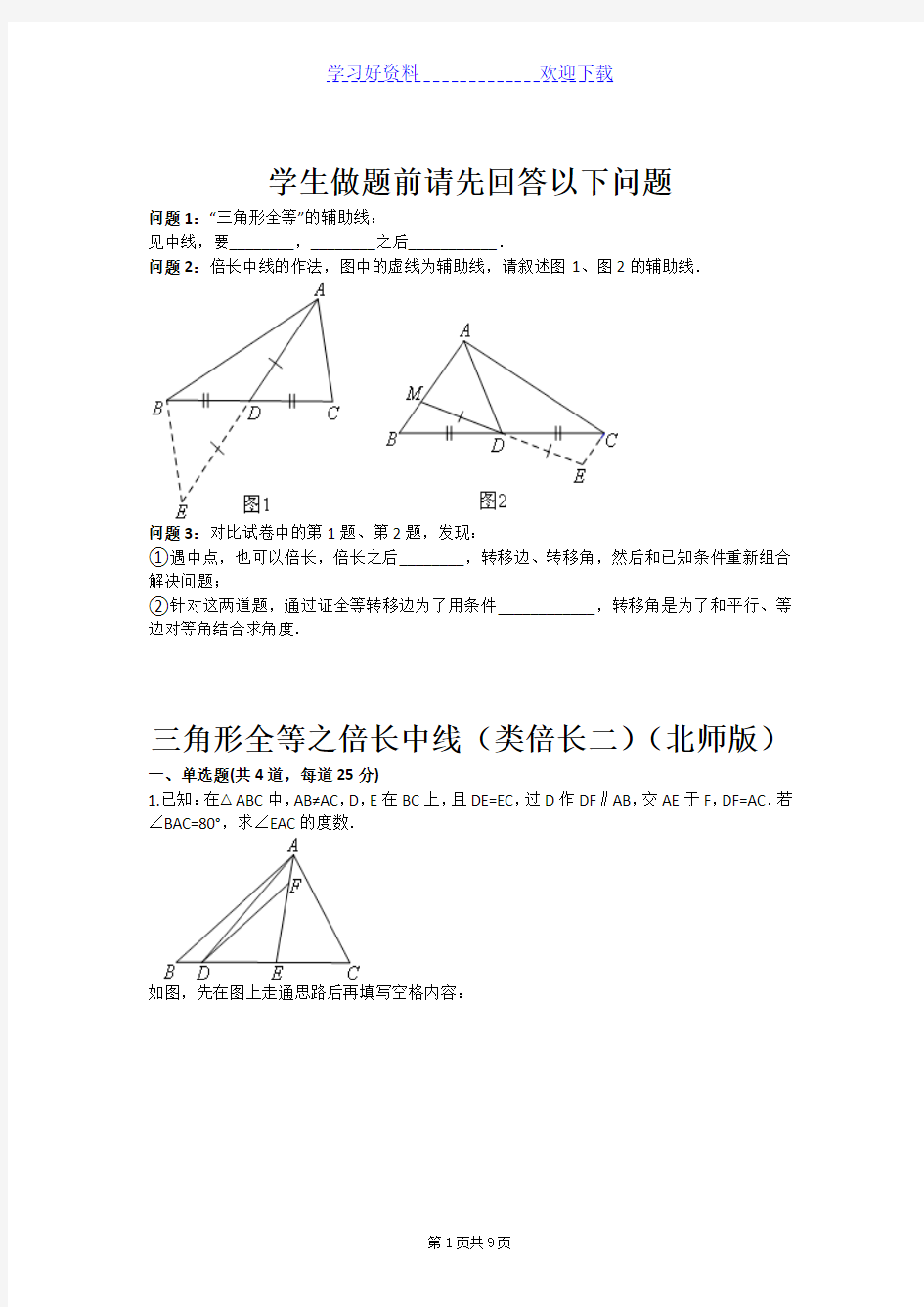
问题2：倍长中线的作法，图中的虚线为辅助线，请叙述图1、图2的辅助线．

问题3：对比试卷中的第1题、第2题，发现：

①遇中点，也可以倍长，倍长之后________，转移边、转移角，然后和已知条件重新组合解决问题；

②针对这两道题，通过证全等转移边为了用条件____________，转移角是为了和平行、等边对等角结合求角度．

三角形全等之倍长中线（类倍长二）（北师版）

一、单选题(共4道，每道25分)

1.已知：在△ABC中，AB≠AC，D，E在BC上，且DE=EC，过D作DF∥AB，交AE于F，DF=AC．若∠BAC=80°，求∠EAC的度数．

如图，先在图上走通思路后再填写空格内容：

①因为点E是DC的中点，考虑延长FE到点G，使EG=FE，连接CG；

②进而利用全等三角形的判定_________，证明_______≌_______；

③由全等可得________________；

④结合已知条件，得，从而∠EAC=40°．以上空缺处依次所填最恰当的是( )

A.②SAS，△BEA，△CDF；③AB=CG，AB∥CG；

B.②SAS，△DEF，△CEG；③DF=CG，DF∥CG；

C.②SAS，△BEA，△CDF；③AB=CG，∠DFE=∠G；

D.②SAS，△DEF，△CEG；③DF=CG，∠DFE=∠G；

答案：D

解题思路：

试题难度：三颗星知识点：三角形全等之倍长中线

2.已知：在△ABC中，AB≠AC，D，E在BC上，且DE=EC，过D作DF∥AB，交AE于F，DF=AC．若∠BAC=80°，求∠EAC的度数．

请你仔细观察下列序号所代表的内容：

①AC=DG，∠EAC=∠G；

②AC=DG，AE=GE；

③∠BAE=∠DFG；

④∠B=∠FDE．

以上空缺处依次所填最恰当的是( )

A.①③

B.①④

C.②③

D.②④

答案：A

解题思路：

试题难度：三颗星知识点：三角形全等之倍长中线

3.已知：如图，AD是△ABC的中线，DE平分∠ADB交AB于点E，DF平分∠ADC交AC于点F，连接EF．

求证：BE+CF＞EF．

如图，先在图上走通思路后再填写空格内容：

①因为点D是BC的中点，考虑延长FD到点G，使DG=DF，连接BG，EG；

②进而利用全等三角形的判定_________，证明_______≌_______；

③由全等可得________________；

④结合已知条件，得DE垂直平分GF，根据线段垂直平分线上的点到这条线段两个端点的距离相等，可得________________，最后利用三角形的三边关系可得BE+CF＞EF．

以上空缺处依次所填最恰当的是( )

A.②SAS，△BDG，△CDF；③BG=CF，∠DBG=∠C；④E G=EF

B.②SAS，△BDG，△CDF；③BG=CF；④EG=EF

C.②SAS，△BDG，△CDF；③BG=CF，DG=DF；④△EDG≌△FDE（AAS）

D.②SAS，△BDG，△CDA；③BG=CF；④EG=EF

答案：B

解题思路：

试题难度：三颗星知识点：三角形全等之倍长中线

4.已知：如图，AD是△ABC的中线，DE平分∠ADB交AB于点E，DF平分∠ADC交AC于点F，连接EF．

求证：BE+CF＞EF．

请你仔细观察下列序号所代表的内容：

①B E=CG，∠B=∠DCG；

②BE=CG；

③FE=FG；

④△EDF≌△GDF（AAS）．

以上空缺处依次所填最恰当的是( )

A.①③

B.①④

C.②③

D.②④

答案：C

解题思路：

试题难度：三颗星知识点：三角形全等之倍长中线

全等三角形之倍长中线法资料讲解

课题：《全等三角形之巧添辅助线——倍长中线法》 【方法精讲】常用辅助线添加方法一一倍长中线 △ ABC中，AD是BC边中线方式1 :直接倍长延长AD至U E， 例2: ABC中，AD是BAC的平分线，且BD=CD，求证AB=AC 方法1:作DE丄AB于E,作DF 丄AC于F,证明二次全等 方法2 :辅助线同上，利用面积 方法3 :倍长中线AD E 方式2 :间接倍长 作CF丄AD于F,作BE丄AD的延长线于E延长MD到 C 【经典例题】 例1 :△ ABC中，AB=5, AC=3求中线AD的取值范围. 提示：画出图形，倍长中线AD，利用三角形两边之和大于第三边 N,使DN=MD连接CN C 例3:已知在△ ABC中，AB=AC , D在AB 上, E在AC的延长线上，DE交BC于F,且DF=EF ,求证：BD=CE 方法1 :过D作DG // AE交BC于G,证明△ DGF^A CEF 使DE=AD，连接BE

方法2:过E 作EG // AB 交BC 的延长线于 G ,证明△ EFG^A DFB 方法3:过D 作DG 丄BC 于G,过E 作EHL BC 的延长线于 H,证明A BDG^A ECH 例4:已知在△ ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ,延长BE 交AC 于F ,求证：AF=EF 例5:已知：如图，在 ABC 中，AB 求证：AE 平分 BAC 方法1倍长AE 至G ,连结DG 方法2:倍长FE 至H ，连结CH 例 6:已知 CD=AB ，/ BDA= / BAD , AE 是厶 ABD 的中线，求证：/ C=Z BAE 提示：倍长 AE 至F ,连结DF,证明A ABE^A FDE ( SAS ,进而证明A ADF ^A ADC( SAS A 提示：倍长 AD 至G ,连接BG ,证明A BDG^A CDA 三角形BEG 是等腰三角形 AC , D E 在 BC 上,且 DE=EC 过 D 作 DF // BA 交 AE 于点 F , DF=AC. 第1题图

三角形全等专题倍长中线法

全等三角形基本判定条件： 1、三边对应相等 （SSS）。 2、两边夹角对应相等 （SAS） 3、两角夹边对应相等 （ASA）。 4、两角对边对应相等 （AAS） 5、直角三角形全等条件：① 斜边及一直角边对应相等（HL ）； ② 一直角边及一锐角对应相等（ASA ）或 斜边及一锐角对应相等（AAS ）； ③两直角边对应相等（SAS）。 ★注意：直角三角形全等，除边边边（SSS）,边角边（SAS）,角边角（ASA）, 角角边（AAS ）对应相等外，还有直角边及斜边（HL）、一直角边及一锐角（ASA）、斜边及一锐角（AAS）、两直角边（SS）等对应相等。 除以上基本判定外，全等三角形另外判定条件： 1、三条中线对应相等，两个三角形全等。 2、三条高线对应相等，两个三角形全等。 3、三条角平分线对应相等，两个三角形全等。 4、两个角及第三个角的角平分线对应相等，两个三角形全等。 5、两条边及第三条边上的中线对应相等，两个三角形全等。 6、钝角三角形中，一钝角和其一邻边对应相等，钝角所对的较大边也相等，两 个三角形全等。或两边及其中一边的对角（钝角）对应相等，两个三角形全等。（SSA） 7、等腰三角形中，底边和顶角分别对应相等，两个等腰三角形全等。 8、等腰直角三角形中，周长相等，两个等腰直角三角形全等。（因为等腰直角三角形三边之比为1: 1: √2故周长相等时，等腰直角三角形的对应角相等，对应边相等，故全等）。 9、等边三角形中，有一边对应相等，两个三角形全等。 ★特别提示：在三角形全等的判定中，一定有边相等，一定没有AAA和SSA （除非此角为钝角），这两种情况都不能唯一确定三角形的形状。 三角形全等的性质： 1. 全等三角形的对应角相等。 4. 全等三角形的对应边上的中线相等。 2. 全等三角形的对应边相等。 5.全等三角形的对应角的角平分线相等。 3. 全等三角形面积周长相等。 6.全等三角形的对应边上的高对应相等。 等腰三角形的性质 1、等腰三角形的两个底角度数相等（简写“等边对等角”）。 2、等腰三角形的顶角平分线，底边上的中线，底边上的高重合（简写“等腰三角形的三线合一性质”）。 3、等腰三角形的两底角平分线相等（两条腰上的中线相等，两条腰上的高相等）。 4、等腰三角形底边上的垂直平分线到两条腰的距离相等。 5、等腰三角形的一腰上的高与底边的夹角等于顶角的一半。 6、等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（等面积法证明）。

三角形全等之倍长中线(类倍长一)(人教版)(含答案)

学生做题前请先回答以下问题 问题1：“三角形全等”的辅助线： 见中线，要________，________之后___________，全等之后_________，_________． 问题2：倍长中线的作法，图中的虚线为辅助线，请叙述图1、图2的辅助线． 三角形全等之倍长中线（类倍长一）（人教版） 一、单选题(共4道，每道25分) 1.已知：如图，点E是BC的中点，∠BAE=∠D． 求证：AB=CD． 如图，先在图上走通思路后再填写空格内容： ①因为点E是BC的中点，考虑延长AE到点F，使EF=AE，连接CF； ②进而利用全等三角形的判定_________，证明_______≌_______； ③由全等可得________________；

④结合已知条件∠BAE=∠D，得∠F=∠D，在△DCF中，利用________________，可得CF=CD，等量代换得AB=CD． 以上空缺处依次所填最恰当的是( ) A.②SAS，△ABE，△ECF； ③AB=CF； ④等角对等边 B.②SAS，△ABE，△DEC； ③AB=CF，∠BAE=∠F； ④等边对等角 C.②SA S，△ABE，△FCE； ③∠ABE=∠FCE，∠BAE=∠F； ④等边对等角 D.②SAS，△ABE，△FCE； ③AB=FC，∠BAE=∠F； ④等角对等边 答案：D 解题思路：

试题难度：三颗星知识点：三角形全等之倍长中线 2.已知：如图，点E是BC的中点，∠BAE=∠D． 求证：AB=CD． 证明：如图，延长DE到点F，使EF=DE，连接BF．

∵E是BC的中点 ∴BE=CE 在△BEF和△CED中 ∴△BEF≌△CED（SAS） ∴____________________________ ∵∠BAE=∠D ____________________________ ∴AB=CD 请你仔细观察下列序号所代表的内容： ①BF=CD，∠EBF=∠C； ②BF=CD，∠F=∠D； ③； ④． 以上空缺处依次所填最恰当的是( ) A.①③ B.②③ C.①④ D.②④ 答案：B 解题思路：

人教版初中数学全等三角形倍长中线法和截长补短法

专题2：倍长中线法和截长补短法 例1：如图，AD 为△ABC 中BC 边上的中线（AB ＞AC ） （1）求证：AB ﹣AC ＜2AD ＜AB +AC ； （2）若AB=8cm ，AC=5cm ，求AD 的取值范围． 针对训练：1、在△ABC 中，AC=5，中线AD=7，则BC 边的取值范围是________________． 2、如图，AD 为△ABC 的中线，∠ADB 和∠ADC 的平分线分别交AB 、AC 于点E 、F ． 求证：BE +CF ＞EF ． 3．如图，点D 、E 三等分△ABC 的BC 边，求怔：AB +AC ＞AD +AE ． 例2：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF 针对训练：1.已知：如图，?ABC 中，∠C=90?，CM ⊥AB 于M ，AT 平分∠BAC 交CM 于D ，交BC 于T ，过D 作 DE//AB B

交BC 于E ，求证：CT=BE. 2、如图，已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：（1）AC=2AE （2）∠C=∠BAE 3、已知△ABC 中，AD 是BC 边上的中线，分别以AB 边、AC 边为直角边各向外作等腰直角三角形，求证：EF=2AD 例3、在△ABC 中，∠B=2∠C ，AD 是∠BAC 的平分线．求证：AC=AB +BD ． 针对训练： 1、如图，在△ABC 中，∠B=2∠C ，且AC=AB +BD ．求证：AD 是∠BAC 的平分线． D A B C M T E

全等三角形问题中常见的辅助线_倍长中线法

D C B A 全等三角形问题中常见的辅助线——倍长中线法 △ABC 中,AD 是BC 边中线 方式1：直接倍长，(图1)： 延长AD 到E ，使DE=AD ，连接BE 方式2：间接倍长 1) （图2）作CF ⊥AD 于F ，作BE ⊥AD 的延长线于E, 连接BE 2) （图3）延长MD 到N ，使DN=MD ，连接CD 【经典例题】 例1已知，如图△ABC 中，AB=5，AC=3， 则中线AD 的取值范围是_________. （提示：画出图形，倍长中线AD ，利用三角形两边之和大于第三边） 例2：已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上， DE 交BC 于F ，且DF=EF. 求证：BD=CE.（提示：方法1：过D 作DG ∥AE 交BC 于G ，证明ΔDGF ≌ΔCEF E D A B C F D C B A N D C B A M

E D F C B A 方法2：过E 作EG ∥AB 交BC 的延长线于G ，证明ΔEFG ≌ΔDFB 方法3：过D 作DG ⊥BC 于G ，过E 作EH ⊥BC 的延长线于H ，证明ΔBDG ≌ΔECH ） 例3、如图，△ABC 中，E 、F 分别在AB 、AC 上，DE ⊥DF ，D 是中点，试比较BE+CF 与EF 的大小.

变式：如图，AD 为ABC ?的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于F. 求证： EF CF BE >+ （提示：方法1：在DA 上截取DG=BD ，连结EG 、FG ， 证明ΔBDE ≌ΔGDE ΔDCF ≌ΔDGF 所以BE=EG 、CF=FG 利用三角形两边之和大于第三边 方法2： 倍长ED 至H ，连结CH 、FH ，证明FH=EF 、CH=BE ，利用三角形两边之和大于第三边） 例4：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF

最新倍长中线法(经典例题)

倍长中线法 知识网络详解： 中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线． 所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法． 倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS证全等（对顶角） 倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。 【方法精讲】常用辅助线添加方法——倍长中线 △ABC中 方式1：延长AD到 E，AD是BC边中线 使DE=AD， 连接BE 方式2：间接倍长 作CF⊥AD于F，延长MD到N， 作BE⊥AD的延长线于使DN=MD， 连接BE 连接CN 经典例题讲解： 例1：△ABC中，AB=5，AC=3，求中线AD的取值范围

例2：已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE 过D 作DG//AC 例3：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF 例4：已知：如图，在ABC ?中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC. 求证：AE 平分BAC ∠ B A B F D E C

例5：已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，求证：∠C=∠BAE 自检自测： 1、如图，△ABC中，BD=DC=AC,E是DC的中点，求证，AD平分∠BAE. 2、在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线相交于点F。试探究线段AB与AF、CF之间的数量关系，并证明你的结论. A B F E A B C

三角形全等之手拉手模型倍长中线截长补短法旋转寻找三角形全等方法归纳总结精修订

三角形全等之手拉手模型倍长中线截长补短法旋转寻找三角形全等方 法归纳总结 SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#

一、手拉手模型 要点一：手拉手模型 特点：由两个等顶角的等腰三角形所组成，并且顶角的 顶点为公共顶点 结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180° （3）OA平分∠BOC 变形： 例1.如图在直线ABC的同一侧作两个等边三角形ABD ?，连结AE与 ?与BCE CD，证明 （1）DBC ? ? ABE? (2)DC AE= (3)AE与DC之间的夹角为? 60 (4)DFB ? ? AGB? (5)CFB ? ? EGB? (6)BH平分AHC ∠ (7)AC GF//

变式精练1：如图两个等边三角形ABD ?，连结AE与CD， ?与BCE 证明（1）DBC ? ? ABE? （2）DC AE= （3）AE与DC之间的夹角为? 60 （4）AE与DC的交点设为H,BH平分AHC ∠ 变式精练2：如图两个等边三角形ABD ?， ?与BCE 连结AE与CD， 证明（1）DBC ABE? ? ? (2）DC AE= (3）AE与DC之间的夹角为? 60 (4）AE与DC的交点设为H,BH平分AHC ∠ 例2：如图，两个正方形ABCD与DEFG,连结 AG,,二者相交于点H CE 问：（1）CDE ADG? ?是否成立 ? （2）AG是否与CE相等 （3）AG与CE之间的夹角为多少度 （4）HD是否平分AHE ∠ 例3：如图两个等腰直角三角形ADC与 AG,,二者相交于点H EDG，连结CE 问：（1）CDE ?是否成立 ADG? ? （2）AG是否与CE相等 （3）AG与CE之间的夹角为多少度 （4）HD是否平分AHE ∠

截长补短与倍长中线法证明三角形全等

1.截长补短法证明三角形全等 例1已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证： AE=AD+BE 练习1如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。求证：BC=AB+DC。 AC-AB=2BE 2.已知∠ABC=3∠C，∠1=∠2，BE⊥AE，求证： 3如图，已知AD∥BC，∠P AB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．求 证：AD+BC=AB． P C E D B A

4在△ABC 中，?=∠90ACB ，BC AC =，直线MN 经过点C ，且MN AD ⊥于D ， MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时， 求证： ①ADC ?≌CEB ?；②BE AD DE +=； (2)当直线MN 绕点C 旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由. 6.如图,已知AC ∥BD ，EA 、EB 分别平分∠CAB 和∠DBA ，CD 过点E ，则AB 与AC+BD 相等吗？请说明理由 例2已知，如图1-1，在四边形ABCD 中，BC ＞AB ，AD =DC ，BD 平分∠ABC . 求证：∠BAD +∠BCD =180°. 例1. 练习已知，如图3-1，∠1=∠2，P 为BN 上一点，且PD ⊥BC 于点D ，AB +BC =2BD . 求证：∠BAP +∠BCP =180°. A B C D 图1-1 A P 1 2 N

2、倍长中线法证三角形全等 例1 、求证：三角形一边上的中线小于其他两边和的一半。 练习 1：△ABC 中，AB=5，AC=3，求中线AD 的取值范围 例2.已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE 练习2已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF 例3已知：如图，在ABC ?中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交 F E C A B D F E D A B C

三角形全等之倍长中线

三角形全等之倍长中线 课前预习 1. 填空 （1）三角形全等的判定有： 三边分别___________的两个三角形全等，即（____）； 两边和它们的_____分别相等的两个三角形全等，即（____）； 两角和它们的_____分别相等的两个三角形全等，即（____）； 两角和其中一个角的______分别相等的两个三角形全等，即（____）； 斜边和_______边分别相等的两个直角三角形全等，即（____）． （2）要证明两条边相等或者两个角相等，可以考虑放在两个三角形中证________；要证明两个三角形全等需要准备______组条件，这三组条件里面必须有______；然后依据判定进行证明，其中AAA ，SSA 不能证明两个三角形全． 2. 想一想，证一证 已知：如图，AB 与CD 相交于点O ，且O 是AB 的中点． （1）当OC =OD 时，求证：△AOC ≌△BOD ； （2）当AC ∥BD 时，求证：△AOC ≌△BOD ． O B C D A ? 知识点睛 1. “三角形全等”辅助线： 见中线，要__________，构造______________． 2. 中点的思考方向： ① （类）倍长中线 延长AD 到E ，使DE =AD ， 延长MD 到E ，使DE =MD ， 连接BE 连接CE D C B A M A B C D

②平行夹中点 F E D C B A 延长FE 交BC 的延长线于点G ? 精讲精练 1. 如图，在△ABC 中，AD 为BC 边上的中线． （1）按要求作图：延长AD 到点E ，使DE =AD ；连接BE ． （2）求证：△ACD ≌△EBD ． （3）求证：AB +AC >2AD ． （4）若AB =5，AC =3，求AD 的取值范围． 2. 如图，在△ABC 中，AD 平分∠BAC ，且BD =CD ． 求证：AB =AC ． 3. 如图，CB 是△AEC 的中线，CD 是△ABC 的中线，且AB =AC ． 求证：①CE =2CD ；②CB 平分∠DCE ． D C B A D B A D C B A

倍长中线法

全等三角形的类型题 常见辅助线的作法有以下几种： 1)遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”． 2)遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的 “旋转”． 3)遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”， 所考知识点常常是角平分线的性质定理或逆定理． 4)过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠” 5)截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，是之与特定线 段相等，再利用三角形全等的有关性质加以说明．这种作法，适合于证明线段的和、差、倍、分等类的题目．特殊方法：在求有关三角形的定值一类的问题时，常把某点到原三角形各顶点的线段连接起来，利用三角形面积的知识解答． 倍长中线法 1.已知：AB=4，AC=2，D是BC中点，AD是整数，求AD 2、已知：D是AB中点，∠ACB=90°，求证： 1 2 CD AB 3、已知：∠1=∠2，CD=DE，EF//AB，求证：EF=AC 4、已知，E是AB中点，AF=BD，BD=5，AC=7，求DC A D B C D A B C B A C D F 2 1 E

截长补短法 1、已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C 2、如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。求证：BC=AB+DC 。 3、如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ． 4、已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BE 边加减的问题 1、已知：点A 、F 、E 、C 在同一条直线上， AF ＝CE ，BE ∥DF ，BE ＝DF ．求证：△ABE ≌△CDF ． 2、如图：DF=CE ，AD=BC ，∠D=∠C 。求证：△AED ≌△BFC 。 C D B F A E D C B A F E D C P E D C B A

全等三角形之中线倍长法讲课讲稿

授课教案 教学标题 教学目标 教学重难点 上次作业检查 授课内容：— 一.热身训练 1. 如图，已知：AD 是BC 上的中线，且DF=DE 求证：BE // CF. 2. 如图，AE BC 交于点 M, F 点在AM 上，BE / CF, BE=CF 求证：人“是厶ABC 的中线. 3. AB=AC , DB=DC F 是AD 的延长线上的一点。求证： BF=CF 4. 如图：AB=CD AE=DF CE=FB 求证：AF=DE 5. 已知：如图所示， AB = AD BC = DC E 、F 分别是 DC BC 的中点，求证： AE = AF. 二.知识梳理 1?中点的定义 2?中点的表示方法：等量关系、倍的关系、分的关系 3?三角形中线的作用：等分面积 全等） 三?典型例题 例1.（“希望杯”试题）已知，如图△ ABC 中, AB=5 AC=3则中线AD 的取值范围是 _____________ . 分析：①将AD 边放在某个三角形中，利用三边关系求出取值范围； A ② 中线倍长法的具体应用：延长 AD 至M,使DM=AD 连接BM 利用SAS 证明三、 角形全等； ③ 将线段AC 转换成BM 在厶ABM 中利用三边关系求出 2AD 取值范 ——L \ 中线倍长法证明全等 熟练掌握有中点为背景的全等三角形证明的方法 重点掌握中线倍长法模型的建立，能利用中线倍长法解决问题 4?全等三角形中中线的作用：倍长中线（延长中线至 *，连接**，利用SAS 证明三角形

例2.如图：在厶ABC中，BA=BC D是AC的中点。求证：BDL AC. 分析：中线倍长法，延长BD至M,使DM=BD连接AM,两次全 等，再证明角相等. 1 例3.已知：D是AB中点，/ ACB=90,求证：CD AB 2 分析：中线倍长法，延长CD至M,使DM=CD连接AM, 两次全等，解决线段分的证明 例4.已知，E 是AB 中点，AF=BD, BD=5, AC=7,求DC 分析：中线倍长法，E为中点，可倍长DE FE、CE至M （具体是哪条线段尝试之后再引导学生下结论），连接AM，利用SAS证明三角形全等，有部分等腰三角形的知识参与解题，可引导学生回忆三角形按边分类时所传授的等腰三角形的知识 D 四?课堂练习 1. 已知：AB=4, AC=2 D是BC中点，AD是整数, 2. 已知：/ 仁/2, CD=DE EF//AB，求证：EF： 五?课后反思： 1. 三角形全等证明的方法，注意两次全等的问题； 2. 有中点为背景参与的问题，常见思路是“中线倍长法”

倍长中线构造全等三角形

巧添辅助线——倍长中线 【夯实基础】 例:ABC ?中,AD 就是BAC ∠的平分线,且BD=CD,求证AB=AC 方法1:作D E ⊥AB 于E,作D F ⊥AC 于F,证明二次全等 方法2:辅助线同上,利用面积 方法3:倍长中线AD 【方法精讲】常用辅助线添加方法——倍长中线 △ABC 中 方式1: 延长AD 到E, AD 就是BC 边中线 使DE=AD, 连接BE 方式2:间接倍长 作CF ⊥AD 于延长MD 到N, 作BE ⊥AD 的延长线于使DN=MD, 连接BE 连接CD 【经典例题】 例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围 提示:画出图形,倍长中线AD,利用三角形两边之与大于第三边 例2:已知在△ABC 中,AB=AC,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F,且DF=EF,求证:BD=CE 方法1:过D 作DG ∥AE 交BC 于G,证明ΔDGF ≌ΔCEF 方法2:过E 作EG ∥AB 交BC 的延长线于G,证明ΔEFG ≌ΔDFB 方法3:过D 作DG ⊥BC 于G,过E 作EH ⊥BC 的延长线于H 证明ΔBDG ≌ΔECH

例3:已知在△ABC 中,AD 就是BC 边上的中线,E 就是AD 上一点,且BE=AC,延长BE 交AC 于F,求 证:AF=EF 提示:倍长AD 至G ,连接BG,证明ΔBDG ≌ΔCDA 三角形BEG 就是等腰三角形 例4:已知:如图,在ABC ?中,AC AB ≠,D 、E 在BC 上,且DE=EC,过D 作BA DF //交AE 于点F,DF=AC 、 求证:AE 平分BAC ∠ 提示: 方法1:倍长AE 至G,连结DG 方法2:倍长FE 至H,连结CH 例5:已知CD=AB,∠BDA=∠BAD,AE 就是△ABD 的中线,求证:∠C=∠BAE 提示:倍长AE 至F,连结DF 证明ΔABE ≌ΔFDE(SAS) 进而证明ΔADF ≌ΔADC(SAS) 【融会贯通】 1、在四边形ABCD 中,AB ∥DC,E 为BC 边的中点,∠BAE=∠EAF,AF 与DC 的延长线相交于点F 。试探究线段AB 与AF 、CF 之间的数量关系,并证明您的结论 提示:延长AE 、DF 交于G 证明AB=GC 、AF=GF 所以AB=AF+FC B 第 1 题图 A B F D E C

珍藏二——_全等三角形证明辅助线作法之倍长中线问题

几何综合部分倍长中线问题 巧添辅助线——倍长中线 【夯实基础】 例：ABC ?中，AD是BAC ∠的平分线，且BD=CD，求证AB=AC 方法1：作D E⊥AB于E，作D F⊥AC于F，证明二次全等 方法2：辅助线同上，利用面积 方法3：倍长中线AD 【方法精讲】常用辅助线添加方法——倍长中线 △ABC中方式1：延长AD到E， AD是BC边中线使DE=AD， 连接BE 方式2：间接倍长

几何综合部分倍长中线问题 2 作CF⊥AD于F，延长MD到N， 作BE⊥AD的延长线于E 使DN=MD， 连接BE 连接CD 【经典例题】 例1：△ABC中，AB=5，AC=3，求中线AD的取值范围 例2：已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且 BD=CE 例3：已知在△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC，延长BE交AC于F，求证：AF=EF B

几何综合部分 倍长中线问题 3 提示：倍长AD 至G ，连接BG ，证明ΔBDG ≌ΔCDA 三角形BEG 是等腰三角形 例4：已知：如图，在ABC ?中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC. 求证：AE 平分BAC ∠ 提示： 方法1：倍长AE 至G ，连结DG 方法2：倍长FE 至H ，连结CH 例5：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE 提示：倍长AE 至F ，连结DF 证明ΔABE ≌ΔFDE （SAS ） 进而证明ΔADF ≌ΔADC （SAS ） 第 1 题图 A B F D E C

全等三角形之手拉手模型、倍长中线-截长补短法

手拉手模型 要点一：手拉手模型 特点：由两个等顶角的等腰三角形所组成，并且顶角的 顶点为公共顶点 结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180° （3）OA 平分∠BOC 变形： 例1.如图在直线ABC 的同一侧作两个等边三角形ABD ?与BCE ?，连结AE 与CD ，证明 （1）DBC ABE ??? (2)DC AE = (3)AE 与DC 之间的夹角为? 60 (4)DFB AGB ??? (5)CFB EGB ??? (6)BH 平分AHC ∠ (7)AC GF // 变式精练1：如图两个等边三角形ABD ?与BCE ?，连结AE 与CD ， 证明（1）DBC ABE ???

（2）DC AE = （3）AE 与DC 之间的夹角为? 60 （4）AE 与DC 的交点设为H ,BH 平分AHC ∠ 变式精练2：如图两个等边三角形ABD ?与BCE ?，连结AE 与CD ， 证明（1）DBC ABE ??? (2）DC AE = (3）AE 与DC 之间的夹角为?60 (4）AE 与DC 的交点设为H ,BH 平分AHC ∠ 例2：如图，两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H 问：（1）CDE ADG ???是否成立？ （2）AG 是否与CE 相等？ （3）AG 与CE 之间的夹角为多少度？ （4）HD 是否平分AHE ∠？ 例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交 于点H 问：（1）CDE ADG ???是否成立？ （2）AG 是否与CE 相等？

（3）AG 与CE 之间的夹角为多少度？ （4）HD 是否平分AHE ∠？ 例4：两个等腰三角形ABD ?与BCE ?，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ， 问：（1）DBC ABE ???是否成立？ （2）AE 是否与CD 相等？ （3）AE 与CD 之间的夹角为多少度？ （4）HB 是否平分AHC ∠？ 倍长与中点有关的线段 倍长中线类 ?考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的。 【例1】 已知：ABC ?中，AM 是中线．求证：1 ()2 AM AB AC <+． M C B A 【练1】在△ABC 中，59AB AC ==，，则BC 边上的中线AD 的长的取值范围是什么？ 【练2】如图所示，在ABC ?的AB 边上取两点E 、F ，使AE BF =，连接CE 、CF ，求证：AC BC +>EC FC +．

全等三角形之倍长中线法

全等三角形之倍长中线 1. 如图，AD 为△ABC 的中线． （1）求证：AB +AC >2AD ． （2）若AB =5，AC =3，求AD 的取值范围． 2. 如图，在△ABC 中，AD 平分∠BAC ，且BD =CD ． 求证：AB =AC ． 3. 如图，CB 是△AEC 的中线，CD 是△ABC 的中线，且AB =AC ． 求证：①CE =2CD ；②CB 平分∠DCE ． D C B A C A D B A

4. 如图，在△ABC 中，D 是BC 边的中点，E 是AD 上一点，BE =AC ， BE 的延长线交AC 于点F ． 求证：∠AEF =∠EAF ． 5. 如图，在△ABC 中，AD 交BC 于点D ，点E 是BC 的中点，EF ∥AD 交CA 的延长线于点F ，交 AB 于点G ，BG =CF ． 求证：AD 为△ABC 的角平分线． 6. 如图，在四边形ABCD 中，AD ∥BC ，点E 在BC 上，点F 是CD 的中 点，且AF ⊥AB ，已知AD =2.7，AE =BE =5，求CE 的长． 7. 如图，在正方形ABCD 的边CB 的延长线上取一点E ，△FEB 为等腰直角三角形，∠FEB =90°， 连接FD ，取FD 的中点G ，连接EG ，CG ． 求证：EG =CG 且EG ⊥CG ． 1. 已知：如图，在梯形ABCD 中，AD ∥BC ，AB =AD +BC ，E 是CD 的中点． 求证：AE ⊥BE ． F E D C A G F E D A F E D C B A G F E D C B A E D C B A

倍长中线构造全等三角形

倍长中线构造全等三角 形 -CAL-FENGHAI.-(YICAI)-Company One1

巧添辅助线——倍长中线 【夯实基础】 例：ABC ?中，AD是BAC ∠的平分线，且BD=CD，求证AB=AC 方法1：作DE⊥AB于E，作DF⊥AC于F，证明二次全等方法2：辅助线同上，利用面积 方法3：倍长中线AD 【方法精讲】常用辅助线添加方法——倍长中线 △ABC中 AD到E， AD是BC边中线， 连接BE 方式2 ⊥AD于F， AD的延长线于 连接 【经典例题】 例1：△ABC中，AB=5，AC=3，求中线AD的取值范围 提示：画出图形，倍长中线AD，利用三角形两边之和大于第三边 例2：已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且DF=EF，求证：BD=CE 方法1：过D作DG∥AE交BC于G，证明ΔDGF≌ΔCEF 方法2：过E作EG∥AB交BC的延长线于G，证明ΔEFG 方法3：过D作DG⊥BC于G，过E作EH⊥BC 证明ΔBDG≌ΔECH 2

3 例3：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交 AC 于F ，求证：AF=EF 提示：倍长AD 至G ，连接BG ，证明ΔBDG ≌ΔCDA 三角形BEG 是等腰三角形 例4：已知：如图，在ABC ?中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC. 求证：AE 平分BAC ∠ 提示： 方法1：倍长AE 至G ，连结DG 方法2：倍长FE 至H ，连结CH 例5：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE 提示：倍长AE 至F ，连结DF 证明ΔABE ≌ΔFDE （SAS ） 进而证明ΔADF ≌ΔADC （SAS ） 【融会贯通】 1、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。试探究线段AB 与AF 、CF 之间的数量关系，并证明你的结论 提示：延长AE 、DF 交于G 证明AB=GC 、AF=GF 所以AB=AF+FC B 第 1 题图 A B F D E C

全等三角形辅助线之倍长中线法

全等三角形辅助线之倍 长中线法 -CAL-FENGHAI.-(YICAI)-Company One1

全等三角形辅助线之倍长中线法 倍长中线法：遇中线，要倍长，倍长之后有全等． 当倍长后，连接方式不一样，可以产生更多结论如下： 与倍长中线法类似的辅助线作法 M A B C D E MD E MD=DE CE BDM CDE BM CE ???延长至，使，连接可证，AD ABC ?为的中线 D C B A E AD E AD=DE CE BE CE ABEC 延长至，使，当连接时，结论相似；　 当连接、，则为平行四边形 AD E DE=AD BE ADC EDB AD=DE ADC=EDB BD=CD ADC EDB(SAS)AC BE ??∠∠???延长至使，连接在和中 ，，故与此相关的重要结论AD ABC ?为的中线 D C B A E

举例： 如图，在△ABC 中，AD 为BC 边上的中 D C B A E AD E DE=AD BE ADC EDB AD=DE ADC=EDB BD=CD ADC EDB(SAS) AB-BE AE AB+BE AE

如图，在△ABC 中，D 是BC 的中点，E 是AD 上一点，BE=AC ，BE 的延长线交AC 于点F ．求证：∠AEF=∠EAF． F E D C B A 321 M A B C D E F

初中几何模型3(中点模型-倍长中线法)

初中几何模型3（中点模型－倍长中线法） 1、如图，在△ABC 中，AD 平分∠BAC ，且BD =CD ．求证：AB =AC ． 方法1：作D E ⊥AB 于E ，作D F ⊥AC 于F ，证明二次全等 方法2：辅助线同上，利用面积 方法3：倍长中线AD 2、如图，CB 是△AEC 的中线，CD 是△ABC 的中线，且AB =AC ． 求证：①CE =2CD ；②CB 平分∠DCE ． 3、 已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC 4、如图，在△ABC 中，D 是BC 边的中点，E 是AD 上一点，BE =AC ，BE 的延长线交AC 于点F ．求证：∠AEF =∠EAF ． E D C B F E D C A F A E D C B D B A

5、如图，在四边形ABCD 中，AD ∥BC ，点E 在BC 上，点F 是CD 的中点，且AF ⊥AB ，已知AD =2.7，AE =BE =5，求CE 的长． 6、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。试探究线段AB 与AF 、CF 之间的数量关系，并证明你的结论 7、如图，AD 为ABC ?的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于F. 求证：EF CF BE >+ 8、如图所示，在四 边形ABCD 中，AD ∥BC ，CD ∥BA E 是BC 边的中点，连接AE ，F 为CD 边上一点，且满足∠DFA=2∠BAE. （1）若∠D=105°，∠DAF=35°，求∠FAE 的度数；（2）求证：AF=CD+CF. F E D C B A 第 14 题图 D F C B E A F E D C B A

倍长中线法经典例题)

倍长中线法 知识网络详解： 中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线． 所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法． 倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS 证全等（对顶角） 倍长中线最重要的一点，延长中线一倍，完成SAS 全等三角形模型的构造。 【方法精讲】常用辅助线添加方法——倍长中线 △ABC 中 方式1： 延长AD 到E ， AD 是BC 边中线 使DE=AD ， 连接BE 方式2：间接倍长 作CF ⊥AD 于F ， 延长MD 到 N ， 作BE ⊥AD 的延长线于E 使DN=MD ， 连接BE 连接CN 经典例题讲解： 例1：△ABC 中，AB=5，AC=3，求中线AD 的取值范围 D A B C E D A B C F E D C B A N D C B A M

例2：已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE 例3：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF 例4：已知：如图，在ABC ?中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC. 求证：AE 平分BAC ∠ F E D A B C F E C A B D A B F D E C

1初中数学《几何辅助线秘籍》中点模型的构造1(倍长中线法;构造中位线法)资料

精品文档 学生姓名上课时间 学生年级 辅导老师 学校 科目 教学重点教学目标中点模型的构造（倍长中线法；构造中位线法；构造斜边中线法）系统有序掌握几何求证思路，掌握何时该用何种方法做辅助线 开场：1.行礼；2.晨读；3.检查作业；4.填写表格 新课导入知识点归纳 1.已知任意三角形（或者其他图形）一边上的中点，可以考虑：倍长中线法（构造全等三角形）； 2.已知任意三角形两边的中点，可以考虑：连接两中点形成中位线； 3.已知直角三角形斜边中点，可以考虑：构造斜边中线； 4.已知等腰三角形底边中点，可以考虑：连接顶点和底边中点利用“三线合一”性质. 做辅助线思路一：倍长中线法 经典例题1：如图所示，在△ABC中，AB＝20，AC＝12，求BC边上的中线AD的取值范围. 【课堂训练】 1.如图，已知CB、CD分别是钝△角AEC和锐角△ABC的中线，且AC＝AB，给出下列结论： ①AE＝2AC；②CE＝2CD；③∠ACD＝∠BCE；④CB平分∠DCE，则以上结论正确的是（） A.①②④ B.①③④ C.①②③ D.①②③④ 新 课 内 容 第1题图第2题图 2.如图，在正方形A BCD中，E为AB边的中点，G、F分别为AD，BC边上的点，若A G＝1， BF＝2，∠GEF＝90°，则GF的长为（） A. 2 B. 3 C. 4 D. 5 3.如图，在△ABC中，点D、E为边BC的三等分点，则下列说法正确的有（） ①BD＝DE＝EC；②AB＋AE＞2AD；③AD＋AC＞2AE；④AB＋AC＞AD＋AE。 A. 1个 B. 2个 C. 3个 D. 4个

4.如图，在△ABC中，AB＞BC，E为BC边的中点，AD为∠BAC的平分线，过E作AD的平行线，交AB于F，交CA的延长线于G，求证：BF＝CG． G B A F E D C 5.如图所示，已知在△ABC中，AD是BC边上的中线，F是AD上的一点，连接BE并延长交AC 于点F，AE＝EF，求证：AC＝BF. A E F B D C 6.如图所示，在△ABC中，分别以AB、AC为直角边向外做等腰直角三角△形ABD和△ACE，F 为BC边上中点，FA的延长线交DE于点G，求证：①DE＝2AF；②FG⊥DE． D G E A B F C

全等三角形问题中常见的辅助线倍长中线法

全等三角形问题中常见的辅助线一一倍长 中线法 △ ABC中,AD是BC边中线 方式1 :直接倍长，（图1）:延长AD到E,使DE=AD连接BE 方式2 :间接倍长 1）（图2）作CF丄AD于F,作BE X AD的延长线于E,连接BE 2）（图3）延长MD到N,使DN=MD连接CD 【经典例题】 例1已知，如图△ ABC中，AB=5 AC=3 贝忡线AD的取值范围是___________ . （提示：画出图形，倍长中线AD,利用三角形两边之和大于第三边）例2 :已知在厶ABC中, AB=AC D在AB上, E在AC的延长线上, DE 交BC于F, 且DF=EF. A

例4:已知在厶ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC延 长BE交AC于F,求证：AF=EF 求证：BD=CE.（提示：方法 1 :过D作DG/ AE交BC于G 证明△ DGF^A CEF 方法2 :过E作EG// AB交BC的延长线于G,证明A EFG^A DFB 方法3 :过D作DGL BC于G,过E作EH丄BC的延长线于H,证明A BDG^A ECH 例3、如图，△ ABC中, E、F分别在AB AC上，DEL DF, D是中点，试比较BE+与EF的大小. B 变式：如图，AD为ABC的中线，DE平分BDA交AB于E, DF平分ADC交AC于 F. A求证: （提示：方法1:在DA上截取DG=BD连结EG FQ 证明A BDE^A GDE A4A DGF所以BE=EG EF CF=FG 利用三角形两边之和大于第三边方法2: 倍长ED至H,连结CH FH,证明 FH=EF C D C E E CF B