第十次课程 噪声分析与傅里叶分析

第十次课程 噪声分析与傅里叶分析

第一部分 噪声分析

一、噪声分析功能

噪声分析就是针对电路中无法避免的噪声所做的分析，它是与交流分析一起使用的。电路中所计算的噪声通常是电阻上产生的热噪声、半导体元件产生的散粒噪声和闪烁噪声。 二、噪声分析

为了定量表征电路中的噪声大小，PSpice 程序AC 分析的每个频率点上对指定输出端计算出等效输入噪声。等效噪声相当于是将电路中所有的噪声源都集中到选定的独立电压源（或电流源）处。其作用大小相当于是在输入独立源处加上大小等于等效噪声的噪声源，则在节点处产生的输出噪声大小正好等于实际电路中所有噪声源在输出节点处产生的噪声。输出和输入噪声电平都对噪声带宽的平方根进行归一化，噪声电压的单位是V/sqrt(HZ), 噪声电流的单位是A/sqrt （HZ ）。

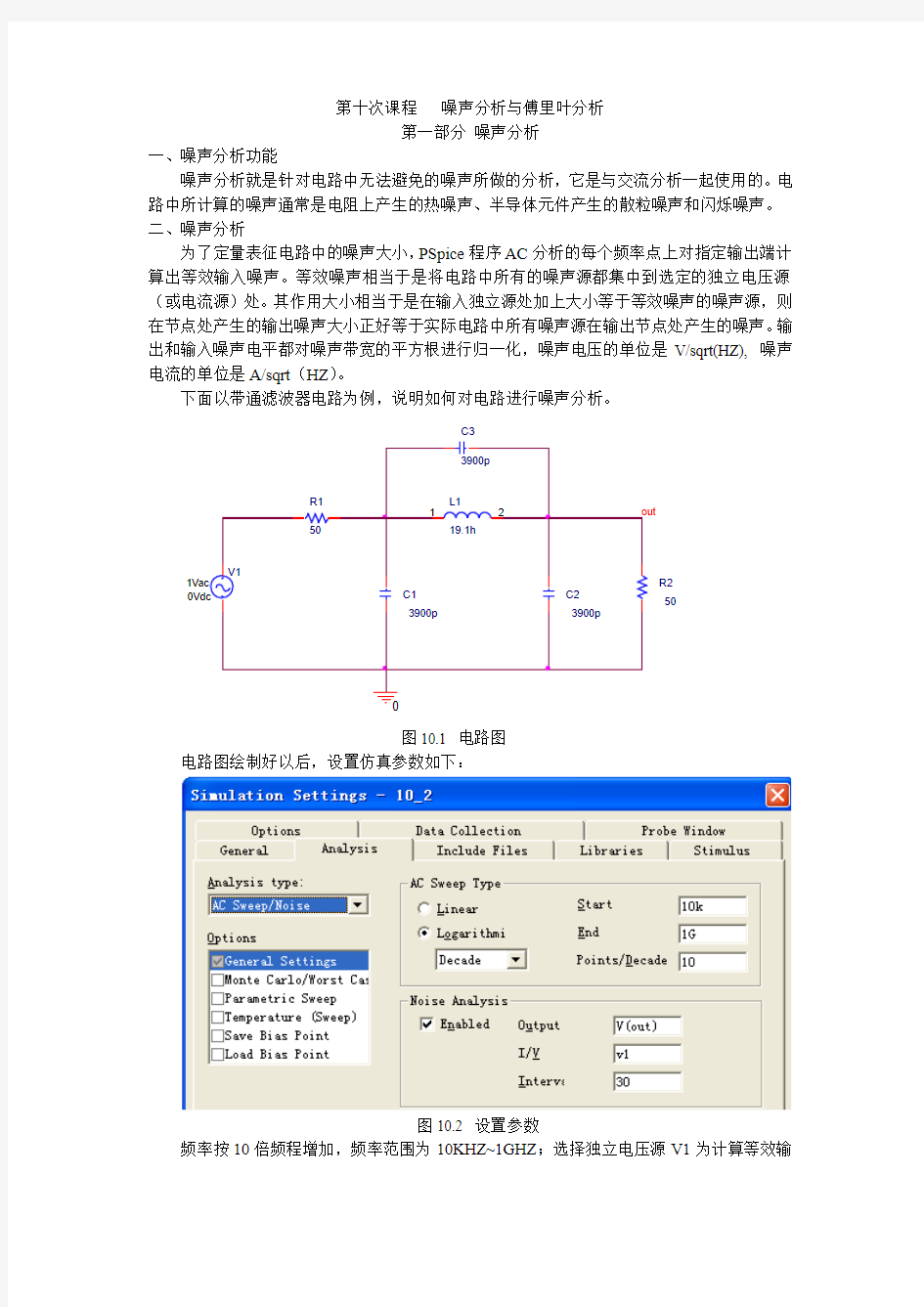
下面以带通滤波器电路为例，说明如何对电路进行噪声分析。

C3

R250

图10.1 电路图 电路图绘制好以后，设置仿真参数如下：

图10.2 设置参数

频率按10倍频程增加，频率范围为10KHZ~1GHZ ；选择独立电压源V1为计算等效输

入噪声的位置，对V（out）点作噪声分析（也就是说将out出处的等效输出电压除以从V1到V(out)的增益就得到在V1处的等效输入噪声，V1只计算输入等效噪声源的位置，其本身并不是噪声源）；在Interval栏中设置30，表示每隔30个点频详细输出电路中每一个噪声源在输出节点处产生的噪声分量大小，同时给出输出节点处的总噪声均方根值以及输入等效噪声的大小。噪声分析的结果只存入.out输出文件。噪声分析不涉及Probe数据文件。表10.1列出了噪声分析的具体参数设置的意义，由于噪声分析与交流分析是同时进行的，因此噪声分析与交流分析的参数设置是相同的。

三噪声分析输出结果

设置完参数之后，执行仿真程序，在图形窗口中添加输入和输出等效噪声电压波形如下图所示。

图10.3 输入等效噪声电压波形图

图10.4 输出等效噪声电压波形图

第二部分 傅里叶分析

一、傅里叶分析功能

在时域分析和交流分析里提供了傅里叶分析功能。傅里叶分析是对输出波形的最后一个周期（系统默认设置）进行谐波分析，计算出直流分量、基波、各次谐波分量以及失真度。 二、傅里叶分析

新建工程文件，如图10.5所示。正弦电压源V1的参数为：VOFF=0,VAMPL=10,FREQ=100,PHASE=0.

VOFF = 0C11

L1

R1

图10.5电路图

新建仿真文件，仿真设置如下图10.6所示。设置仿真开始时间为0，仿真到20ms ，步长为0.1ms 。因为设置仿真时间比较短，电路仍处于瞬态过程。

图10.6 仿真设置

在图10.6所示的仿真参数设置对话框里，点击“Output File Options”按钮，打开输出文件设置对话框，如图10.7所示。选择“Perform Fourier Anal”，设定基波为100HZ，这样输出文件里会以100HZ为基准进行归一化计算，谐波次数取到10次，所分析的变量是流过R1的电流I(R1).

图10.7 输出文件选项

仿真参数设置好后，在R1的节点上放置电流探针，运行仿真程序，输出I(R1)的时域波形如图10.8所示。

图10.8 I(R1)波形

点选“傅里叶分析”快捷按钮，出现傅里叶分析结果。为了便于观察，将横轴的坐标范围设置为0到1000HZ。点选Plot/Axis Settings…菜单，打开坐标设置对话框，如图10.9所示。在坐标设置对话框里，Data Range选择User Define，范围从0到1KHZ，单击“OK”，

傅里叶分析结果如图10.10所示。

图10.9 自定义横轴坐标

图10.10 调整坐标后傅里叶分析结果从图10.10可以清楚地看出波形中主要包含直流分量和基波。

点选View/Output File菜单或者快捷方式，打开输出文件，其中傅里叶分析结果如图10.11所示。从文件里可以看到I(R1)的直流分量是13.70275Ma,，基波直到10次谐波的幅值和相位以及归一化后的幅值相位均列表显示，最后给出了总的谐波失真系数。

图10.11 输出文件的傅里叶分析数据

上面的仿真时间只取了20ms，由于时间比较短，电路的瞬态过程没有结束。

下面修改仿真参数，把仿真时间设置为从0~10s，步长为100ms，运行后输出的I(R1)波形如图10.12所示。对其进行傅里叶分析，结果如图10.13所示。可以清楚地看到此时直流分量很小，可以认为电路已处于正弦稳态。输出文件里的傅里叶分析数据如图10.14所示。

图10.12 I(R1)仿真波形

图10.13 10s时傅里叶分析结果

图10.1410s时傅里叶分析数据

傅里叶(Fourier)级数的指数形式与傅里叶变换

傅里叶(Fourier )级数的指数形式与傅里叶变换 专题摘要：根据欧拉（Euler ）公式，将傅里叶级数三角表示转化为指数表示，进而得到傅里叶积分定理，在此基础上给出傅里叶变换的定义和数学表达式。 在通信与信息系统、交通信息与控制工程、信号与信息处理等学科中，都需要对各种信号与系统进行分析。通过对描述实际对象数学模型的数学分析、求解，对所得结果给以物理解释、赋予其物理意义，是解决实际问题的关键。这种数学分析方法主要针对确定性信号的时域和频域分析，线性时不变系统的描述以及信号通过线性时不变系统的时域分析与变换域分析。所有这些分析方法都离不开傅里叶变换、拉普拉斯变换和离散时间系统的z 变换。而傅里叶变换的理论基础是傅里叶积分定理。傅里叶积分定理的数学表达式就是傅里叶级数的指数形式。 不但傅里叶变换依赖于傅里叶级数，就是纯数学分支的调和分析也来源于函数的傅里叶级数。因此，傅里叶级数无论在理论研究还是在实际应用中都占有非常重要的地位。我们承认满足狄里克莱（Dirichlet ）条件下傅里叶级数的收敛性结果，不去讨论和深究傅里叶展式的唯一性问题。 傅里叶级数的指数形式 一个以T 为周期的函数)(t f ，在]2 ,2[T T 上满足狄里克莱条件：1o

)(t f 连续或只有有限个第一类间断点；2o 只有有限个极值点。那么)(t f 在]2 ,2[T T - 上就可以展成傅里叶级数。在连续点处 ∑∞ =++=1 )sin cos (2)(n n n t n b t n a a t f ωω， （1） 其中 T πω2= ， ),2,1,0(,cos )(2 22Λ==?-n dt t n t f T a T T n ω， （2） ),3,2,1(,sin )(2 22 Λ==?-n dt t n t f T b T T n ω， （3） 根据欧拉（Euler ）公式：θθθsin cos j e j +=，（1）式化为 ∑∞=--?? ????-+++=10222)(n t jn t jn n t jn t jn n j e e b e e a a t f ωωωω ∑∞=-?? ? ???++-+=10222n t jn n n t jn n n e jb a e jb a a ωω， （4） 若令 dt t f T c T T ?-=22 0)(1 Λ,3,2,1,)(1 ]sin )[cos (1 sin )(1cos )(1222 2222 22==-=-=-=????-----n dt e t f T dt t n j t n t f T dt t n t f T j dt t n t f T jb a c T T t jn T T T T T T n n n ωωωωω Λ,3,2,1,)(1 22 ==?--n dt e t f T c T T t jn n ω 综合n n c c c -,,0，可合并成一个式子 Λ,2,1,0,)(1 22 ±±==?--n dt e t f T c T T t jn n ω， （5）

傅里叶分析报告教程(完整版)

傅里叶分析之掐死教程（完整版）更新于2014.06.06 Heinrich · 6 个月前 作者：韩昊知乎：Heinrich 微博：@花生油工人知乎专栏：与时间无关的故事 谨以此文献给大连海事大学的吴楠老师，柳晓鸣老师，王新年老师以及张晶泊老师。 转载的同学请保留上面这句话，谢谢。如果还能保留文章来源就更感激不尽了。 我保证这篇文章和你以前看过的所有文章都不同，这是12年还在果壳的时候写的，但是当时没有来得及写完就出国了……于是拖了两年，嗯，我是拖延症患者…… 这篇文章的核心思想就是： 要让读者在不看任何数学公式的情况下理解傅里叶分析。 傅里叶分析不仅仅是一个数学工具，更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是，傅里叶分析的公式看起来太复杂了，所以很多大一新生

上来就懵圈并从此对它深恶痛绝。老实说，这么有意思的东西居然成了大学里的杀手课程，不得不归咎于编教材的人实在是太严肃了。（您把教材写得好玩一点会死吗？会死吗？）所以我一直想写一个有意思的文章来解释傅里叶分析，有可能的话高中生都能看懂的那种。所以，不管读到这里的您从事何种工作，我保证您都能看懂，并且一定将体会到通过傅里叶分析看到世界另一个样子时的快感。至于对于已经有一定基础的朋友，也希望不要看到会的地方就急忙往后翻，仔细读一定会有新的发现。 ——————————————以上是定场诗—————————————— 下面进入正题： 抱歉，还是要啰嗦一句：其实学习本来就不是易事，我写这篇文章的初衷也是希望大家学习起来更加轻松，充满乐趣。但是千万！千万不要把这篇文章收藏起来，或是存下地址，心里想着：以后有时间再看。这样的例子太多了，也许几年后你都没有再打开这个页面。无论如何，耐下心，读下去。这篇文章要比读课本要轻松、开心得多…… p.s.本文无论是cos还是sin，都统一用“正弦波”（Sine Wave）一词来代表简谐波。 一、什么是频域 从我们出生，我们看到的世界都以时间贯穿，股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为，世间万物都在随着时间不停的改变，并且永远不会静止下来。但如果我告诉你，用另一种方法来观察世界的话，你会发现世界是永恒不变的，你会不会觉得我疯了？我没有疯，这个静止的世界就叫做频域。 先举一个公式上并非很恰当，但意义上再贴切不过的例子： 在你的理解中，一段音乐是什么呢？

实验一 离散时间信号与系统的傅里叶分析

电子信息工程系实验报告 课程名称： 数字信号处理 实验项目名称：实验1 离散时间信号与系统的傅里叶分析 时间： 2012-3-17 班级：电信092 姓名：XXX 学号：910706201 实 验 目 的: 用傅里叶变换对离散时间信号和系统进行频域分析。 实 验 环 境: 计算机、MATLAB 软件 实 验 原 理： 对信号进行频域分析即对信号进行傅里叶变换。对系统进行频域分析即对其单位脉冲响应进行傅里叶变 换，得到系统的传输函数；也可由差分方程经过傅里叶变换直接求其传输函数，传输函数代表的就是频率响应特性。而传输函数是w 的连续函数，计算机只能计算出有限个离散频率点的传输函数值，故可在0～2∏之间取许多点，计算这些点的传输函数的值，并取它们的包络，所得包络即所需的频率特性。 实 验 内 容 和 步 骤: 1、已知系统用下面差分方程描述：y (n )=x (n )+ay (n -1)，试在a =0.95和a =0.5 两种情况下用傅立叶变换分析系统的频率特性。要求写出系统的传输函数，并打印|H (e j ω)|~ω曲线。 解：B=1;A=[1,-0.95]; [H,w]=freqz(B,A,'whole'); subplot(1,3,1);plot(w/pi,abs(H),'linewidth',2);grid on; xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|');title('幅频响应特性'); axis([0,2,0,2.5]); B=1;A=[1,-0.5];[H,w]=freqz(B,A,'whole'); subplot(1,3,3);plot(w/pi,abs(H),'linewidth',2);grid on; xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|');title('幅频响应特性'); axis([0,2,0,2.5]); 图形如下图1、2所示： 图1 a=0.95时的幅频响应特性 图2 a=0.5时的幅频响应特性 2、已知两系统分别用下面差分方程描述: y 1(n )=x (n )+x (n -1) y 2(n )=x (n )-x (n -1) 试分别写出它们的传输函数，并分别打印|H (e j ω)| ~ω曲线。 解：B=[1,1];A=1;[H,w]=freqz(B,A,'whole'); subplot(1,2,1);plot(w/pi,abs(H),'linewidth',2);grid on; 成 绩： 指导教师（签名）：

将下列各周期函数展开成傅里叶级数(下面给出函数在一个...

习题11-8 1. 将下列各周期函数展开成傅里叶级数(下面给出函数在一个周期内的表达式): (1))2 12 1(1)(2<≤--=x x x f ; 解 因为f (x )=1-x 2为偶函数, 所以b n =0(n =1, 2, ? ? ?), 而 611)1(4)1(2/1221 0221 020=-=-=??dx x dx x a , ?-=21022/1c o s )1(2/12dx x n x a n π 2 2 121 2 )1(2c o s )1(4π πn x d x n x n +-= -=? (n =1, 2, ? ? ?), 由于f (x )在(-∞, +∞)内连续, 所以 ∑ ∞ =+-+=1 2 1 2 2c o s )1(1 1211)(n n x n n x f ππ , x ∈(-∞, +∞). (2)?? ? ???? <≤-<≤<≤-=1 21 12 1 0 101 )(x x x x x f ; 解 2 1)(1 2 121 1 11 -=-+==????--dx dx xdx dx x f a n , ?? ??-+==--1 2 121 1 11 c o s c o s c o s c o s )(x d x n x d x n x d x n x x d x n x f a n ππππ 2 s i n 2])1(1[122πππ n n n n +--= (n =1, 2, ? ? ?), dx x n xdx n xdx n x xdx n x f b n ?? ??-+==--1 2 1210 1 1 1 sin sin sin sin )(ππππ π ππ n n n 12 c o s 2+-= (n =1, 2, ? ? ?).

傅里叶分析实验报告

班级: 姓名: 学号: 实验日期: 一、实验名称脉搏、语音及图像信号的傅里叶分析 二、实验目的 1、了解常用周期信号的傅里叶级数表示。 2、了解周期脉搏信号、语音信号及图像信号的傅里叶分析过程 3、理解体会傅里叶分析的理论及现实意义 三、实验仪器 脉搏语音实验仪器，数字信号发生器，示波器 四、实验原理 1、周期信号傅里叶分析的数学基础 任意一个周期为T 的函数f(t)都可以表示为傅里叶级数： 0001 0000000001()(cos sin )21()()1()cos()() 1()sin()()n n n n n f t a a n t b n t a f t d t a f t n t d t b f t n t d t ππ πππ πωωωωπωωωπωωωπ∞=---=++== =∑??? 其中0ω为角频率，称为基频，0a 为常数，n a 和n b 称为第n 次谐波的幅 值。任何周期性非简谐交变信号均可用上述傅里叶级数进行展开，即分解为一系列不同次谐波的叠加。 对于如图1所示的方波，一个周期内的函数表达式为: (0t<)2() (-t 0)2h f t h ππ?≤??=??-≤

其傅里叶级数展开为： 0100041()()sin(21)21411(sin sin 3 sin 5)35n h f t n t n h t t t ωπωωωπ∞==--=+++∑L 同理：对于如图2所示的三角波，函数表达式为： 4t (-t<)44()232(1) (t )44h T T f t t T T h T π?≤??=??-≤

傅里叶级数通俗解析

傅里叶级数 本文意在阐述傅里叶级数是什么，如何通过数学推导得出，以及傅里叶级数代表的物理含义。 1.完备正交函数集 要讨论傅里叶级数首先得讨论正交函数集。如果n个函数 φ1t,φ2t,…,φn t构成一个函数集，若这些函数在区间t1,t2上满足 φi tφj t t2 t1dt= 0 ,i≠j K i ,i=j(1) 如果是复数集，那么正交条件是 φi tφj?t t2 t1dt= 0 ,i≠j K i ,i=j(2) φj?t为函数φj t的共轭复函数。 有这个定义，我们可以证明出一些函数集是完备正交函数集。比如三角函数集和复指数函数集在一个周期内是完备正交函数集。 先证明三角函数集： 设φn t=cos nωt，φm t=cos mωt,把φn t，φm t代入(1)得 φi tφj t t0+T t0dt=cos nωt cos mωt dt t0+T t0 当n≠m时 =1 2 cos n+mωt+cos n?mωt t0+T t0 dt =1 2sin n+mωt (n+m)ω +sin n?mωt (n?m)ωt t0+T =0 (n,m=1,2,3,…,n≠m) 当n=m时 =1 2 cos2nωt t0+T t0 dt =T 2 再证两个都是正弦的情况 设φn t=sin nωt，φm t=sin mωt,把φn t，φm t代入(1)得 φi tφj t t0+T t0dt=sin nωt sin mωt dt t0+T t0 当n≠m时

=1 2 cos n+mωt?cos n?mωt t0+T t0 dt =1 2sin n+mωt (n+m)ω ?sin n?mωt (n?m)ωt t0+T =0 (n,m=1,2,3,…,n≠m) 当n=m时 =1 2 cos2nωt t0+T t0 dt =T 2 最后证明两个是不同名的三角函数的情况 设φn t=cos nωt，φm t=sin mωt,把φn t，φm t代入(1)得 φi tφj t t0+T t0dt=cos nωt sin mωt dt t0+T t0 =1 2 sin n+mωt?sin n?mωt t0+T t0 dt =1 2 ?cos n+mωt (n+m)ω +cos n?mωt (n?m)ωt t0+T =0 (n,m为任意整数) 因为两个三角函数相乘只有以上三种情况：两个皆为余弦函数相乘；两个皆为正弦函数相乘；一个为正弦函数，另一个为余弦函数相乘；三种情况皆满足正交函数集的定义，所以三角函数集为正交函数集。至于三角函数集的完备性可以从n，m的取值为任意整数可以得出，三角函数集是完备正交函数集。证毕。 由于三角函数集是完备正交函数集，而根据欧拉公式，我们容易联想到复指数函数集是否也是完备正交函数集呢。 接着是复指数函数集的证明 设φn t=?jnωt，φm t=?jmωt,则φj?t=??jmωt把φn t，φj?t代入(2)得 φi tφj?t t0+T t0dt=?jnωt t0+T t0 ??jmωt dt =?j(n?m)ωt t0+T t0 dt 当n≠m时，根据欧拉公式 =cos n?mωt+j sin?(n?m)ωt t0+T t0 dt =sin n?mωt n?mω?j cos?(n?m)ωt n?mωt t0+T =0 (n,m=1,2,3,…,n≠m)

傅里叶变换分析信号的缺点

傅里叶变换分析信号的缺点 基于傅里叶(Fourier)变换的信号频域表示,揭示了时间函数和频谱函数之间的内在联系,在传统的平稳信号分析和处理中发挥了极其重要的作用,很多理论研究和应用研究都把傅里叶变换当作最基本的经典工具来使用.但是傅里叶变换存在着严重的缺点:用傅里叶变换的方法提取信号频谱时,需要利用信号的全部时域信息,这是一种整体变换,缺少时域定位功能,因此必须对其加以改进. 傅里叶变换的特点及其局限性 设函数f(t)在(-,+)内有定义,且使广义积分 都收敛,则称(1)式定义的广义积分为函数f(t)的傅里叶变换,记为F{f(t)},(2)式定义的广义积分为逆傅里叶变换,记为{F()}。傅里叶变换可以完成从时域到频域的转换(正变换),也可以完成从频域到时域的转换(逆变换),但不能同时具有时域和频域信息。其核函数是,由于三角函数具有填满整个空间的特性,其在物理空间中是双向无限延伸的正弦波,在积分变换中体现为积分范围从+到-。因此,傅里叶变换是先天的非局限性,它对信号f(t)中体现任何局部信息处理都是相同的。而事实上,工程技术中的许多信号,如:语音信号、地震信号、心电图和各种电脉冲,他们的信号值只出现在一个短暂的时间间隔t内,以后快速减为零,t以外是未知的,可能为零,也可能是背景噪音,如果

用(1)式从信号中提取谱信号F(),就要取无限的时间量,使用过去的及将来的信号只为计算单个频谱,不能反映出随时间变化的频率,实际上我们需要的是确定的某个时间间隔内的频谱。这就使人们想到改进傅里叶变换使其能用来处理某个确定时间范围内的信号。Gabor提出的窗口傅里叶变换就是一个有效的方法。 另外,傅里叶变换之所得到广泛应用与透镜能实现傅里叶变换是分不开的。由公式 其中物平面为(,),焦平面为(),d0为物距,d1为象平面。要使=F{(,)},即准确实现傅里叶光学变换,只有在==f 时才能实现,否则将出现位相弯曲。并且,只有正透镜才能实现傅里叶变换,这些限制给工程技术中无疑增加了困难。这使得人们不得不寻求新得的方法,分数傅立叶变换不要求严频谱面,可根据需要在既包含空域信息也包括空频域信息的平面上进行处理,这使光学信息处理更具灵活性。 1傅里叶变换缺乏时间和频率的定位功能 傅里叶变换及其逆变换表示如下

深入浅出的讲解傅里叶变换

深入浅出的讲解傅里叶变换 我保证这篇文章和你以前看过的所有文章都不同，这是12年还在果壳的时候写的，但是当时没有来得及写完就出国了……于是拖了两年，嗯，我是拖延症患者…… 这篇文章的核心思想就是： 要让读者在不看任何数学公式的情况下理解傅里叶分析。 傅里叶分析不仅仅是一个数学工具，更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是，傅里叶分析的公式看起来太复杂了，所以很多大一新生上来就懵圈并从此对它深恶痛绝。老实说，这么有意思的东西居然成了大学里的杀手课程，不得不归咎于编教材的人实在是太严肃了。（您把教材写得好玩一点会死吗？会死吗？）所以我一直想写一个有意思的文章来解释傅里叶分析，有可能的话高中生都能看懂的那种。所以，不管读到这里的您从事何种工作，我保证您都能看懂，并且一定将体会到通过傅里叶分析看到世界另一个样子时的快感。至于对于已经有一定基础的朋友，也希望不要看到会的地方就急忙往后翻，仔细读一定会有新的发现。 ————以上是定场诗———— 下面进入正题： 抱歉，还是要啰嗦一句：其实学习本来就不是易事，我写这篇文章的初衷也是希望大家学习起来更加轻松，充满乐趣。但是千万！千万不要把这篇文章收藏起来，或是存下地址，心里想着：以后有时间再看。这样的例子太多了，也许几年后你都没有再打开这个页面。无论如何，耐下心，读下去。这篇文章要比读课本要轻松、开心得多…… 一、嘛叫频域 从我们出生，我们看到的世界都以时间贯穿，股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为，世间万物都在随着时间不停的改变，并且永远不会静止下来。但如果我告诉你，用另一种方法来观察世界的话，你会发现世界是永恒不变的，你会不会觉得我疯了？我没有疯，这个静止的世界就叫做频域。 先举一个公式上并非很恰当，但意义上再贴切不过的例子： 在你的理解中，一段音乐是什么呢？

傅里叶级数的三角形式和傅里叶级数的指数形式

周期信号的傅里叶级数分析 连续时间LTI 系统的时域分析: 以冲激函数为基本信号 系统零状态响应为输入信号与系统冲激响应之卷积 傅立叶分析 以正弦函数或复指数函数作为基本信号 系统零状态响应可表示为一组不同频率的正弦函数或复指数函数信号响应的加权和或积分; 周期信号: 定义在区间 (,)-∞∞ ，每隔一定时间 T ，按相同 规律重复变化的信号，如图所示 。它可表示为 f (t )=f ( t +m T ) 其中 m 为正整数， T 称为信号的周期，周期的倒数称为频率。 t ()t f 1 1 -T 2 /T 0 周期信号的特点： （1） 它是一个无穷无尽变化的信号，从理论上也是无始无终的，时 间范围为(,)-∞∞ （2） 如果将周期信号第一个周期内的函数写成 ，则周期信 号 ()f t 可以写成

0()() n f t f t nT ∞ =-∞ = -∑ （3）周期信号在任意一个周期内的积分保持不变，即有 ()()()a T b T T a b f t dt f t dt f t dt ++= =? ? ? 1. 三角形式的傅立叶级数 周期信号 f t () ，周期为1T ，角频率 11122T f π πω= = 该信号可以展开为下式三角形式的傅立叶级数。 []∑∞ =++ =++++++++=1 1 1 011121211110)sin()cos(...)sin()cos(... )2sin()2cos()sin()cos()(n n n n n t n b t n a a t n b t n a t b t a t b t a a t f ωωωωωωωω 式中各正、余弦函数的系数 n n b a , 称为傅立叶系数,函数通过它可以完全表示。 傅立叶系数公式如下

周期性函数分解的傅里叶级数

周期性函数分解的傅里叶级数 周期电压、电流等都可以用一个周期函数表示，即 210),()(、、 =+=k kt t f t f 式中T 是周期函数的周期，且 210、、 =k 如果给定的周期函数在有限的区间内，只有有限个第一类间断点和有限个极大值和极小值，那么就可以展开成一个收敛的级数（三角级数） 设给定的周期函数)(t f ，则)(t f 可展开成 ） （）（1)sin cos (sin cos )2sin 2cos ()sin cos ()(1022110 ∑∞ =++=+++++++=k k k k k t k b t k a a t k b t k a t b t a t b t a a t f ωωωωωωωω 上式中的系数，可按下列公式计算： ????? ?? ? - - -= ====== = π ππ π ππωωπ ωωπωωωπ ωωπω) (sin )(1 ) (sin )(1sin )(2)(cos )(1 ) (cos )(1cos )(2)(1 )(1 20 020 00 22 0t td k t f t td k t f tdt k t f T b t td k t f t td k t f tdt k t f T a dt t f T dt t f T a T k T k T T T ）（2 这些公式的对导，主要的依据是利用三角函数的定积分的特点。 设m.n 是任意整数，则下列定积分成立： ?=π 200 sin mxdx ? =π 20 cos mxdx ?=π 200cos sin nxdx mx ， n m ≠ ?=π 200 sin sin nxdx mx , n m ≠ ? =π 200cos cos nxdx mx , n m ≠ ? =π π 20 2)(sin dx mx ,

深入浅出的讲解傅里叶变换(2)

深入浅出的讲解傅里叶变换(2) 上一篇文章发出来之后，为了掐死我，大家真是很下工夫啊，有拿给姐姐看的，有拿给妹妹看的，还有拿给女朋友看的，就是为了听到一句“完全看不懂啊”。幸亏我留了个心眼，不然就真的像标题配图那样了。我的文章题目是，如果看了这篇文章你“还”不懂就过来掐死我，潜台词就是在你学了，但是没学明白的情况下看了还是不懂，才过来掐死我。 另外，想跟很多人抱歉，因为评论太多了，时间有限，不能给每个人回复，还望大家谅解。但是很感谢一直在评论区帮忙解答读者问题的各位，就不一一@了。 这里郑重感谢大连海事大学的吴楠老师，一位学识渊博、备课缜密、但授课不拘一格的年轻教师！当时大三他教我通信原理，但是他先用了4结课帮我们复习了很多信号与系统的基本概念，那个用乐谱代表频域的概念就是他讲的，一下子让我对这门课豁然开朗，才有了今天的这篇文章。 ————————————今天的定场诗有点长—————————— 下面继续开始我们无节操的旅程： 上次的关键词是：从侧面看。这次的关键词是：从下面看。 在第二课最开始，我想先回答很多人的一个问题：傅里叶分析究竟是干什么用的？这段相对比较枯燥，已经知道了的同学可以直接跳到下一个分割线。 先说一个最直接的用途。无论听广播还是看电视，我们一定对一个词不陌生——频道。频道频道，就是频率的通道，不同的频道就是将不同的频率作为一个通道来进行信息传输。下面大家尝试一件事： 先在纸上画一个sin（x），不一定标准，意思差不多就行。不是很难吧。 好，接下去画一个sin（3x）+sin（5x）的图形。 别说标准不标准了，曲线什么时候上升什么时候下降你都不一定画的对吧？ 好，画不出来不要紧，我把sin（3x）+sin（5x）的曲线给你，但是前提是你不知道这个曲线的方程式，现在需要你把sin（5x）给我从图里拿出去，看看剩下的是什么。这基本是不可能做到的。 但是在频域呢？则简单的很，无非就是几条竖线而已。

对傅里叶分析的新颖理解

这篇文章的核心思想就是：要让读者在不看任何数学公式的情况下理解傅里叶分析。 傅里叶分析不仅仅是一个数学工具，更是一种可以彻底颠覆一个人以前世界观的思维模式。 一、嘛叫频域 关键词：从侧面看 从我们出生，我们看到的世界都以时间贯穿，股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为，世间万物都在随着时间不停的改变，并且永远不会静止下来。但如果我告诉你，用另一种方法来观察世界的话，你会发现世界是永恒不变的，你会不会觉得我疯了？我没有疯，这个静止的世界就叫做频域。 先举一个公式上并非很恰当，但意义上再贴切不过的例子：在你的理解中，一段音乐是什么呢？ 这是我们对音乐最普遍的理解，一个随着时间变化的震动。但我相信对于乐器小能手们来说，音乐更直观的理解是这样的： 上图是音乐在时域的样子，而下图则是音乐在频域的样子。所以频域这一概念对大家都从不陌生，只是从来没意识到而已。 现在我们可以回过头来重新看看一开始那句痴人说梦般的话：世界是永恒的。 将以上两图简化： 时域： 频域： 在时域，我们观察到钢琴的琴弦一会上一会下的摆动，就如同一支股票的走势；而在频域，只有那一个永恒的音符。 你眼中看似落叶纷飞变化无常的世界，实际只是躺在上帝怀中一份早已谱好的乐章。

傅里叶同学告诉我们，任何周期函数，都可以看作是不同振幅，不同相位正/余弦波的叠加。在第一个例子里我们可以理解为，利用对不同琴键不同力度，不同时间点的敲击，可以组合出任何一首乐曲。 而贯穿时域与频域的方法之一，就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数（Fourier Serie）和傅里叶变换(Fourier Transformation)，我们从简单的开始谈起。 二、傅里叶级数(Fourier Series) 如果说能用余弦曲线波叠加出一个带90度角的矩形波来，你会相信吗？但是看看下图： 第一幅图是一个郁闷的余弦波cos（x） 第二幅图是2个卖萌的余弦波的叠加cos(x)+a cos(3x) 第三幅图是4个发春的余弦波的叠加 第四幅图是10个便秘的余弦波的叠加 随着余弦波数量逐渐的增长，他们最终会叠加成一个标准的矩形，大家从中体会到了什么道理？ 随着叠加的递增，所有余弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡，而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个余弦波叠加起来才能形成一个标准90度角的矩形波呢？不幸的告诉大家，答案是无穷多个。 不仅仅是矩形，你能想到的任何波形都是可以如此方法用正/余弦波叠加起来的。 这是没有接触过傅里叶分析的人在直觉上的第一个难点，但是一旦接受了这样的设定，游戏就开始有意思起来了。 还是上图的余弦波累加成矩形波，我们换一个角度来看看：

脉搏、语音及图像信号的傅里叶分析

脉搏、语音及图像信号的傅里叶分析 一、实验目的 1、了解常用周期信号的傅里叶级数表示。 2、了解周期脉搏信号、语音信号及图像信号的傅里叶分析过程 3、理解体会傅里叶分析的理论及现实意义 二、实验原理 任意一个周期为T 的函数f(t)都可以表示为傅里叶级数： 0001 0000000001()(cos sin )21()()1()cos()()1()sin()()n n n n n f t a a n t b n t a f t d t a f t n t d t b f t n t d t ππ π πππωωωωπωωωπωωωπ∞=---=++== =∑??? 其中0ω为角频率，称为基频，0a 为常数，n a 和n b 称为第n 次谐波的幅值。任何周期性非简谐交变信号均可用上述傅里叶级数进行展开，即分解为一系列不同次谐波的叠加。 对于如图1所示的方波，一个周期内的函数表达式为: (0t<)2() (-t 0)2h f t h ππ?≤??=??-≤

1202100022281()(1)()sin(21)21 811(sin sin 3sin 5) 35n n h f t n t n h t t t ωπωωωπ∞-==---=-++∑ 图1 方波 图2 三角波 从以上各式可知，任何周期信号都可以表示为无限多次谐波的叠加，谐波次数越高，振幅越小，它对叠加波的贡献就越小，当小至一定程度时(谐波振幅小于基波振幅的5%)，则高次的谐波就可以忽略而变成有限次数谐波的叠加，这对设计仪器电路是很有意义的。 三、实验仪器 脉搏语音实验仪器，数字信号发生器，示波器 四、实验内容 1.傅里叶级数的合成 （1）利用数字信号发生器产生频率分别为100Hz 、300Hz 、500Hz 的正弦信号，并使其位相相同，振幅比为：1:1/3: 1/5,将上述三个信号，分别通过加法器输入到傅里叶分析仪，观察并记录其波形。 （2）利用数字信号发生器产生方波，输入到傅里叶分析仪，并将其与上述合成后的信号相比较。两者有何差异？试分析引起的原因，应如何消除？ （3）利用数字信号发生器产生频率分别为200Hz 、600Hz 、1000Hz 的正弦信号,振幅比为：1:1/32:1/52，并且保证其相位相差180°，然后通过加法器输入到傅里叶分析仪，观察并记录其波形，并与数字信号发生器产生的三角波相比较。 （4）利用傅里叶分析仪分别产生方波与三角波，进行傅里叶分析，记录各正弦波频率以及相对的幅度之间的关系，并与上述加法器输入信号相比较。 2.滤波与选频分析 对上述（4）傅里叶分析的频谱，分别选择低频段和高频段信号通过傅里叶反变换，观察它们图像并导出保存，试分析低通滤波和高通滤波图像的区别。 3.周期信号傅里叶分析的应用： （1）“脉搏信号”的傅里叶分析 1）用傅里叶分析仪软件中提供的“脉搏信号”模块和压电晶体测试自己脉搏波的信号，观察你的脉搏信号。

第三章傅里叶变换分析.doc

第三章 傅里叶变换分析 1．什么是频谱？如何得到信号的频谱？ 目前我们熟悉的是信号幅度随着时间变化而变化的常见表示方式，比如正弦信号的幅度随着时间按正弦函数的规律变化；另一方面，对于正弦信号，如果知道其振幅、频率和相位，则正弦信号的波形也惟一确定。根据这个原理和傅里叶级数理论，满足一定条件的周期信号都可以分解为不同频率的正弦分量的线性组合，从而我们用各个正弦分量的频率-幅度、频率-相位来表示周期信号的描述方式就称为周期信号的频谱表示，随着对信号研究的深入，我们将周期信号的频谱表示又推广到非周期信号的频谱表示，即通常的傅里叶变换。 对于周期信号，其频谱一般用傅里叶级数表示，而傅里叶级数的系数就称为信号的频谱： ()0110111()cos sin cos()T n n n n n n f t a a n t b n t c c n t ωωω?∞∞ ===++=++∑∑ 或 1()jn t T n n f t F e ω∞=-∞= ∑ 其中： 122 00 1() 0,1,2,...,1() 1,2, (2) T jn t T n T n n n F f t e dt n T F a jb n F a ω--==±±±∞=-=∞=? 对于非周期信号，其频谱一般用傅里叶变换表示： 1 ()()2j t f t F j e d ωωωπ ∞-∞=? 其中： ()() j t F j f t e dt ωω∞--∞=? 2．周期信号和非周期信号的频谱有何不同？ 周期信号的频谱可以用傅里叶级数表示，它是离散的、非周期的和收敛的。 而非周期信号的频谱用傅里叶变换表示，它是连续的、非周期的和收敛的。若假设周期信 号为()T f t ， 非周期信号为0() ()220 otherwise T T T f t t f t ?-<≤?=???，并假设周期信号()T f t 的傅里叶级数 的系数为n F ，非周期信号0()f t 的傅里叶变换为()F j ω，则有如下的关系：

傅里叶变换本质及其公式解析

傅里叶变换的本质 傅里叶变换的公式为 dt e t f F t j ? +∞ ∞--=ωω)()( 可以把傅里叶变换也成另外一种形式： t j e t f F ωπω),(21 )(= 可以看出，傅里叶变换的本质是内积，三角函数是完备的正交函数集，不同频率的三角函数的之间的内积为0，只有频率相等的三角函数做内积时，才不为0。 )(2,21)(2121Ω-Ω==?Ω-ΩΩΩπδdt e e e t j t j t j 下面从公式解释下傅里叶变换的意义 因为傅里叶变换的本质是内积，所以f(t)和t j e ω求内积的时候，只有f(t)中频率为ω的分量才会有内积的结果，其余分量的内积为0。可以理解为f(t)在t j e ω上的投影，积分值是时间从负无穷到正无穷的积分，就是把信号每个时间在ω的分量叠加起来，可以理解为f(t)在t j e ω上的投影的叠加，叠加的结果就是频率为ω的分量，也就形成了频谱。 傅里叶逆变换的公式为 ωωπωd e F t f t j ?+∞∞-=)(21 )( 下面从公式分析下傅里叶逆变换的意义 傅里叶逆变换就是傅里叶变换的逆过程，在)(ωF 和t j e ω-求内积的时候，)(ωF 只有t 时刻的分量内积才会有结果，其余时间分量内积结果为0，同样积分值是频率从负无穷到正无穷的积分，就是把信号在每个频率在t 时刻上的分量叠加起来，叠加的结果就是f(t)在t 时刻的值，这就回到了我们观察信号最初的时域。 对一个信号做傅里叶变换，然后直接做逆变换，这样做是没有意义的，在傅里叶变换和傅里叶逆变换之间有一个滤波的过程。将不要的频率分量给滤除掉，然后再做逆变换，就得到了想要的信号。比如信号中掺杂着噪声信号，可以通过滤波器将噪声信号的频率给去除，再做傅里叶逆变换，就得到了没有噪声的信号。 优点：频率的定位很好，通过对信号的频率分辨率很好，可以清晰的得到信号所包含的频率成分，也就是频谱。 缺点：因为频谱是时间从负无穷到正无穷的叠加，所以，知道某一频率，不能判断，该频率的时间定位。不能判断某一时间段的频率成分。 例子： 平稳信号：x(t)=cos(2*pi*5*t)+cos(2*pi*10*t)+cos(2*pi*20*t)+cos(2*pi*50*t)

典型信号的傅里叶变换

例9.1 试将图9.3中所示的非正弦周期信号（称为方波信号）展成傅里叶级数。 解 根据图上所示信号的波形，可知其既对称于纵轴，又具有半波对称性质，所以它是兼有奇谐波函数性质的偶函数。依照上述定理，此信号的傅里叶级数中必定只含有余弦的奇次谐波项，因此只需按公式 ()2 04cos T km A f t k tdt T ω= ? 计算A km 。 对图上的波形图可以写出 ()04 42 T A t f t T T A t ?

故有 4044444sin 2sin T T km T A A B t k tdt t A k tdt T T T T ωω?? = -- ??? ?? 参照积分公式 211 sin sin cos x axdx ax x ax a a = -? 可算出 22 22 81,5,9,83,7,11km A k k B A k k ππ?=??=? ?-=? ? 于是所欲求的傅里叶级数 ()2222 8111 sin sin 3sin 5sin 7357 A f t t t t t ωωωωπ?? = -+-+ ??? 。 例9.3 已知一如图9.5所示的信号波形，试求其傅里叶级数。 图9.5 例9.3用图 解 此信号对原点对称，是奇函数，且又是半波横轴对称，所以其傅里叶级数仅是正弦奇次谐波分量组成。由于 ()022 T A t f t T A t T ?

傅里叶级数的数学推导解析

傅里叶级数的数学推导 首先，隆重推出傅里叶级数的公式，不过这个东西属于“文物”级别的，诞生于19世纪初，因为傅里叶他老人家生于1768年，死于1830年。 但傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用，这不由得让人肃然起敬。一打开《信号与系统》、《锁相环原理》等书籍，动不动就跳出一个“傅里叶级数”或“傅里叶变换”，弄一长串公式，让人云山雾罩。 如下就是傅里叶级数的公式： 不客气地说，这个公式可以说是像“臭婆娘的裹脚布——又臭又长”，而且来历相当蹊跷，不知那个傅里叶什么时候灵光乍现，把一个周期函数f(t硬生生地写成这么一大堆东西。单看那个①式，就是把周期函数f(t描述成一个常数系数a0、及1倍ω的sin和cos函数、2倍ω的sin和cos函数等、到n倍ω的sin和cos函数等一系列式子的和，且每项都有不同的系数，即An和Bn，至于这些系数，需要用积分来解得，即②③④式，不过为了积分方便，积分区间一般设为[-π, π]，也相当一个周期T的宽度。 能否从数学的角度推导出此公式，以使傅里叶级数来得明白些，让我等能了解它的前世今生呢？下面来详细解释一下此公式的得出过程： １、把一个周期函数表示成三角级数：

首先，周期函数是客观世界中周期运动的数学表述，如物体挂在弹簧上作简谐振动、单摆振动、无线电电子振荡器的电子振荡等，大多可以表述为： f(x=A sin(ωt+ψ 这里t表示时间，A表示振幅，ω为角频率，ψ为初相（与考察时设置原点位置有关）。 然而，世界上许多周期信号并非正弦函数那么简单，如方波、三角波等。傅叶里就想，能否用一系列的三角函数An sin(nωt+ψ之和来表示那个较复杂的周期函数f(t呢？因为正弦函数sin可以说是最简单的周期函数了。于是，傅里叶写出下式：（关于傅里叶推导纯属猜想） 这里，t是变量，其他都是常数。与上面最简单的正弦周期函数相比，5式中多了一个n，且n从1到无穷大。这里f(t是已知函数，也就是需要分解的原周期函数。从公式5来看，傅里叶是想把一个周期函数表示成许多正弦函数的线性叠加，这许许多多的正弦函数有着不同的幅度分量（即式中An）、有不同的周期或说是频率（是原周期函数的整数倍，即n）、有不同的初相角（即ψ），当然还有一项常数项（即A0）。要命的是，这个n是从1到无穷大，也就是是一个无穷级数。 应该说，傅里叶是一个天才，想得那么复杂。一般人不太会把一个简单的周期函数弄成这么一个复杂的表示式。但傅里叶认为，式子右边一大堆的函数，其实都是最简单的正弦函数，有利于后续的分析和计算。当然，这个式能否成立，关键是级数中的每一项都有一个未知系数，如A0、An等，如果能把这些系数求出来，那么5式就可以成立。当然在5式中，唯一已知的就是原周期函数f(t,那么只需用已知函数f(t来表达出各项系数，上式就可以成立，也能计算了。 于是乎，傅里叶首先对式5作如下变形： 这样，公式５就可以写成如下公式６的形式：

傅里叶级数

傅里叶级数（Fourier Series ） 引言 正弦函数是一种常见而简单的周期函数，例如描述简谐振动的函数 就是一个以ωπ 2为周期的函数。其中y 表示动点的位置，t 表示时间，A 为振幅，ω为 角频率，?为初相。 但在实际问题中，除了正弦函数外，还会遇到非正弦的周期函数，它们反映了较复杂的周期运动，我们也想将这些周期函数展开成由简单的周期函数例如三角函数组成的级数。具体地说，将周期为)2(ωπ =T 的周期函数用一系列以T 为周期的正弦函数 )sin(n n t n A ?ω+组成的级数来表示，记为 其中),3,2,1(,,0Λ=n A A n n ?都是常数。 将周期函数按上述方式展开，它的物理意义就是把一个比较复杂的周期运动看成是许多不同频率的简谐振动的叠加。在电工学上，这种展开称为谐波分析。其中常数项0A 称为 )(t f 的直流分量；)sin(11?ω+t A 称为一次谐波（又叫做基波） ；而)2sin(22?ω+t A ， Λ)3sin(33?ω+t A 依次称为二次谐波，三次谐波，等等。 为了下面讨论方便起见，我们将正弦函数)sin(n n t n A ?ω+按三角公式变形，得 t n A t n A t n A n n n n n n ω?ω??ωsin cos cos sin )sin(+=+， 令x t A b A a A a n n n n n n ====ω??,cos ,sin ,2 00，则上式等号右端的级数就可以改写成 这个式子就称为周期函数的傅里叶级数。 1.函数能展开成傅里叶级数的条件 （1） 函数)(x f 须为周期函数； （2） 在一个周期内连续或只有有限个第一类间断点；（如果0x 是函数)(x f 的间断点，但 左极限)0(0-x f 及右极限)0(0+x f 都存在，那么0x 称为函数)(x f 的第一类间断点） （3） 在一个周期内至多只有有限个极值点。