奥数几何的五大模型问题

奥数几何的五大模型问题
例题1:图17是一个正方形地板砖示意图,在大正方形ABCD中
AA1=AA2=BB1=BB2=CC1=CC2=DD1=DD2,中间小正方形 EFGH的面积是16平方厘米,四块蓝色的三角形的面积总和是72平方厘米,那么大正方形ABCD的面积是多少平方厘米?
分析与解连AC和BD两条大正方形的对角线,它们相交于O,然后将三角形AOB放在DPC处(如图18和图19)。
已知小正方形EFGH的面积是16平方厘米,所以小正方形EFGH 的边长是4厘米。
又知道四个蓝色的三角形的面积总和是72平方厘米,所以两个蓝色三角形的面积是72÷2=36平方厘米,即图19的正方形OCPD中的小正方形的面积是36平方厘米,那么这个正方形的边长就是6厘米。由此得出,正方形OCPD的边长是4+6=10厘米,当然正方形OCPD 的面积就是102,即100平方厘米。而正方形OCPD的面积恰好是正方形ABCD的面积的一半,因此正方形ABCD的面积是200平方厘米。
答:正方形ABCD的面积是200平方厘米。
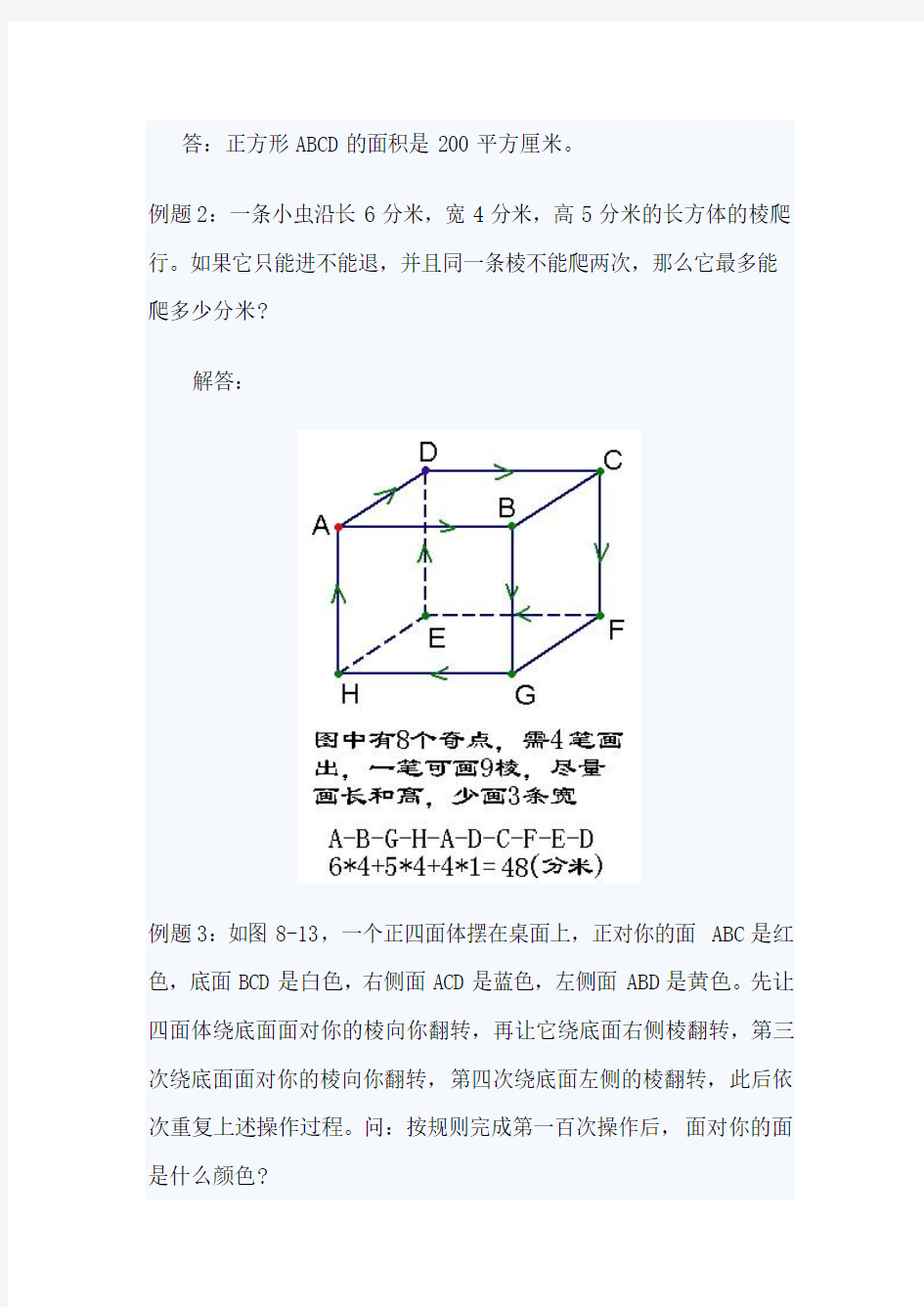
例题2:一条小虫沿长6分米,宽4分米,高5分米的长方体的棱爬行。如果它只能进不能退,并且同一条棱不能爬两次,那么它最多能爬多少分米?
解答:
例题3:如图8-13,一个正四面体摆在桌面上,正对你的面ABC是红色,底面BCD是白色,右侧面ACD是蓝色,左侧面ABD是黄色。先让四面体绕底面面对你的棱向你翻转,再让它绕底面右侧棱翻转,第三次绕底面面对你的棱向你翻转,第四次绕底面左侧的棱翻转,此后依次重复上述操作过程。问:按规则完成第一百次操作后,面对你的面是什么颜色?
解答:
例题4:有一个长方体木块,长125厘米,宽40厘米,高25厘米。把它锯成若干个体积相等的小正方体,然后再把这些小正方体拼成一个大正方体。这个大正体的表面积是多少平方厘米?
分析与解一般说来,要求正方体的表面积,一定要知道正方体的棱长。题中已知长方体的长、宽、高,同正方体的棱长又没有直接联系,这样就给解答带来了困难。我们应该从整体出发去思考这个问题。
按题意,这个长方体木块锯成若干个体积相等的小正方体后,又拼成一个大正方体。这个大正方体的体积和原来长方体的体积是相等的。已知长方体的长、宽、高,就可以求出长方体的体积,这就是拼成的大正方体的体积。进而可以求出正方体的棱长,从而可以求出正方体的表面积了。
长方体的体积是
125×40×25=125000(立方厘米)
将 125000分解质因数:
125000=2×2×2×5×5×5×5×5×5
=(2×5×5)×(2×5×5)×(2×5×5)
可见大正方体的棱长是
2×5×5=50(厘米)
大正方体的表面积是
50×50×6=15000(平方厘米)
答:这个大正方体的表面积是15000平方厘米。
例题6:有50个表面涂有红漆的正方体,它们的棱长分别是1厘米、3厘米、5厘米、7厘米、9厘米、……、99厘米,将这些正方体锯
成棱长为1厘米的小正方体,得到的小正方体中,至少有一个面是红色的小正方体共有多少个?
分析与解棱长为1厘米涂有红漆的小正方体,不用锯,就是棱长1厘米的小正方体,它当然是至少有一个面是红色的小正方体了。
将棱长为3厘米的涂有红漆的小正方体,锯成棱长为1厘米的小正方体,共得到33个,其中没有涂红漆的共(3-2)3个。
将棱长为5厘米的涂有红漆的小正方体锯成棱长为1厘米的小正方体,共得53个,其中没有涂红漆的共(5-2)3个。
将棱长为7厘米的涂有红漆的小正方体锯成棱长为1厘米的小正方体,共得73个,其中没有涂红漆的共(7-2)3个。
由以上分析、计算发现,将校长为1厘米、3厘米、5厘米、7厘米的四个正方体锯成棱长为1厘米的小正方体后,得到至少有一个面为红色的小正方体共有
13+33-(3-2)3+53-(5-2)3+73-(7-2)3
=13+33-13+53-33+73-53
=13+33+53+73-13-33-53=73=343(个)
按照这样的规律可得,将棱长为1厘米、3厘米、5厘米、7厘米、9厘米、……、99厘米这50个正方体锯成棱长为1厘米的小正方体后,得到至少有一个面为红色的小正方体共有:
13+33+53+73+93+……+973+993-13-33-53-73-93-……
-973=993=970299(个)
答:至少有一个面是红色的小正方体共有970299个。
例题7:为了美化校园,东升小学用鲜花围成了两个圆形花坛。小圆形花坛的面积是3.14平方米,大圆形花坛的半径是小圆形花坛半径的2倍。大圆形花坛的面积比小圆形花坛的面积大多少平方米?
分析与解我们知道圆的面积与半径的平方成正比。题中告诉我们,大圆的半径是小圆半径的2倍,那么大圆面积是小圆面积的22倍。
大圆形花坛的面积比小圆形花坛的面积大
3.14×(22-1)
=3.14×3
=9.42(平方米)
答:大圆形花坛的面积比小圆形花坛的面积大9.42平方米
例题8:图21是一个圆形钟面,圆周被平均分成了12等份。已知圆
形的半径是6厘米,那么图中阴影的面积是多少平方厘米?
分析与解题中告诉我们:圆周被平均分成了12等份,因此连接OE,
答:阴影的面积是18.84平方厘米。
小学奥数之几何五大模型精编版
一、等积变换模型 ⑴等底等高的两个三角形面积相等; 其它常见的面积相等的情况 ⑵两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比。 如上图12::S S a b = ⑶夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。 ⑷正方形的面积等于对角线长度平方的一半; ⑸三角形面积等于与它等底等高的平行四边形面积的一半; 五大模型 1S 2 S
二、鸟头定理(共角定理)模型 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。 如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =??△△ 图1 图2 三、蝴蝶定理模型 任意四边形中的比例关系(“蝴蝶定理”): ①1243::S S S S =或者1324S S S S ?=?②()()1243::AO OC S S S S =++ 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。 梯形中比例关系(“梯形蝴蝶定理”) ①2213::S S a b = ②221324::::::S S S S a b ab ab =; ③梯形S 的对应份数为()2 a b +。
小学奥数-几何五大模型(蝴蝶模型)整理版
任意四边形、梯形与相似模型 卜亠\ 模型三蝴蝶模型(任意四边形模型) 任意四边形中的比例关系(“蝴蝶定理”): D S1: S2 = S4: S3或者S S3 =S2 S4 ② AO : OC =[S S2 : S4 S3 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。 【例1】(小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD被对角线AC BD分成四个部分,△ AOB面积为1平方千米,△ BOC面积为2平方千米,△ COD勺面积为3平方千米,公园由陆地面积是 6. 92平方千米和人工湖组成,求人工湖的面积是多少平方千米? 【分析】根据蝴蝶定理求得S^AOD=3 1-'2=1.5平方千米,公园四边形ABCD的面积是12 3 45 = 7.5平方千米,所以人工湖的面积是7.5-6.92=0.58平方千米 【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知, 求:⑴三角形BGC的面积:⑵AG:GC= ? 【解析】⑴根据蝴蝶定理,S BGC 1=2 3,那么S BGC=6 ; ⑵根据蝴蝶定理,AG:G^ 1 2 : 3 6 =1:3 . (? ??) 【例2】四边形ABCD的对角线AC与BD交于点0(如图所示)。如果三角形ABD的面积等于三角形BCD的
面积的 1 ,且AO =2 , DO =3,那么CO的长度是DO的长度的_____________ 倍。 3 【解析】在本题中,四边形ABCD为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。看到题目中给出条件S A BD : S BCD =1:3,这可以向模型一蝴蝶定理靠拢,于是得出一种解法。又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形”,于是可以作AH垂直BD于H , CG垂直BD于G,面积比转化为高之比。再应用结论:三角形高相同,则面积之比等于底边之比,得出结果。请老师注意比较两种解法,使学生体会到蝴蝶定理的优势,从而主观上愿意掌握并使用蝴蝶定理解决问题。 解法一:T AO :OC = S ABD: S BDC =1 : 3 , 二OC =2 3 =6 , ??? OC:OD =6:3 2:1 . 解法二:作AH _BD 于H , CG_BD 于G . ?- AH」CG , 3 1 ?- AO CO , 3 ?OC =2 3=6 , ?OC:OD =6:3 =2:1 ? 【例3】如图,平行四边形ABCD的对角线交于O点,A CEF、△OEF、△ODF、△BOE的面积依次是2、 4、4和6。求:⑴求A OCF的面积;⑵求A GCE的面积。 【解析】⑴根据题意可知,△BCD的面积为2 4 4 ^16,那么△BCO和:CDO的面积都是16亠2=8 , 所以A OCF 的面积为8—4=4; ⑵由于△ BCO的面积为8, △BOE的面积为6,所以A OCE的面积为8-6=2 , 根据蝴蝶定理,EG:FG 二 Sg E:S.COF =2:4 =1:2,所以S.GCE:S.GCF = EG : FG =1:2 , 1 1 2 那么S GCE S CEF 2 ~~? 1+2 3 3 【例4】图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷。那么最大的一个三角形的面积是多少公顷? S 'ABD S BCD 3审 S AOD =—S DOC 3
小学奥数-几何五大模型(鸟头模型)-精选.
模型二 鸟头模型 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2), 则:():()ABC ADE S S AB AC AD AE =??△△ E D C B A E D C B A 图⑴ 图⑵ 【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =, 16ADE S =△平方厘米,求ABC △的面积. 三角形等高模型与鸟头模型
E D C B A E D C B A 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===??△△, ::4:7(45):(75) ABE ABC S S AE AC ===??△△,所以:(24):(75)ADE ABC S S =??△△,设 8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角 形ADE 的面积等于1,那么三角形ABC 的面积是多少? E D C B A A B C D E 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S =V V 又∵5AB AD = ∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V . 【巩固】如图,三角形被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =, 6AE =,乙部分面积是甲部分面积的几倍? 乙 甲 E D C B A A B C D E 甲 乙 【解析】 连接AD . ∵3BE =,6AE = ∴3AB BE =,3ABD BDE S S =V V 又∵4BD DC ==, ∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲.
小学奥数-几何五大模型(鸟头模型).
模型二鸟头模型 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在 △ABC中,D,E分别是AB,AC上的点如图(1)(或D在BA的延长线上,E在AC上如图2),则ABC : ADE -(AB AC): (AD AE) 厘米,求△ ABC的面积. 【解析】连接BE , S A ADE : S A ABE= AD : AB =2 :5 =(2 4): (5 4), S A ABE : S A ABC = AE : AC = 4 : 7 = (4 5) : (7 5),所以S^ADE: S^ ABC= (2 4) : (7 5),设S A ADE= 8 份, 则S A ABC =35份,S A ADE =16平方厘米,所以1份是2平方厘米,35份就是70平方厘米,△ ABC的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 三角形等高模型与鸟头模型 【例1】如图在△ ABC中, D,E分别是AB,AC上的点,且AD: AB =2:5 ,AE:AC =4:7 , S^ADE =16 平方 图⑵
【巩固】如图,三角形ABC中,AB是AD的5倍,AC是AE的 3 倍,如果三角形么三 角形ABC的面积是多少? ?/ EC =3AE --S A BC = 3S ABE 又??? AB =5AD --S|_ADE = S_ABE 5 = S_ ABC 15 ,??? S ABC 如图,三角形ABC被分成了甲(阴影部分)、乙两部分,BD=DC=4 , BE=3 , AE=6,乙部分面积是甲部分面积的几倍? ?/ BE =3 , AE =6 --AB = 3BE , S ABD=3S BDE 又T BD =DC =4 , --S ABC =2S ABD,…S ABC - 6S BDE , 【例2】如图在△ ABC中,D在BA的延长线上,E在AC上,且AB: AD =5: 2 , AE:EC=3:2 , S A ADE =12平方厘米,求△ ABC的面积. 【解析】连接BE , S A ADE : S A ABE= AD: AB =2:5 =(2 3): (5 3) S A ABE : S A ABC=AE: AC =3:(3 2)=(3 5): 1(3 2) 5】, 所以S A ADE : S A ABC - (3 2) : 5 (3 2^ - 6 : 25,设S A ADE = 6 份,贝V S A ABC = 25 份,S A ADE =12 平方厘 米,所以1份是2平方厘米,25份就是50平方厘米,△ ABC的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 【例3】如图所示,在平行四边形ABCD中,E为AB的中点,AF =2CF,三角形AFE(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米? ADE的面积等于1,那 = 15S ADE =15 . 【巩固】 【解析】连接AD . 【解 析】
六年级奥数专题几何五大模型鸟头模型
六年级奥数专题几何五大 模型鸟头模型 The latest revision on November 22, 2020
几何五大模型——鸟头模型 本讲要点 一两点都在边上:鸟头定理: (现出“鸟头模型”。然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。最后真实的鸟头隐去,只留下几何模型。最后按一下,出公式。) 二一点在边上,一点在边的延长线上:
例1 如图,AD=DB ,AE=EF=FC ,已知阴影部分面积为5平方厘米,△ABC的面积是平方厘米. 例2 例2 (1)如图在△ABC中,D、E分别是AB,AC上的点,且AD:AB=2:5, AE:AC=4:7,△ABC的面积是16平方厘米,求△ABC的面积。 (2)如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE 的面积是12平方厘米,求△ABC的面积。 例3 已知△DEF的面积为12平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC的面积。 例4 三角形ABC面积为1,AB边延长一倍到D,BC延长2倍到E,CA延长3倍到F,问三角形DEF的面积为多少 例5 长方形ABCD面积为120,EF为AD上的三等分点,G、H、I为DC上的四等分点,阴影面积是多大
如图,过平行四边形ABCD 内的一点P 作边AD 、BC 的平行线EF 、GH ,若PBD ?的面积为8平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米 1. 如下左图,在ABC △中,D 、E 分别是BC 、AB 的三等分点,且ABC △的面积是54,求 CDE △的面积。 2. 如图,长方形ABCD 的面积是1,M 是AD 边的中点,N 在AB 边上,且12AN BN =.那么,阴影部分的面积等 于 . 3. 如图以ABC △的三边分别向外做三个正方形ABIH 、ACFG 、BCED ,连接HG 、EF 、 ID ,又得到三个三角形,已知六边形DEFGHI 的面积是77平方厘米,三个正方形的面积分别是9、16、36平方厘米,则三角形ABC 的面积是多少 4. 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使 2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积。 5. 把四边形ABCD 的各边都延长2倍,得到一个新的四边形EFGH 。如果ABCD 的面积是5 平方厘米,则EFGH 的面积是多少 家庭作业 例6 A C E
几何五大模型汇总
小学平面几何五大模型 一、 共角定理 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E分别是, AB AC上的点如图⑴(或D在BA的延长线上,E在AC上),则:():() S S AB AC AD AE =?? △△ 证明:由三角形面积公式S=1/2*a*b*sinC可推导出 若△ABC和△ADE中, ∠BAC=∠DAE 或∠BAC+∠DAE=180°, 则 ADE ABC S S ? ? = AE AD AC AB ? ? 二、等积模型 ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如下图 12 :: S S a b = ③夹在一组平行线之间的等积变形,如右图 ACD BCD S S= △△ ; 反之,如果 ACD BCD S S = △△ ,则可知直线AB平行于CD. ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. b a S2 S1 D C B A
三、蝶形定理 1、任意四边形中的比例关系(“蝶形定理”): ①1243::S S S S =或者1324S S S S ?=? ②()()1243::AO OC S S S S =++ 速记:上×下=左×右 蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面 可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 2、梯形中比例关系(“梯形蝶形定理”): ①2213::S S a b = ②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +. 四、相似模型 (一)金字塔模型 (二) 沙漏模型 G F E A B C D A B C D E F G ①AD AE DE AF AB AC BC AG ===; ②22:ADE ABC S S AF AG =△△:. 相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下: ⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; A B C D O b a S 3 S 2 S 1S 4 S 4 S 3 S 2 S 1O D C B A
六年级奥数专题几何五大模型鸟头模型
几何五大模型——鸟头模型 本讲要点 一两点都在边上:鸟头定理: (现出“鸟头模型”。然后按一下出现一个鸟头,勾勒出鸟头的轮廓,出现如图的鸟头几何模型。最后真实的鸟头隐去,只留下几何模型。最后按一下,出公式。) 二一点在边上,一点在边的延长线上:
例1 如图,AD=DB ,AE=EF=FC ,已知阴影部分面积为5平方厘米,△ ABC 的面积是平方厘米. 例2 例2 (1)如图在△ABC中,D、E分别是AB,AC上的点,且AD:AB=2:5, AE:AC=4:7,△ABC的面积是16平方厘米,求△ABC的面积。 (2)如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE 的面积是12平方厘米,求△ABC的面积。 例3 已知△DEF的面积为12平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC的面积。 例4 三角形ABC面积为1,AB边延长一倍到D,BC延长2倍到E,CA延长3倍到F,问三角形DEF的面积为多少 例5 长方形ABCD面积为120,EF为AD上的三等分点,G、H、I为DC上的四等分点,阴影面积是多大
如图,过平行四边形ABCD 内的一点P 作边AD 、BC 的平行线EF 、GH ,若PBD ?的面积为8平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米 1. 如下左图,在ABC △中,D 、E 分别是BC 、AB 的三等分点,且ABC △的面积是54,求CDE △的面积。 2. 如图,长方形ABCD 的面积是1,M 是AD 边的中点,N 在 AB 边上,且12AN BN =.那么,阴影部分的面积等于 . 3. 如图以ABC △的三边分别向外做三个正方形ABIH 、ACFG 、BCED ,连接HG 、EF 、ID , 又得到三个三角形,已知六边形DEFGHI 的面积是77平方厘米,三个正方形的面积分别是9、16、36平方厘米,则三角形ABC 的面积是多少 4. 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =; 延长CA 至F ,使3AF AC =,求三角形DEF 的面积。 5. 把四边形ABCD 的各边都延长2倍,得到一个新的四边形EFGH 。如果ABCD 的面积是5 平方厘米,则EFGH 的面积是多少 家庭作业 例6 A C E
小学奥数几何五大模型
几何五大模型 一、五大模型简介 (1)等积变换模型 1、等底等高的两个三角形面积相等; 2、两个三角形高相等,面积之比等于底之比,如图①所示, S[sub]1[/sub]:S[sub]2[/sub]=a:b; 3、两个三角形底相等,面积在之比等于高之比,如图②所示,S[sub]1[/sub]:S[sub]2[/sub]=a:b; 4、在一组平行线之间的等积变形,如图③所示, S[sub]△ACD[/sub]=S[sub]△BCD[/sub];反之,如果 S[sub]△ACD[/sub]=S[sub]△BCD[/sub], 则可知直线AB平行于CD。 例、如图,三角形ABC的面积是24,D、E、F分别是BC、AC、AD的中点,求三角形DEF的面积。
(2)鸟头(共角)定理模型 1、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形; 2、共角三角形的面积之比等于对应角(相等角或互补角)两夹边的乘积之比。 如图下图三角形ABC中,D、E分别是AB、AC上或AB、AC延长线上的点 则有:S[sub]△ABC[/sub]:S[sub]△ADE[/sub]=(AB×AC):(AD×AE) 我们现在以互补为例来简单证明一下共角定理!
如图连接BE,根据等积变化模型知,S[sub]△ADE[/sub]: S[sub]△ABE[/sub]=AD:AB、S[sub]△ABE[/sub]: S[sub]△CBE[/sub]=AE:CE,所以S[sub]△ABE[/sub]: S[sub]△ABC[/sub]=S[sub]△ABE[/sub]: (S[sub]△ABE[/sub]+S[sub]△CBE[/sub])=AE:AC ,因此S[sub]△ADE[/sub]:S[sub]△ABC[/su b]=(S[sub]△ADE[/sub]:S[sub]△ABE[/sub])×(S[sub]△ABE[/sub]:S[sub]△ABC[/sub])=(AD:AB)×(AE:AC)。 例、如图在ΔABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2, △ADE的面积为12平方厘米,求ΔABC的面积。
小学奥数-几何五大模型
模型四 相似三角形模型 (一)金字塔模型 (二) 沙漏模型 ①AD AE DE AF AB AC BC AG ===; ②22:ADE ABC S S AF AG =△△:。 所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下: ⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线。 三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半。 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具。 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形。 【例 1】 如图,已知在平行四边形ABCD 中,16AB =,10AD =,4BE =,那么FC 的长 度是多少? 【解析】 图中有一个沙漏,也有金字塔,但我们用沙漏就能解决问题,因为AB 平行于CD , 所以::4:161:4BF FC BE CD ===,所以4 10814 FC =?=+. 【例 2】 如图,测量小玻璃管口径的量具ABC ,AB 的长为15厘米,AC 被分为60等份。 如果小玻璃管口DE 正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径DE 是多大? 【解析】 有一个金字塔模型,所以::DE AB DC AC =,:1540:60DE =,所以10DE =厘米。 【例 3】 如图,DE 平行BC ,若:2:3AD DB =,那么:ADE ECB S S =△△________。 【解析】 根据金字塔模型:::2:(23)2:5AD AB AE AC DE BC ===+=, 22:2:54:25ADE ABC S S ==△△, 任意四边形、梯形与相似模型
小学奥数平面几何五大模型
小学奥数平面几何五大定律 一、等积模型 图(1) 图(2) 图(3) 图(4) ① 等底等高的两个三角形面积相等 如图(1):D 为BC 中点,则S△ABD=S△ACD 如图(4):l1平行于l2,则S△ACD=S△BCD ② 两个三角形高相等,面积比等于它们的底之比 如图(2): S △ABDS △ACD=BDCD ③ 两个三角形底相等,面积比等于它们的高之比 如图(3):BC=EF ,则 S △ABCS △DEF=h1h2 ④ 夹在一组平行线之间的等积变形 如图(4):l1平行于l2 ,则 S△ABD=S△ACD 反之如果S△ABD=S△ACD,则可知直线l1平行于l2 ⑤ 等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平 行四边形) ⑥ 三角形面积等于与它等底等高的平行四边形面积的一半 ⑦ 两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底 相等,面积比等于它们的高之比 二、共角定理(鸟头定理) 两个三角形中有一个角相等或互补(两个角之和=180O ),这两个三角形叫做共角三角形. D B h A B D C h1 h2 l2 l2 B C h1 F E D h2 B C D h
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 共角 互补角 图(1) 图(2) 如图(1):在△ABC 中,D 、E 分别是AB 、AC 上的点,△ABC 与△ADE 共∠A 如图(2):D 在BA 的延长线上,E 在AC 上;∠BAC+∠BAC =180O (互补), 则: S △ABC :S △ADE =(AB ×AC):(AD ×AE);或 S △ABCS △ADE=AB × ACAD × AE 三、相似模型 数学上,相似指两个图形的形状完全相同,其中一个图形能通过放大、缩小、平移、旋转、镜像等方式变成另一个。 相似比:是指两个相似图形的对应边的比值。 相似符号:“∽” 相似三角形:三角分别相等,三边成比例的两个三角形叫做相似三角形 相似三角形传递性:如果图A 相似于图B ,图B 相似于C ,则 A 相似C 即:图A ∽图B ,图B ∽图C ;则,图A ∽图B ∽图C a 顺时针旋转90度 a 翻转 a 缩小 图(1) 图(2) 图(3) 图(4) c a d b A B C D E A D E F C B D E O B A
小学奥数-几何五大模型
模型三 蝴蝶模型(任意四边形模型) 任意四边形中的比例关系(“蝴蝶定理”): ①1243::S S S S =或者1324S S S S ?=? ②()()1243::AO OC S S S S =++ 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。 【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△ AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米 【分析】 根据蝴蝶定理求得312 1.5AOD S =?÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平 方千米,所以人工湖的面积是7.5 6.920.58-=平方千米 【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知, 求:⑴三角形BGC 的面积;⑵:AG GC = 【解析】 ⑴根据蝴蝶定理,123BGC S ?=?V ,那么6BGC S =V ; ⑵根据蝴蝶定理,()():12:361:3AG GC =++=. () 【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。如果三角形ABD 的面积等于三角形BCD 的 面积的1 3 ,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。 【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已 知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。看到题目中给出条件:1:3ABD BCD S S =V V ,这可以向模型一蝴蝶定理靠拢,于是得出一种解法。又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形”,于是可以作AH 垂直BD 于H ,CG 垂直BD 于G ,面积比转化为高之比。再应用结论:三角形高相同,则面积之比等于底边之比,得出结果。请老师注意比较两种解法,使学生体会到蝴蝶定理的优势,从而主观上愿意掌握并使用蝴蝶定理解决问题。 解法一:∵::1:3ABD BDC AO OC S S ??==, ∴236OC =?=, ∴:6:32:1OC OD ==. 解法二:作AH BD ⊥于H ,CG BD ⊥于G . ∵1 3 ABD BCD S S ??=, 任意四边形、梯形与相似模型
小学奥数几何五大模型(蝴蝶模型)
模型三蝴蝶模型(任意四边形模型) 任意四边形中的比例关系 (“蝴蝶定理”):S 4S 3 S 2S 1O D C B A ①12 43::S S S S 或者1324S S S S ②124 3::AO OC S S S S 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。 【例1】(小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△ AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是 6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米? O D C B A 根据蝴蝶定理求得312 1.5AOD S △平方千米,公园四边形ABCD 的面积是123 1.57.5平方千米,所以人工湖的面积是7.5 6.920.58平方千米 【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知, 求:⑴三角形BGC 的面积;⑵ :AG GC ?A B C D G 321 ⑴根据蝴蝶定理,123BGC S ,那么6BGC S ;⑵根据蝴蝶定理,:12:361:3AG GC .(???)任意四边形、梯形与相似模型
【例2】四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。如果三角形ABD 的面积等于三角形 BCD 的面积的1 3,且2AO ,3DO ,那么CO 的长度是DO 的长度的_________倍。A B C D O H G A B C D O 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形” ,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。看到题目中给出条件 :1:3ABD BCD S S ,这可以向模型一蝴蝶定理靠拢,于是得出一种解法。又观察题目中给出的已知 条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造 这个”不良四边形”,于是可以作AH 垂直BD 于H ,CG 垂直BD 于G ,面积比转化为高之比。再应用结论:三角形高相同,则面积之比等于底边之比,得出结果。请老师注意比较两种解法,使学 生体会到蝴蝶定理的优势,从而主观上愿意掌握并使用蝴蝶定理解决问题。 解法一:∵::1:3ABD BDC AO OC S S ,∴236OC , ∴:6:32:1OC OD . 解法二:作AH BD 于H ,CG BD 于G .∵1 3 ABD BCD S S ,∴1 3AH CG ,∴13AOD DOC S S ,∴13AO CO ,∴236OC , ∴:6:32:1OC OD . 【例3】如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是 2、4、4和6。求:⑴求OCF △的面积;⑵求GCE △的面积。 O G F E D C B A ⑴根据题意可知,BCD △的面积为244616,那么BCO △和CDO 的面积都是162 8,所以OCF △的面积为844;⑵由于BCO △的面积为8,BOE △的面积为6,所以OCE △的面积为862, 根据蝴蝶定理, ::2:41:2COE COF EG FG S S ,所以::1:2GCE GCF S S EG FG ,那么1 1 2 21233 GCE CEF S S .【例4】图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的
奥数专题:几何五大模型(鸟头模型)
鸟头模型 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2), 则:():()ABC ADE S S AB AC AD AE =??△△ E D C B A E D C B A 图⑴ 图⑵ 【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16 ADE S =△平方厘米,求ABC △的面积. E D C B A E D C B A 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===??△△, ::4:7(45):(75)ABE ABC S S AE AC ===??△△,所以:(24):(75)ADE ABC S S =??△△,设8ADE S =△份, 则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等
于1,那么三角形ABC 的面积是多少? E D C B A A B C D E 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S =V V 又∵5AB AD = ∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V . 【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =, 乙部分面积是甲部分面积的几倍? 乙 甲 E D C B A A B C D E 甲 乙 【解析】 连接AD . ∵3BE =,6AE = ∴3AB BE =,3ABD BDE S S =V V 又∵4BD DC ==, ∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲. 【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =, :3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积. E D C B A E D C B A 【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===??△△ []::3:(32)(35):(32)5ABE ABC S S AE AC ==+=?+?△△,
小学奥数-几何五大模型(等高模型)知识分享
小学奥数-几何五大模型(等高模型)
模型一 三角形等高模型 已经知道三角形面积的计算公式: 三角形面积=底?高2÷ 从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小); 这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13 ,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如图 12::S S a b = b a S 2S 1 D C B A ③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD . ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比; 三角形等高模型与鸟头模型
两个平行四边形底相等,面积比等于它们的高之比.
【例 1】 你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三角形;⑵ 4个面积相等 的三角形;⑶6个面积相等的三角形。 【解析】 ⑴ 如下图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点,答案不唯一: C E D B A F C D B A G D B A ⑵ 如下图,答案不唯一,以下仅供参考: ⑸ ⑷⑶⑵⑴ ⑶如下图,答案不唯一,以下仅供参考: 【例 2】 如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上。 ⑴ 求三角形ABC 的面积是三角形ABD 面积的多少倍? ⑵ 求三角形ABD 的面积是三角形ADC 面积的多少倍? 【解析】 因为三角形ABD 、三角形ABC 和三角形ADC 在分别以BD 、 BC 和DC 为底时,它们的高都是从A 点向BC 边上所作的垂 线,也就是说三个三角形的高相等。 于是:三角形ABD 的面积12=?高26÷=?高 三角形ABC 的面积124=+?()高28÷=?高 三角形ADC 的面积4=?高22÷=?高 所以,三角形ABC 的面积是三角形ABD 面积的4 3 倍; 三角形ABD 的面积是三角形ADC 面积的3倍。 【例 3】 如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影 部分的面积是 平方厘米。 【解析】 图中阴影部分的面积等于长方形ABCD 面积的一半,即4326?÷=(平方厘米)。 C D B A
小学奥数-几何五大模型(等高模型)
模型一三角形等高模型 已经知道三角形面积的计算公式: 三角形面积底高2 从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小); 这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化?但是,当三角形的底和高同时 1 发生变化时,三角形的面积不一定变化?比如当高变为原来的3倍,底变为原来的1,则三角形面积与原来 3 的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化. 同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如图S i :S2 a:b ③夹在一组平行线之间的等积变形,如右上图S A ACD S A BCD ; 反之,如果S A ACD S A BCD,则可知直线AB平行于CD ? ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比; 两个平行四边形底相等,面积比等于它们的高之比.
你有多少种方法将任意一个三角形分成: ⑴3个面积相等的三角形; ⑵4个面积相等的三角形; ⑶ 6个面积相等的三角形。 ⑴ 如下图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点,答案不唯一: ⑵ 如下图,答案不唯一,以下仅供参考: 如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上。 ⑴ 求三角形ABC 的面积是三角形 ABD 面积的多少倍? ⑵求三角形ABD 的面积是三角形 ADC 面积的多少倍? 因为三角形 ABD 、三角形 ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时,它们的高都是从 A 点向BC 边上所作的垂线,也就是说三个三角形的高相等。 于是:三角形ABD 的面积 12高2 6高 三角形ABC 的面积 (12 4)高2 8高 三角形ADC 的面积 4高2 2高 4 所以,三角形 ABC 的面积是三角形 ABD 面积的-倍; 3 三角形ABD 的面积是三角形 ADC 面积的3倍。 如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影部分的面 积是 平方厘米。 D C 图中阴影部分的面积等于长方形 ABCD 面积的一半,即4 3 2 6(平方厘米)。 (2009年四中小升初入学测试题)如图所示,平行四边形的面积是 50平方厘米,则阴影部分的面积 是 平方厘米。 【例1】 【解 【例2】 【解析】 【例3】 【解析】 ⑶如下图,答案不唯一,以下仅供参考:
小学的奥数几何五大模型燕尾模型
燕尾定理: 在三角形ABC 中,AD ,BE ,CF 相交于同一点O , 那么, 上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ?和ACO ?的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积. 通过一道例题 证明燕尾定理: 如右图,D 是BC 1423:::S S S S BD DC == 【解析】 三角形BED 与三角形CED 同高,分别以BD 、DC 为底,所以有14::S S BD DC =; 三角形ABE 与三角形EBD 同高,12::S S ED EA =; 三角形ACE 与三角形CED 同高,43::S S ED EA =,所以1423::S S S S =; 综上可得, 1423:::S S S S BD DC ==. 【例 1】 (2009年第七届希望杯五年级一试试题)如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 . 【解析】 方法一:连接CF , 根据燕尾定理, 12ABF ACF S BD S DC ==△△,1ABF CBF S AE S EC ==△△, 设1BDF S =△份,则2DCF S =△份,3ABF S =△份,3AEF EFC S S ==△△份,如图所标 所以55 12 12 DCEF ABC S S ==△ 方法二:连接DE ,由题目条件可得到1133 ABD ABC S S ==△△, 1121 2233 ADE ADC ABC S S S ==?=△△△,所以 11 ABD ADE S BF FE S ==△△, 1111111 22323212 DEF DEB BEC ABC S S S S =?=??=???=△△△△, 而211323CDE ABC S S =??=△△.所以则四边形DFEC 的面积等于512 . 【巩固】如图,已知BD DC =,2EC AE =,三角形ABC 的面积是30,求阴影部分面积. 【解析】 题中条件只有三角形面积给出具体数值,其他条件给出的实际上是比例的关系, 由此我们可以初步判断这道题不应该通过面积公式求面积. 又因为阴影部分是 一个不规则四边形,所以我们需要对它进行改造,那么我们需要连一条辅助线, (法一)连接CF ,因为BD DC =,2EC AE =,三角形ABC 的面积是30, 所以1103 ABE ABC S S ==△△,1152 ABD ABC S S ==△△. 例题精讲 燕尾定理
- 小学奥数-几何五大模型(等高模型)
- 小学奥数-几何五大模型(鸟头模型).
- 小学奥数-几何五大模型
- 小学奥数-几何五大模型(相似模型)
- 小学奥数_几何五大模型(鸟头模型)
- 六年级奥数专题几何五大模型鸟头模型
- 小学奥数之几何五大模型
- 小学奥数几何五大模型
- 小学奥数 几何五大模型 等高模型
- 小学奥数-几何五大模型(等高模型)讲课教案
- 小学奥数-几何五大模型(蝴蝶模型)
- (完整版)小学奥数-几何五大模型(相似模型)
- 小学奥数之几何五大模型精编版
- 小学平面几何五大模型
- 几何五大模型汇总
- 小高奥数几何-三角形五大模型及例题解析
- 小学奥数之几何五大模型
- 小学奥数-几何五大模型.doc
- 小学奥数几何五大模型(蝴蝶模型)
- 小学奥数-几何五大模型(鸟头模型)
