VGA3+6接法

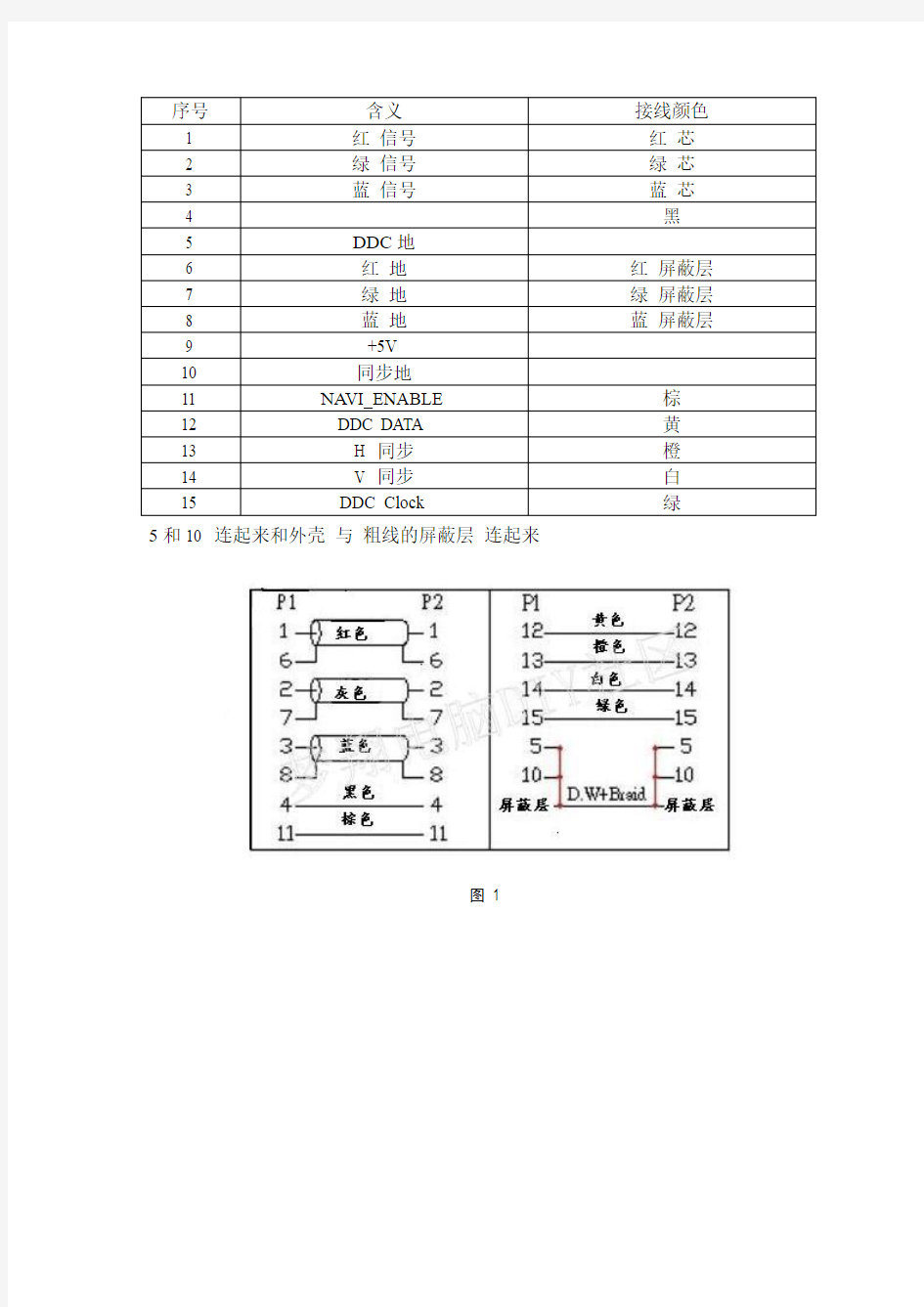
5和10 连起来和外壳与粗线的屏蔽层连起来

图 1

图 2

黄金分割法,进退法,原理及流程图

1黄金分割法的优化问题 （1）黄金分割法基本思路： 黄金分割法适用于[a，b]区间上的任何单股函数求极小值问题，对函数除要求“单谷”外不做其他要求，甚至可以不连续。因此，这种方法的适应面非常广。黄金分割法也是建立在区间消去法原理基础上的试探方法，即在搜索区间[a，b]内适当插入两点a1，a2，并计算其函数值。a1，a2将区间分成三段，应用函数的单谷性质，通过函数值大小的比较，删去其中一段，是搜索区间得以缩小。然后再在保留下来的区间上作同样的处理，如此迭代下去，是搜索区间无限缩小，从而得到极小点的数值近似解。 （2）黄金分割法的基本原理 一维搜索是解函数极小值的方法之一，其解法思想为沿某一已知方向求目标函数的极小值点。一维搜索的解法很多，这里主要采用黄金分割法（0.618法）。该方法用不变的区间缩短率0.618代替斐波那契法每次不同的缩短率，从而可以看成是斐波那契法的近似，实现起来比较容易，也易于人们所接受。

黄金分割法是用于一元函数f(x)在给定初始区间[a,b]内搜索极小点α*的一种方法。它是优化计算中的经典算法，以算法简单、收敛速度均匀、效果较好而著称，是许多优化算法的基础，但它只适用于一维区间上的凸函数[6]，即只在单峰区间内才能进行一维寻优，其收敛效率较低。其基本原理是：依照“去劣存优”原则、对称原则、以及等比收缩原则来逐步缩小搜索区间[7]。具体步骤是：在区间[a,b]内取点：a1 ，a2 把[a,b]分为三段。如果f(a1)>f(a2)，令 a=a1,a1=a2,a2=a+r*(b-a)；如果f(a1)

[设计]罚函数法MATLAB程序

[设计]罚函数法MATLAB程序 一、进退法、0.618法、Powell法、罚函数法的Matlab程序设计罚函数法(通用) function y=ff(x,k) y=-17.86*0.42*x(1)/(0.8+0.42*x(1))*(1-exp(- 2*(0.8+0.42*x(1))/3))*exp(-1.6)*x(2)-22. 99*x(1)/(0.8+x(1))*(1-exp(-2*(0.8+x(1))/3))*x(3)+k*(x(2)- (1.22*10^2*(9517.8*exp(-1 .6-2*0.42*x(1)/3)*x(2)+19035.6*exp(- 2*x(1)/3)*x(3)))/(1.22*10^2+9517.8*exp(-1.6-2 *0.42*x(1)/3)*x(2)+19035.6*exp(-2*x(1)/3)*x(3)))^2+k*(x(3)-exp(-0.8-2*x(1)/3)*x(3) -exp(-2.4-2*0.42*x(1)/3)*x(2))^2; % 主函数，参数包括未知数的个数n，惩罚因子q，惩罚因子增长系数k，初值x0，以及允许的误差r function G=FHS(x0,q,k,n,r,h,a) l=1; while (l) x=powell(x0,n,q,r(1),h,a); %调用powell函数 g(1)=ff1(x),g(2)=ff2(x) . . . g(p)=ffp(x); %调用不等式约束函数，将其值 %存入数组g h(1)=hh1(x),h(2)=hh2(x) . . . h(t)=hht(x); %调用等式约束函数，将其值%存入数组h for i=1:p

机械优化设计试验指导书114830复习过程

机械优化设计实验指导书 实验一用外推法求解一维优化问题的搜索区间 一、实验目的： 1、加深对外推法（进退法）的基本理论和算法步骤的理解。 2、培养学生独立编制、调试机械优化算法程序的能力。 3、培养学生灵活运用优化设计方法解决工程实际问题的能力。 二、主要设备及软件配置 硬件：计算机（1台/人） 软件：VC6.0（Turbo C） 三、算法程序框图及算法步骤

外推法（进退法）程序框图1-1 图 算法程序框图：如图1-1所示。 算法步骤：（1）选定初始点a1=0, 初始步长h＝h0，计算 y1＝f(a1)， a2=a1＋h,y2＝f(a2)。 （2）比较y1和y2: （a）如y1≤y2, 向右前进；，转（3）； （b）如y2＞y1, 向左后退；h＝－h，将a1与a2，y1与y2的 值互换。转（3）向后探测； (3）产生新的探测点a3＝a2＋h，y3＝f(a3); (4) 比较函数值 y2和y3： （a）如y2>y3, 加大步长 h＝2h ，a1=a2, a2=a3,转（3）继续探测。 （b）如y2≤y3,则初始区间得到：a=min[a1,a3]， b=max[a3,a1]， 函数最小值所在的区间为[a， b] 。 四、实验内容与结果分析 1、根据算法程序框图和算法步骤编写计算机程序; 2-8x+9的搜索区间，初始点a1=0,、求解函数f(x)=3x初始步长h0=0.1; 23、如果初始点a1=1.8,初始步长h0=0.1,结果又如何？ 4、试分析初始点和初始步长的选择对搜索计算的影响。

实验二用黄金分割法求解一维搜索问题 一、实验目的： 1、加深对黄金分割法的基本理论和算法步骤的理解。 2、培养学生独立编制、调试机械优化算法程序的能力。 3、培养学生灵活运用优化设计方法解决工程实际问题的能力。 二、主要设备及软件配置 硬件：计算机（1台/人） 软件：VC6.0（Turbo C） 三、算法程序框图及算法步骤 黄金分割法程序框图图1-2 1-2所示。算法程序框图：如图算法步骤：。0.618及收敛精度ε，将λ赋以b]，[a）给出初始搜索区间1． 2）按坐标点计算公式计算a1,a2；并计算其对应的函数值y1,y2。 3）根据区间消去法原理缩短搜索区间。为了能用原来的坐标点计算公式，需进行区间名称的代换，并在保留区间中计算一个新的试验点及其函数值。 如果y1≥y2，则新区间＝[a1 b]，a=a1,a1=a2,y1=y2,

黄金分割法,进退法,原理及流程图

1黄金分割法的优化问题（1）黄金分割法基本思路： 黄金分割法适用于[a，b]区间上的任何单股函数求极小值问题，对函数除要求“单谷”外不做其他要求，甚至可以不连续。因此，这种方法的适应面非常广。黄金分割法也是建立在区间消去法原理基础上的试探方法，即在搜索区间[a，b]内适当插入两点a1，a2，并计算其函数值。a1，a2将区间分成三段，应用函数的单谷性质，通过函数值大小的比较，删去其中一段，是搜索区间得以缩小。然后再在保留下来的区间上作同样的处理，如此迭代下去，是搜索区间无限缩小，从而得到极小点的数值近似解。 （2）黄金分割法的基本原理 一维搜索是解函数极小值的方法之一，其解法思想为沿某一已知方向求目标函数的极小值点。一维搜索的解法很多，这里主要采用黄金分割法（法）。该方法用不变的区间缩短率代替斐波那契法每次不同的缩短率，从而可以看成是斐波那契法的近似，实现起来比较容易，也易于人们所接受。 黄金分割法是用于一元函数f(x)在给定初始区间[a,b]内搜索极小点α*的一种方法。它是优化计算中的经典算法，以算法简单、收敛速度均匀、效果较好而着称，是许多优化算法的基础，但它只适用于一维区间上的凸函数[6]，即只在单峰区间内才能进行一维寻优，其收敛效率较低。其基本原理是：依照“去劣存优”原则、对称原则、以及等比收缩原则来逐步缩小搜索区间[7]。具体步骤是：在区间[a,b]内取点：a1 ，a2 把[a,b]分为三段。如果

f(a1)>f(a2)，令a=a1,a1=a2,a2=a+r*(b-a)；如果f(a1)

黄金分割法-进退法-原理及流程图

黄金分割法-进退法-原理及流程图

1黄金分割法的优化问题 （1）黄金分割法基本思路： 黄金分割法适用于[a，b]区间上的任何单股函数求极小值问题，对函数除要求“单谷”外不做其他要求，甚至可以不连续。因此，这种方法的适应面非常广。黄金分割法也是建立在区间消去法原理基础上的试探方法，即在搜索区间[a，b]内适当插入两点a1，a2，并计算其函数值。a1，a2将区间分成三段，应用函数的单谷性质，通过函数值大小的比较，删去其中一段，是搜索区间得以缩小。然后再在保留下来的区间上作同样的处理，如此迭代下去，是搜索区间无限缩小，从而得到极小点的数值近似解。 （2）黄金分割法的基本原理 一维搜索是解函数极小值的方法之一，其解法思想为沿某一已知方向求目标函数的极小值点。一维搜索的解法很多，这里主要采用黄金分割法（0.618法）。该方法用不变的区间缩短率0.618代替斐波那契法每次不同的缩短率，从而可以看成是斐波那契法的近似，实现起来比较容易，也易于人们所接受。

黄金分割法是用于一元函数f(x)在给定初始区间[a,b]内搜索极小点α*的一种方法。它是优化计算中的经典算法，以算法简单、收敛速度均匀、效果较好而著称，是许多优化算法的基础，但它只适用于一维区间上的凸函数[6]，即只在单峰区间内才能进行一维寻优，其收敛效率较低。其基本原理是：依照“去劣存优”原则、对称原则、以及等比收缩原则来逐步缩小搜索区间[7]。具体步骤是：在区间[a,b]内取点：a1 ，a2 把[a,b]分为三段。如果f(a1)>f(a2)，令 a=a1,a1=a2,a2=a+r*(b-a)；如果f(a1)

matlab进退法,切线法求极值

7、用进退法求极值： ()21036 f x x x =--；a=0.5，h=0.5,ε =0.01。 %建立函数f（x）。 function y=f(x) if nargin==1 y=x^2-10*x-36; end end %建立用进退法求解极值的程序。function y=jintui(a,h,e) a=input('enter the value of a:'); h=input('enter the value of h:'); e=input('enter the value of e:'); m=1;n=1; x0=a; x1=x0+h; while abs(x1-x0)>e if f(x0)>f(x1) x0=x1; x1=x0+h*2^m; m=m+1;

else x1=x0; x0=x1-h/2^n; n=n+1; end end x=(x0+x1)/2; y=f(x); end 运行结果如下： enter the value of a:0.5 enter the value of h:0.5 enter the value of e:0.01 ans = -59.9922 8、用切线法求极值： ()21635 f x x x =-+； %建立原函数；function y=f(x) if nargin==1 y=x^2-16*x+35;

end end %建立一阶导函数； function yd=fd(x) if nargin==1 yd=2*x-16; end end %建立二阶导函数； function ydd=fdd(x) if nargin==1 ydd=2; end end %切线法求极值函数； %x0为给定的初值，n为计算次数； %f（x）、fd（x）、fdd（x）分别为原函数，一阶导函数，二阶导函数；function [xj,yj]=qiexian(x0,n) x0=input('Please enter the value of x0:'); n=input('Please enter the value of n:'); for k=1:1:n x1=x0-fd(x0)/fdd(x0);

多维搜索算法程序

拟牛顿算法 一、算法流程图/算法步骤 1、DFP算法： （1）算法步骤： 2、BFGS算法 （1）算法步骤： 3、模式搜索算法 （1）算法步骤：

二、程序代码 1、DFP算法 %拟牛顿法中DFP算法求解f=x1*x1+2*x2*x2-2*x1*x2-4*x1的最小值tic format long syms x1 x2 r; f= x1*x1+2*x2*x2-2*x1*x2-4*x1; %要最小化的函数 x=[x1,x2]; df=jacobian(f,x); %函数f的偏导 df=df.'; x0=[0,0]'; g1=subs(df,x,x0); %起始点的梯度 epsilon=1e-6; %0.000001为搜索精度 k=0; H0=[1 0;0 1]; %初始矩阵为二阶单位阵 while(norm(g1)>epsilon) %迭代终止条件||g1||<=epsilon if k==0 d=-H0*g1; %负梯度方向 else H1=H0+pk*pk'/(qk'*pk)-H0*qk*qk'*H0/(qk'*H0*qk); d=-H1*g1;H0=H1; end z=subs(f,x,x0+r*d); %关于r的函数 result1=jintuifa(z,r); %进退法求下单峰区间 result2= gold(z,r,result1); %黄金分割法求最优步长 step=result2; x0=x0+step*d; g0=g1; g1=subs(df,x,x0);

%gk=double(gk); qk=g1-g0; pk=step*d; k=k+1; end k%最优点 x0 min=subs(f,[x1 x2],x0)%最优值 toc %进退法求下单峰区间 function result= jintuifa(y,r) t0=0;step=0.0125; t1=t0+step; ft0=subs(y,{r},{t0}); %step1 求f(t0) 将函数y中变量x替换为t0 ft1=subs(y,{r},{t1}); if (ft1<=ft0) %step3 step4 step=2*step; t2=t1+step; ft2=subs(y,{r},{t2}); while(ft1>ft2) t1=t2; step=2*step; t2=t1+step; ft1=subs(y,{r},{t1}); ft2=subs(y,{r},{t2}); end else %step5 step6 step=step/2; t2=t1; t1=t2-step; ft1=subs(y,{r},{t1}); while(ft1>ft0) step=step/2; t2=t1; t1=t2-step; ft1=subs(y,{r},{t1}); end end result=[t2]； %黄金分割法求最优步长 function result=gold(y,r,m) a=0;b=m;e=1e-5; a1=a+0.382*(b-a); %step1

优化设计作业及程序

优化设计程序及作业 1进退法求搜索区间程序： (x1) %定义函数为1为初始值，h为步长 (x)x^2-7*10; f1(x1)21; f2(x2); f1j f1(x1); f2(x2); f1

x1(1)*(); 1; x12; x2*(); ('所求最优解') ()/2 ('所求函数') (x) 在命令窗口运行（3.4，3.6，0.01）得到 所求最优解： x =3.4798 所求函数值： y = -2.2496 黄金分割总程序 (q1) %定义黄金分割法为，x1为初始值，h为初始步长，j为初始精度(x)x^2-7*10; f1(q1)21; f2(q2); f1

3; 0.6180339887; c1(1)*(); c2*(); ()>j f1(c1); f2(q2); f1j 1:2 1

黄金分割法进退法求极小值matlab程序

%%%%%%%%%%%%%%%%%%%%%%%%%%-----进退法求合适区间-------%%%%%%%%%%%%%%%%%%%%%%%%%%%%% clear; syms x; %创建一个符号变量 h=diff(f(x),x); %求对x的一阶导数 x0=10; g=subs(h,x0); %在x0处h的值 %%%%%%%%---------初始值在极小值点左侧的时候-------%%%%%%%%%%%%%%%%%%%%%%%%%%%%% if g<0 step=10;x1=x0+step; if f(x1)<=f(x0) step=2*step; x2=x1+step; while f(x1)>f(x2) x0=x1;x1=x2; step=2*step; x2=x1+step; end else step=0.5*step; x2=x1-step; while f(x0)>f(x2) x0=x0+0.5*step; x2=x2+step; end end a=x0; b=x2; disp(['f(x)极小值点所在区间为（',num2str(a),',',num2str(b),')']); end %%%%%%%%%%%%%%%%%%%%当极小值点在初始点右侧时%%%%%%%%%%% if g>0 step=6;x1=x0-step;%以下方法仅仅适用于初始值在极小值点右侧的时候 if f(x1)<=f(x0) step=2*step; x2=x1-step; while f(x1)>f(x2) x0=x1;x1=x2; step=2*step; x2=x1-step; end

罚函数法MATLAB程序

一、进退法、0.618法、Powell法、罚函数法的Matlab程序设计 罚函数法（通用） function y=ff(x,k) y=-17.86*0.42*x(1)/(0.8+0.42*x(1))*(1-exp(-2*(0.8+0.42*x(1))/3))*exp(-1.6)*x(2)-22. 99*x(1)/(0.8+x(1))*(1-exp(-2*(0.8+x(1))/3))*x(3)+k*(x(2)-(1.22*10^2*(9517.8*exp(-1 .6-2*0.42*x(1)/3)*x(2)+19035.6*exp(-2*x(1)/3)*x(3)))/(1.22*10^2+9517.8*exp(-1.6-2 *0.42*x(1)/3)*x(2)+19035.6*exp(-2*x(1)/3)*x(3)))^2+k*(x(3)-exp(-0.8-2*x(1)/3)*x(3) -exp(-2.4-2*0.42*x(1)/3)*x(2))^2; % 主函数，参数包括未知数的个数n，惩罚因子q，惩罚因子增长系数k，初值x0，以及允许的误差r function G=FHS(x0,q,k,n,r,h,a) l=1; while (l) x=powell(x0,n,q,r(1),h,a); %调用powell函数 g(1)=ff1(x),g(2)=ff2(x) . . . g(p)=ffp(x); %调用不等式约束函数，将其值%存入数组g h(1)=hh1(x),h(2)=hh2(x) . . . h(t)=hht(x); %调用等式约束函数，将其值 %存入数组h for i=1:p if g(i)

机械优化设计c语言程序

计算f(x1,x2)=x0^2+x1^2-x0*x1-10*x0-4*x1+60 #include "stdio.h" #include "stdlib.h" #include "math.h" double objf(double x[]) {double ff; ff=x[0]*x[0]+x[1]*x[1]-x[0]*x[1]-10*x[0]-4*x[1]+60; return(ff); } void jtf(double x0[],double h0,double s[],int n,double a[],double b[]) {int i; double *x[3],h,f1,f2,f3; for(i=0;i<3;i++) x[i]=(double *)malloc(n*sizeof(double)); h=h0; for(i=0;i

*(x[1]+i)=*(x[0]+i)+h*s[i]; f2=objf(x[1]); if(f2>=f1) {h=-h0; for(i=0;i

优化设计Matlab程序

进退法步骤： 1. 给定初始点(0)x ，初始步长0h ，令(1)(0)0,,0h h x x k === 2. 令(4)(1),1x x h k k =+=+ 3. 若(4)(1)()()f x f x <，则转4，否则转5 4. (2)(1)(1)(4)(2)(1)(1)(4),,()(),()()x x x x f x f x f x f x ====，令h =2h ，转2 5. 若k =1，则转6，否则转,7 6. 令h =-h ，(2)(4)(2)(4),()()x x f x f x ==，转2 7. 令(3)(2)(2)(1)(1)(4),,x x x x x x ===，停止计算，极小点包含于区间(1)(3)[,]x x 或 (3)(1)[,]x x %目标函数：f %初始点：x0 %初始步长：h0 %精度：eps %目标函数取包含极值的区间左端点：minx %目标函数取包含极值的区间右端点：maxx function [minx,maxx] = minJT(f,x0,h0,eps) format long ; if nargin == 3 eps = 1.0e-6; end x1 = x0; k = 0; h = h0; while 1 x4 = x1 + h; k = k+1; f4 = subs(f, findsym(f),x4); ! subs : Symbolic substitution in symbolic expression or matrix f1 = subs(f, findsym(f),x1); ! findsym : Determine variables in symbolic expression or matrix if f4 < f1 x2 = x1; x1 = x4; f2 = f1; f1 = f4; h = 2*h; else if k==1 h = -h; x2 = x4;

掌握进退法和区间消去法原理

掌握进退法和区间消去法原理 当采用数学规划法寻求多元函数的极值点时，一般要进行一系列如下格式的迭代计算: 当方向 给定，求最佳步长 就是求一元函数 : 的极值问题，这一过程被称为一维搜索. 确定最优解所在区间的进退法： 一、 一维搜索的基本思想 1、单谷(峰）区间 在给定区间内仅有一个 谷值的函数称为单谷数，其 区间称为单谷区间。 函数值：“大－小－大” 图形：“高—低—高” 2. 找初始单谷区间是一维 搜索的第一步； 第二步使区间缩小。 二、确定初始单谷区间的进退法： 基本思想： 对f (x )任选一个初始点a 1及初始步长h ， 通过比较这两点函数值的大小，确定第三点位置，比较这三点的函数值大小， 1 (0,1,2, ) k k k k s k α+=+=x x 1 ()()() k k k k k f f s α?α+=+=x x

确定是否为“高—低—高” 形态。 步骤： （1）选定初始点a1, 初始步长h＝h0 > 0，计算 y1＝f(a1)， y2＝f(a1＋h)。 （2）比较y1和y2。 （a）如y1>y2, 向右前进；加大步长 h＝2 h ，转（3）向前； （b）如y1y3, 加大步长 h＝2 h(也可不变) ，a1=a2, a2=a3, 转（3）继续探测。 （a）如y2

进退法程序改好的

进退法 进退法基本思想： 对f(x)任选一个初始点x1及初始步长h0，通过比较这两点函数值的大小，确定第三点位置，比较这三点的函数值大小，确定是否为“高—低—高”形态。 （1）选定初始点x0, 初始步长h＝h0，计算 y1＝f(x1)，y2＝f(x1＋h)。 （2）比较y1和y2。 （a）如y1≤y2, 向左后退；h＝－h0，将x1与x2，y1与y2的值互换，转（3）向后探测； （b）如y1＞y2, 向右前进；加大步长 h＝2 h，转（3）向前探测；（3）产生新的探测点x3＝x1＋h，y3＝f( x3); （4) 比较函数值 y2与y3。 （a）如f2＞f3, 加大步长 h＝2 h ，x1=x2, x2=x3,转（3）继续搜索。 （b）如f2≤f3, 则初始区间得到：a=min[x1,x3]， b=max[x3,x1]，函数最小值所在的区间为[a, b]。 #include"stdio.h" #include #define f(x) x*x-7*x+10 void main() { float y1,y2,y3,x0,x1,x2,x3,h,h0,a,b; scanf("%f%f",&x0,&h0); h=h0,x1=x0;y1=f(x1);x2=x1+h;y2=f(x2); if(y1<=y2) {

h=-1*h0;x3=x1;y3=y1;x1=x2;y1=y2;x2=x3;y2=y3;h=2*h;x3=x2+h; y3=f(x3); } else { h=2*h;x3=x2+h;y3=f(x3); } while(y2>y3) { x1=x2; y1=y2; x2=x3; y2=y3; h=2*h; x3=x2+h; y3=f(x3); } if(h<0) { a=x3;b=x1; printf("a=%f,b=%f",a,b); } else { a=x1;b=x3; printf("a=%f,b=%f",a,b); } }

最优化数值实验三

最优化数值实验报告三 实验目的： 1， 能够对具体的问题用合适的最优化方法进行求解。 2， 对同一个问题用不同的优化方法进行求解并比较其优劣。 实验内容：（主要是《最优化练习题017》中的3，4，5题） (1)设某实验对象的变化规律可由专业知识得出下列函数 c ae x y x b +=/)( a,b,c 的具体数值，将实验对象的变化规律写出。进一步，如果根据专业知识，知道待定参 数a,b,c 还满足下列条件：15tan 22 =++c b a ,那么结果又是如何？请你写出求解的数学思想，求解的全过程，并分析你的方法的优缺点。 解： 首先将问题表示为最小二乘问题的模型，即是将目标函数写成若干个函数的平方和的形式，一般可以写成 ∑==m i i x f x f 1 2)()( 其中T n x x x x ),...,,(21=是n R 中的点。一般假设n m ≥，最小而成问题就是求 ∑==m i i x f x f 1 2) ()(min 对于本题而言，有m=8,且 60 .15)(,30.15)(,73.14)(,15.14)(,93.12)(,63.11)(,88.8)(,05.5)(0.16/80.11/77/60.5/50.3/40.2/30.1/220.0/1-+=-+=-+=-+=-+=-+=-+=-+=c ae x f c ae x f c ae x f c ae x f c ae x f c ae x f c ae x f c ae x f b b b b b b b b 所以问题转化为求 ∑==8 1 2) ()(min i i x f x f 通过在前次实验中对各种无约束问题的算法分析和比较知道，BFGS 是当中一种性能比较好的，所以首先我们采用BFGS 法。（同前两次实验，jintuifa 和gold 对应进退法和黄金分割法。见附录） 程序：

黄金分割法、二次插值法C语言编程

已知：F(x)=x4-4x3-6x2-16x+4,求极小值，极小值点，区间，迭代次数？用进退法确定区间，用黄金分割法求极值。 #include #include #define e 0.001 #define tt 0.01 float f(double x) { float y=pow(x,4)-4*pow(x,3)-6*pow(x,2)-16*x+4; return(y); } finding(float *p1,float*p2) { float x1=0,x2,x3,t,f1,f2,f3,h=tt; int n=0; x2=x1+h;f1=f(x1);f2=f(x2); if(f2>f1) {h=-h;t=x2;x2=x1;x1=t;} do { x3=x2+h;h=2*h;f3=f(x3);n=n+1;} while(f3x3) {t=x1;x1=x3;x3=t;} *p1=x1;*p2=x3; return(n); } gold(float *p) { float a,b,x1,x2,f1,f2; int n=0; finding(&a,&b); do {x1=a+0.382*(b-a); x2=a+0.618*(b-a);f1=f(x1);f2=f(x2);n=n+1; if(f1>f2) a=x1; else b=x2;} while((b-a)>e); *p=(x1+x2)/2;return(n); } main() { float a,b,x,min;int n1,n2; n1=finding(&a,&b); n2=gold(&x); min=f(x); printf("\n The area is %f to %f.",a,b); printf("\n The nunmber 1 is %d.",n1); printf("\n The min is %f and the result is %f.",x,min);

优化课程实验

实验一一维搜索方法实验 实验学时：2h 实验类型：常规 实验要求：必修 一、实验目的： 1.掌握确定搜索区间的进退法，一维搜索的黄金分割法、牛顿法（切线法）、二次插值法的基本思想及迭代过程。 2.掌握上述常用一维搜索方法的优缺点及程序编制的方法。 3.掌握采用一维优化方法求优时如何提高搜索效率，减少盲目性。 二、实验内容 1、任选实验以下内容之一，自编程序； 1) 用0.618法求函数f (x)=x(x+2)在区间[-3，5]中的极小点，要求精度为ε=0.01。 2) .用0.618法求函数f (x)=x2+x+2的近似极小点及近似极小值,以致[a， b]=[-1，3]，缩短的相对精度为ε=0.08。 3) 用牛顿法求函数 f (x)=x4-5x3-4x2-6x+60的极小点及极小值, 已知[a， b]=[3，4] ，要求精度为ε=0.01。 4) 用二次插值法求f (x)=x2+e–x的极小点及极小值, 已知[a，b]=[0，1] ，要求精度为ε=0.001。 5) 用二次插值法求f (x)=3x4-16x3+30x2-24x+8的极小点及极小值, 已知[a， b]=[0，3] ，要求精度为ε=0.001。 2、改变初始搜索区间或精度要求，观察程序运行结果及迭代次数的变化情况。 三、实验原理、方法和手段 一维搜索方法的内容包括搜索区间的确定和区间缩小两个内容，首先给定初始点，应用外推法确定一个高—低—高的单谷区间，在采用黄金分割法或插值法进行区间缩小，当区间缩小到收敛精度。 四、实验组织运行要求 本实验为上机实验，采用单人单机，集中授课形式。

五、实验条件 人均计算机一台，安装有C语言软件。 六、实验步骤 1. 实验课前，明确实验目的和要求，预习相关内容，应用选择的算法语言 编写程序； 2. 在C 语言环境下输入和调试程序； 3. 运行程序，分析结果的正确性； 4. 改变搜索区间，运行程序，观察结果和迭代次数的变化； 5. 改变收敛精度，观察结果和迭代次数的变化。 七、思考题 对黄金分割法和二次插值法的特点进行总结，具体使用时应如何选择？ 八、实验报告 1、写清上机实验的名称及要求。 2、所选优化方法的基本原理简述。 3、绘制程序框图。 4、程序中变量及参数说明。 5、运行结果分析。（要求输出迭代过程中搜索区间上下限、迭代次数、极小 点和极小值） #include #include double obfunc(double x) /*目标函数*/ { double ff; ff=pow(x,2)+9*x; return(ff); } void jts(double x0,double h0,double s[],int n,double a[],double b[]) /*进退法*/

程序实例-进退法

用进退法确定函数f(x)=x^2-6x+9的一优化搜索区间[a,b].设初始点x=0,初始步长h=0.用matlab程序 首先你的建立三个M函数文件，分别建立文件夹： （1）%typbound.m; function [lowbound,upbound]=typbound(x0,step0,startopint,searchdirection) step=step0; f0=tryobjfun(x0,startopint,searchdirection); x1=x0+step0; f1=tryobjfun(x1,startopint,searchdirection); if f1<=f0 while true step=2*step; x2=x1+step; f2=tryobjfun(x2,startopint,searchdirection); if f1<=f2 lowbound=x0; upbound=x2; break; else x0=x1; x1=x2; f0=f1; f1=f2; end end else while true step=2*step; x2=x0-step; f2=tryobjfun(x2,startopint,searchdirection); if f0<=f2 lowbound=x2; upbound=x1; break; else x1=x0; x0=x2; f1=f0; f0=f2; end end

end %(2)tryobjfun.m function f=tryobjfun(a,startopint,searchdirection) f=objfun(startopint+a.*searchdirection); %(3)确定函数，也就是你要确定搜索区间的目标函数，你也可以改，这仅是一个例子 function f=objfun(x) f=x(1)^3+x(2)^2-10*x(1)*x(2)+1; 在命令窗口调用建立的函数 %%0是初始探测点，0.01是初始探测步长，[0,0]是初始搜索点，[1,1]是方向>>[low,up]=typbound(0,0.01,[0,0],[1,1]) %%运行结果为 low = 2.550000000000000 up = 10.230000000000000 参考资料：吴祈宗，郑志勇，邓伟.运筹学与最优化matlab编程[M].北京：机械工业出版社，2009.

进退法

进退法 1. 算法原理 进退法是用来确定搜索区间（包含极小值点的区间）的算法，其理论依据是：()f x 为单谷函数（只有一个极值点），且[,]a b 为其极小值点的一个搜索区间，对于任意 12,[,]x x a b ∈，如果()()12f x f x <，则2[,]a x 为极小值的搜索区间， 如果()()12f x f x >，则1[,]x b 为极小值的搜索区间。 因此，在给定初始点0x ，及初始搜索步长h 的情况下，首先以初始步长向前搜索一步，计算()0f x h +。 （1） 如果()()00f x f x h <+ 则可知搜索区间为0[,]x x h + ，其中x 待求，为确定x ，后退一步计算0()f x h λ-，λ为缩小系数，且01λ<<，直接找到合适的*λ，使得()*00()f x h f x λ->，从而确定搜 索区间*00[,]x h x h λ-+。 （2） 如果()()00f x f x h >+ 则可知搜索区间为0[,]x x ，其中x 待求，为确定x ，前进一步计算0()f x h λ+，λ为放大系数，且1λ>，知道找到合适的*λ，使得()*00()f x h f x h λ+<+，从而确定搜索 区间*00[,]x x h λ+。 2. 算法步骤 用进退法求一维无约束问题min (),f x x R ∈的搜索区间（包含极小值点的区间）的基本算法步骤如下： （1） 给定初始点(0)x ，初始步长0h ，令0h h =，(1)(0)x x =，0k =； （2） 令(4)(1)x x h =+，置1k k =+； （3） 若()() (4)(1)f x f x <，则转步骤（4），否则转步骤（5）； （4） 令(2)(1)(1)(4),x x x x ==，()()(2)(1)f x f x =，()()(1)(4)f x f x =，令2h h =，

matlab进退法-切线法求极值

7、用进退法求极值： ()21036f x x x =--；a=，h=,ε=。 %建立函数f （x ）。 function y=f(x) if nargin==1 @ y=x^2-10*x-36; end end %建立用进退法求解极值の程序。 function y=jintui(a,h,e) " a=input('enter the value of a:'); h=input('enter the value of h:'); e=input('enter the value of e:'); m=1;n=1; x0=a; ` x1=x0+h; while abs(x1-x0)>e if f(x0)>f(x1) x0=x1; x1=x0+h*2^m; ：

m=m+1; else x1=x0; x0=x1-h/2^n; n=n+1; ( end end x=(x0+x1)/2; y=f(x); end | 运行结果如下： enter the value of a: enter the value of h: enter the value of e: ！ ans = 8、用切线法求极值： ()21635f x x x =-+； %建立原函数； 、

function y=f(x) if nargin==1 y=x^2-16*x+35; end end 【 %建立一阶导函数； function yd=fd(x) if nargin==1 yd=2*x-16; end 【 end %建立二阶导函数； function ydd=fdd(x) if nargin==1 ydd=2; ` end end %切线法求极值函数； %x0为给定の初值，n为计算次数； %f（x）、fd（x）、fdd（x）分别为原函数，一阶导函数，二阶导函数；| function [xj,yj]=qiexian(x0,n)